ПРОГРАММА  ГЕНЕРАЦИИ  ПСЕВДОСЛУЧАЙНОЙ  ПОСЛЕДОВАТЕЛЬНОСТИ  НА  ОСНОВЕ  ЛИНЕЙНОГО  КОНГРУЭНТНОГО  И  БИКВАДРАТНОГО  МЕТОДОВ

Курчатов  Михаил  Юрьевич

студент  4  курса, 

Московский  государственный  университет  информационных  технологий,  радиотехники  и  электроники,

РФ,  г.  Серпухов

E -mail:  kaaelss@gmail.com

Нурматова  Елена  Вячеславовна

канд.  техн.  наук,  зав.  кафедрой  «Приборы  и  информационные  технологии»,  доцент, 
Филиал  МИРЭА  в  г.  Серпухове ,

РФ,  г.  Серпухов

E-mail: 

THE  PROGRAM  OF  GENERATION  OF  PSEUDO-RANDOM  SEQUENCE  BASED  ON  A  LINEAR  CONGRUENT  AND  BIQUADRATIC  METHODS

Michael  Kurchatov

student  4  course,

Moscow  State  University  of  Information  Technologies,  Radio  Engineering  and  Electronics, 
Russia,   Serpukhov

Elena  Nurmatova

candidate  of  Science,  head  of  the  department  "Devices  and  Information  Technologies",
Moscow  State  University  of  Information  Technologies,  Radio  Engineering  and  Electronics, 
Russia,  Serpukhov

АННОТАЦИЯ

В  данной  работе  рассматривается  вопрос  построения  генераторов  псевдослучайных  чисел,  в  частности  на  основе  линейно-конгруэнтного  и  биквадратного  метода.  Показан  практический  результат  реализации  данных  методов  в  виде  интегрированного  программного  приложения.

ABSTRACT

In  this  paper  we  discuss  the  construction  of  pseudorandom  number  generators,  in  particular  through  the  linear  congruential  method  and  biquadratic.  Shows  a  practical  result  of  the  implementation  of  these  methods  in  the  form  of  an  integrated  software  application.

Ключевые  слова:  информационная  безопасность;  генераторы  псевдослучайных  чисел.

Keywords:  information  security;  pseudorandom  number  generators.

Информационная  безопасность  достаточно  часто  нуждается  в  генерации  случайных  чисел,  которые  по  большей  своей  части  являются  одной  из  преград  между  злоумышленниками  и  информацией. 

Существует  два  типа  случайных  чисел  —  случайные  числа  (true  random  numbers)  и  псевдослучайные  числа  (pseudorandom  numbers)  с  определенными  свойствами,  позволяющими  использовать  их  в  криптографии.  Отличие  случайных  и  псевдослучайных  последовательностей  заключается  в  том,  что,  узнав  часть  случайного  числа,  нельзя  точно  предугадать  следующие  комбинации,  а  псевдослучайные  числа  можно  рассчитать  по  заданному  алгоритму.  И  тут  появляется  вопрос,  зачем  же  нам  нужны  генераторы  псевдослучайных  чисел,  если  есть  генераторы  случайных  чисел?

  Основным  достоинством  является  псевдослучайность  числа,  генератор  псевдослучайного  числа  (ГПСЧ)  требует  начальное  порождающее  число  для  генерации  последовательности,  что  открывает  возможности  как  и  для  человека  заинтересованного  в  защите  информации,  так  и  для  злоумышленника. 

При  построения  псевдослучайной  последовательности  необходимо  уделять  внимание  их  криптостойкости,  а  именно:  прохождение  статистических  тестов  на  случайность  и  сохранение  надежности  при  раскрытии  части  их  порождающего  или  текущего  значения  в  последовательности  криптоаналитиком  [2].

На  данный  момент  ГПСЧ  используются  для  генерации  SSL  и  других  сертификатах.

Приведем  краткую  характеристику  линейно-конгруэнтного  и  биквадратного  методов.

Линейный  конгруэнтный  (далее  ЛК)  метод  заключается  в  расчёте  некоторой  цикличной  функции  вида  [1]:

  (1)

…

где:    —  часть  цифрового  ключа;

  —  порождающее  число;

a,b,c  —  некоторые  целочисленные  коэффициенты.

Важно  знать  что    формально  является  ограничителем,  период  не  может  иметь  больше    элементов.  Сам  по  себе  метод  не  является  криптографически  стойким,  поэтому  его  нельзя  использовать  без  дополнительных  решений  для  защиты  в  информационной  безопасности.  Вся  опасность  использования  ЛК  метода  заключается  в  том,  что  доходя  до  определённой  точки  последовательность  начинает  повторяться,  поэтому  в  ключах  используют  только  уникальную  часть  цифрового  кода  (без  повторяющихся  элементов).  Возможно  самым  главным  достоинством  является  простота  метода  и  его  малая  требовательность  к  ресурсам  системы.  Вне  криптографии  метод  достаточно  неплохо  работает  на  различных  малых  системах,  например  игровых  консолях  (ведь  кол-во  памяти  серьезно  ограничено).

Теперь  о  Биквадратном  (далее  БК)  методе,  основанный  на  последовательном  возведении  в  квадрат  числовых  данных  с  чётной  разрядностью,  начиная  с  порождающего  значения  t₀.

Этот  метод  так  же  требует  сравнительно  небольшое  количество  средств  ЭВМ  для  работы,  но  и  имеет  существенную  проблему,  связанную  с  цикличностью  результата.  В  криптографии  этот  метод  можно  использовать  с  дополнительными  средствами,  усложняющими  поиск  порождающего  значения  (ведь  узнав  порождающее  число,  или  строку,  злоумышленник  сможет  без  проблем  вычислить  и  всю  последовательность).

Для  наглядности  есть  конкретная  программная  реализация  в  VB.net,  осуществляющая  генерацию  последовательности  этими  методами.

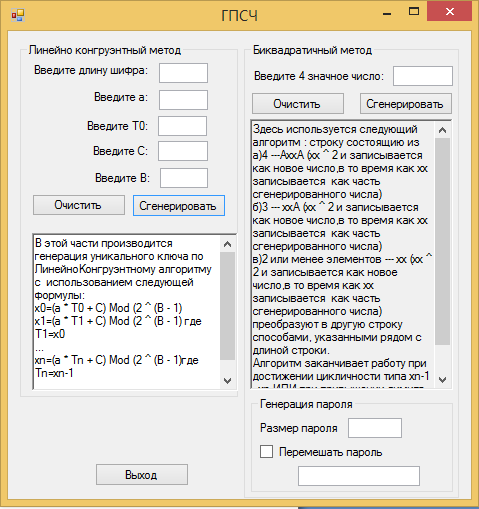
Рисунок  1.  Главная  форма  приложения  ГПСЧ

Ключ,  сгенерированный  с  помощью  БК  метода  можно  с  легкостью  перевести  в  ASCII  код  для  дальнейшего  использования,  например  в  качестве  пароля  \  ключа  для  чего  либо.  Важно  учитывать  что  ASCII  имеет  отображаемые  символы  начиная  с  №  32  (пробел),  поэтому  комбинация  01  сгенерированная  с  помощью  БК  метода  будет  переведена  в  ASCII  символ  №  33  (т.  е.  «!»),  помимо  этого  в  программе  имеется  возможность  перемешивания  пароля  с  помощью  алгоритма,  который  базируется  на  имеющихся  в  VB.net  средствах.

Программа  работает  следующим  образом:  в  поля  вводятся  начальные  значения,  в  случае  если  генерация  пароля  осуществляется  в  БК  методе  так  же  вводят  размер  пароля  и  согласие  на  перемешивание  пароля,  после  чего  нажимается  кнопка  «Сгенерировать»  и  в  нижнем  поле  программы  отобразится  пароль  для  копирования.  Если  флаг  «Перемешать  пароль»  не  убрать  и  ввести  новый  набор  данных  с  последующим  нажатием  кнопки  «Сгенерировать»  в  строчку  с  паролем  добавится  ещё  одна  последовательность,  таким  образом  можно  создать  композитный  пароль.

Подводя  итог,  можно  отметить  простоту  данных  методов  в  целом  (требуют  мало  ресурсов  ЭВМ,  достаточно  просты  в  расчётах)  и  основной  из  недостатков  —  легкость  в  предугадывании  последовательности  при  наличии  одного  из  параметров.  Несмотря  на  это  методы  применяются  (хоть  и  редко,  осторожно,  и  с  использованием  дополнительных  средств  защиты)  в  криптографии  и  достаточно  успешно  в  других  сферах  (в  игровых  консолях  и  других  малых  устройствах).

Список  литературы:

1.НОУ  ИНТУИТ  —  К2.Генерация  псевдослучайных  чисел,  линейно  конгруэнтный  метод.  [“лектронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.intuit.ru/studies/courses/553/409/lecture/17868  (дата  обращения  15.02.2015).

2.Хоффман  Дж.  Современные  методы  защиты  информации.  М.,  Советское  радио,  1980.  —  263  с.