Статья опубликована в рамках: LV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 24 февраля 2016 г.)
Наука: Технические науки
Секция: Энергетика и энергетические техника и технологии
Скачать книгу(-и): Сборник статей конференции
дипломов
ПРАКТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА ТОКОВ КОРОТКОГО ЗАМЫКАНИЯ В ЭЭС ПРИ СЛОЖНЫХ ВИДАХ ЗАМЫКАНИЙ С ИСПОЛЬЗОВАНИЕМ ФАЗНЫХ КООРДИНАТ
PRACTICAL METHOD OF CALCULATION OF SHORT CIRCUIT IN THE POWER SYSTEM UNDER DIFFICULT TYPES OF FAULT WITH PHASE COORDINATES
Alexey Osak
researcher, Melentiev Energy Systems Institute of Siberian Branch of the Russian Academy of Science (ESI SB RAS),
РФ, Irkutsk
АННОТАЦИЯ
Для выполнения расчетов токов короткого замыкания (ТКЗ) при сложных видах повреждений и несимметрии элементов сети целесообразно использовать метод фазных координат. В статье представлена методика расчета ТКЗ в фазных координатах в матричном виде и даны рекомендации по определению параметров схемы замещения для практических задач. Данная методика с 1998 года используется в лабораторных и научно исследовательских работах в Иркутском государственном техническом университете [2; 3], которая здесь уточнена в части задания трансформаторных ветвей в первой матрице инциденций. В ИСЭМ СО РАН [11] данная методика была дополнена учетом предшествующего аварии режима. Появление современных математических программных пакетов позволяет широко использовать данную методику для расчета ТКЗ в фазных координатах без использования специализированного программного обеспечения.
ABSTRACT
To perform the calculation of short circuit current in complex forms of fault, and the asymmetry of grid elements it is expedient to use the method of phase coordinates. The method of calculating the short-circuit current in phase coordinates in the matrix form. The recommendations for the definition of equivalent circuit parameters for practical works. This method is used since 1998 in laboratory and scientific research works in the Irkutsk State Technical University [2; 3], which has been added of the calculation of transformer branch in a first incidence matrix. In the ESI SB RAS [11], this method has been added taking into account the previous regime of the accident. The advent of modern mathematical software packages allows extensive use of this method to calculate the short-circuit current in phase coordinates without the use of specialized software.
Ключевые слова: токи короткого замыкания; фазные координаты; ЭЭС.
Keywords: current of short circuit; phase coordinates; power systems.
Задача расчета токов короткого замыкания (ТКЗ) является одной из типовых задач расчета режимов электроэнергетических систем (ЭЭС), которая необходима как для проектирования, так и для эксплуатации. Задача расчета ТКЗ применяется для выбора характеристик первичного и вторичного оборудования, расчета уставок устройств релейной защиты и автоматики (РЗА), проверки селективности РЗА, разбора и анализа фактических коротких замыканий (КЗ) и определения места повреждения (ОМП).
Для решения задачи расчета ТКЗ широко применяются промышленные программные комплексы отечественной и зарубежной разработки, такие как: АРМ СРЗА (г. Новосибирск), блок RastrKZ в составе RastrWin (г. Екатеринбург), EnergyCS ТКЗ (г. Москва), блок ТКЗ в составе ПВК АНАРЭС (г. Иркутск) [11].
В тоже время имеется ряд случаев, когда расчет ТКЗ на промышленных программных комплексах приводит к большим трудностям. К таким случаям можно отнести [9, с. 110; 12, с. 29]: сложные виды повреждений (многократные КЗ, КЗ между проводниками разных классов напряжения, сочетания КЗ и обрывов проводов и др.) или несимметрию нескольких элементов ЭЭС (неучет которой для конкретной практической задачи является неприемлемым). В этих случаях расчет ТКЗ проще всего выполнять с использованием фазных координат (ФК).
Метод ФК [9, с. 182] – это метод представления схемы замещения ЭЭС в пофазной постановке, а не в виде параметров схемы замещения прямой, обратной и нулевой последовательности как это осуществляется в широко применяемом методе симметричных составляющих (СС). При этом в ФК количество рассматриваемых фаз и схемы пофазного соединения всех элементов сети соответствуют фактическим схемам электроустановок (1 или 3 фазы, наличие или отсутствие нулевого провода и заземления нейтрали, наличие грозотроссов и их заземление). Продольные и поперечные сопротивления каждого элемента сети, а также взаимоиндукция между фазами и между элементами задается для каждой фазы отдельно [12, с. 248]. Вышеуказанные свойства ФК как раз и позволяют легко решать задачи расчета ТКЗ при сложных видах повреждений и несимметрии элементов сети.
Метод расчета режимов ЭЭС в ФК напрямую вытекает из расчета электрических цепей по законам Ома и Кирхгофа. Поэтому метод ФК известен уже более века. Но по сравнению с методом расчета в СС (при общепринятом допущении о симметричности элементов электрической сети матрицы сопротивлений в СС диагональные) метод ФК существенно более требователен к вычислительным ресурсам, потому что матрицы сопротивлений электрической сети в ФК не являются диагональными. Поэтому до появления высокопроизводительной вычислительной техники метод ФК не имел широкого применения для расчета режимов ЭЭС, в т. ч. для расчета ТКЗ.
С середины 1990-х годов уровень развития персональных компьютеров достиг уровня (по быстродействию и объему оперативной памяти), при котором применение метода ФК стало целесообразным. Имеется большое число публикаций на тему применения ФК для расчета различных режимов ЭЭС [1–9; 11–12], в т. ч. для расчета ТКЗ [9; 11–12].
В настоящее время широкое распространение получили универсальные математические программные комплексы (программные пакеты), позволяющие решать математические задачи различной сложности, в том числе задачи расчета режимов ЭЭС. Например:
- коммерческие: MATLAB, Mathcad, Mathematica;
- свободные: Scilab, GNU Octave, FreeMat.
Появление вышеуказанных универсальных математических программных комплексов позволяет качественно повысить доступность метода ФК для практических расчетов.
В настоящей статье представлена математическая постановка задачи расчета ТКЗ в ФК, которая может быть реализована в любом из универсальных математических пакетов или на языке программирования высокого уровня.
В ряде работ для выполнения расчетов режимов в ФК предлагаются достаточно сложные и индивидуальные алгоритмы формирования матрицы узловых потенциалов для разных элементов сети [12, с. 248; 9, с. 183; 7, с. 28]. Такой подход справедлив и работоспособен, но существенно усложняет алгоритм формирования схемы большой размерности. Используя современные математические пакеты или современные математические библиотеки для работы с матрицами и комплексными числами можно многие практические расчеты ТКЗ выполнять без каких-либо специальных и сложных алгоритмов, если не требуется учет индивидуальных особенностей отдельных элементов сети. Ниже излагается такая методика расчета ТКЗ в ФК в матричном виде.
Схема замещения для расчета ТКЗ в ФК.
Для расчета режима в ФК составляется схема замещения ЭЭС в пофазной (в 3-х фазной) постановке в виде графа сети (узлов и ветвей), топология которого может быть описана в матричном виде первой матрицей инциденций ![]() [10, с. 37].
[10, с. 37].
![]() представляет собой матрицу, каждая строка которой соответствует одному из узлов, а каждый столбец одной из ветвей. В ячейках матрицы записывается «0» – если ветвь не связана с узлом, «+1» – если узел является началом обычной ветви, «-1» – если узел является концом ветви. Для трансформаторных ветвей вместо «±1» со стороны узла низкого напряжения нужно записывать
представляет собой матрицу, каждая строка которой соответствует одному из узлов, а каждый столбец одной из ветвей. В ячейках матрицы записывается «0» – если ветвь не связана с узлом, «+1» – если узел является началом обычной ветви, «-1» – если узел является концом ветви. Для трансформаторных ветвей вместо «±1» со стороны узла низкого напряжения нужно записывать ![]() (где
(где ![]() ), знак «+» или «-» указывается как и для обычных ветвей. Каждый столбец матрицы может содержать только одно положительное число («+1» или «
), знак «+» или «-» указывается как и для обычных ветвей. Каждый столбец матрицы может содержать только одно положительное число («+1» или «![]() ») и одно отрицательное («-1» или «
») и одно отрицательное («-1» или «![]() »).
»).
В расчетах в ФК базисным узлом предпочтительно считать узел «земля», потенциал которого равен нулю, соответственно напряжение узла будет равно фазному напряжению узла относительно земли. Строку матрицы ![]() , соответствующую базисному узлу нужно исключить (чтобы размерность матрицы соответствовала числу независимых узлов), а при необходимости эту строку всегда можно восстановить.
, соответствующую базисному узлу нужно исключить (чтобы размерность матрицы соответствовала числу независимых узлов), а при необходимости эту строку всегда можно восстановить.
Первую матрицу инциденций ![]() можно представить в виде блочной матрицы
можно представить в виде блочной матрицы ![]() , Где
, Где ![]() – первая матрица инциденций для дерева графа сети (квадратная матрица).
– первая матрица инциденций для дерева графа сети (квадратная матрица). ![]() – первая матрица инциденций для хорд.
– первая матрица инциденций для хорд.
Если требуется выполнять расчеты методом контурных токов, то необходимо составить вторую матрицу инциденций ![]() . Строки матрицы соответствуют независимым контурам, а столбцы ветвям. В ячейках матрицы записывается «0», если ветвь не входит в контур, «+1», если обход контура совпадает с направлением тока ветви, «-1», если не совпадает. Вторую матрицу инциденций
. Строки матрицы соответствуют независимым контурам, а столбцы ветвям. В ячейках матрицы записывается «0», если ветвь не входит в контур, «+1», если обход контура совпадает с направлением тока ветви, «-1», если не совпадает. Вторую матрицу инциденций ![]() [10, с. 43] также можно представить в виде блочной матрицы
[10, с. 43] также можно представить в виде блочной матрицы ![]() , где
, где ![]() – соответствует ветвям дерева графа сети, а
– соответствует ветвям дерева графа сети, а ![]() – соответствует ветвям-хордам (квадратная матрица). Если выбирать независимые контуры таким образом, чтобы каждая хорда входила только в один контур, и направление тока в хорде совпадало с направлением обхода контура, то можно получить матрицу
– соответствует ветвям-хордам (квадратная матрица). Если выбирать независимые контуры таким образом, чтобы каждая хорда входила только в один контур, и направление тока в хорде совпадало с направлением обхода контура, то можно получить матрицу ![]() – единичной, тогда матрицу
– единичной, тогда матрицу ![]() можно получить алгебраически
можно получить алгебраически ![]() .
.
Для расчета схемы в матричной форме необходимо вначале составить матрицы параметров схемы замещения: ![]() ,
, ![]() ,
, ![]() . Матрица ЭДС ветвей
. Матрица ЭДС ветвей ![]() является матрицей вектор-столбцом, содержащей в каждой ячейке значение ЭДС в комплексном виде соответствующей ветви, причем знак перед ЭДС ставится в соответствии со следующим правилом. Если направление ЭДС совпадает с направлением тока, то ставится знак «+», иначе «-» (принятое направление тока из начала в конец ветви). Матрица задающих токов узлов
является матрицей вектор-столбцом, содержащей в каждой ячейке значение ЭДС в комплексном виде соответствующей ветви, причем знак перед ЭДС ставится в соответствии со следующим правилом. Если направление ЭДС совпадает с направлением тока, то ставится знак «+», иначе «-» (принятое направление тока из начала в конец ветви). Матрица задающих токов узлов ![]() является матрицей вектор-столбцом, элементами которой являются задающие токи в комплексном виде соответствующих узлов, причем знак «+» ставится перед током, если он входит в узел, «-» – если выходит из узла. Матрица сопротивлений ветвей
является матрицей вектор-столбцом, элементами которой являются задающие токи в комплексном виде соответствующих узлов, причем знак «+» ставится перед током, если он входит в узел, «-» – если выходит из узла. Матрица сопротивлений ветвей ![]() является квадратной матрицей. В главной диагонали
является квадратной матрицей. В главной диагонали ![]() находятся значения собственных сопротивлений ветвей в комплексном виде со знаком «+». В недиагональных элементах находятся значения взаимных сопротивлений между ветвями. Причем знак «+» ставится при согласном включении, «-» при встречном. Можно использовать и другие варианты направления векторных величин, главное, чтобы была единая система направлений для всей схемы, с учетом знаков в системе уравнений. В нижеизложенной методике используется следующие матричные уравнения.
находятся значения собственных сопротивлений ветвей в комплексном виде со знаком «+». В недиагональных элементах находятся значения взаимных сопротивлений между ветвями. Причем знак «+» ставится при согласном включении, «-» при встречном. Можно использовать и другие варианты направления векторных величин, главное, чтобы была единая система направлений для всей схемы, с учетом знаков в системе уравнений. В нижеизложенной методике используется следующие матричные уравнения.
Первый закон Кирхгофа [10, с. 58]:
![]()
Второй закон Кирхгофа:
![]()
Закон Ома:
![]()
Расчет методом узловых потенциалов.
Матрица узловых проводимостей:
![]()
Уравнение узловых напряжений [10, с. 76]:
![]()
![]()
Выражение токов ветвей через узловые напряжения:
![]()
Падение напряжения в ветвях схемы находится по выражению:
![]()
Потери мощности в только одной i-ой ветви находятся по выражению:
![]()
Поток мощности в i-ой ветви со стороны j-ого узла (начало или конец ветви) определяется по выражению:
![]() ,
,
где: ![]() – напряжение j-ого узла относительно базисного.
– напряжение j-ого узла относительно базисного.
Расчет методом контурных токов.
Матрица контурных ЭДС:
![]()
Матрица контурных сопротивлений:
![]()
Уравнение контурных токов [10, с.74]:
![]()

Выражение токов ветвей через контурные токи:
![]()
Падения напряжения в ветвях, входящих в дерево схемы находится по выражению:
![]()
Напряжения в узлах схемы относительно базисного определяется по выражению:
![]()
Практические рекомендации по расчету ТКЗ.
Расчет ТКЗ в ФК можно выполнять как методом узловых потенциалов, так и методом контурных токов. Если схема замещения содержит ветви с нулевым сопротивлением (например, соответствующие выключателю), то при расчете методом узловых потенциалов матрицы проводимостей ветвей по выражению ![]() произойдет деление на ноль. Поэтому у такой ветви необходимо нулевое сопротивление заменять некоторой малой величиной, что может несколько снижать точность расчета. В методе контурных токов такая проблема отсутствует, если только не весь контур содержит ветви с нулевым сопротивлением. Если схема замещения содержит ветви с очень большим сопротивлением (соответствующие отключенной ветви или обрыву, когда считается режим нескольких несвязанных подсистем), то в методе контурных токов возможно снижение точности за счет погрешности математических операций, тогда лучше покажет себя метод узловых потенциалов.
произойдет деление на ноль. Поэтому у такой ветви необходимо нулевое сопротивление заменять некоторой малой величиной, что может несколько снижать точность расчета. В методе контурных токов такая проблема отсутствует, если только не весь контур содержит ветви с нулевым сопротивлением. Если схема замещения содержит ветви с очень большим сопротивлением (соответствующие отключенной ветви или обрыву, когда считается режим нескольких несвязанных подсистем), то в методе контурных токов возможно снижение точности за счет погрешности математических операций, тогда лучше покажет себя метод узловых потенциалов.
Составление матриц с параметрами схемы замещения для практических расчетов ТКЗ.
При наличии готовой расчетной схемы для расчета ТКЗ в любом из промышленных программных комплексов можно для решения практических задач получить параметры схемы замещения в ФК следующим образом. Вначале поэлементно выполняем преобразования матрицы с параметрами схемы замещения одного элемента сети в СС в матрицу с параметрами схемы замещения этого же элемента сети в ФК по следующим выражениям (обращая внимание на порядок расположения в матрицах параметров соответствующих последовательностей и фаз):
![]()
![]()
![]()
где:  ,
, ![]() ,
, ![]() – операторы поворота вектора.
– операторы поворота вектора.
Если имеются данные о взаимоиндукции нулевой последовательности между двумя или несколькими ЛЭП, то формируется матрица ![]() не для одной ЛЭП (размерностью 3х3), а сразу для нескольких ЛЭП (размерностью 6х6, 9х9 и т. д.), в соответствующих недиагональных элементах указывается сопротивление взаимоиндукции нулевой последовательности между соответствующими ЛЭП.
не для одной ЛЭП (размерностью 3х3), а сразу для нескольких ЛЭП (размерностью 6х6, 9х9 и т. д.), в соответствующих недиагональных элементах указывается сопротивление взаимоиндукции нулевой последовательности между соответствующими ЛЭП.
Далее формируется матрица параметров схемы замещения: ![]() ,
, ![]() ,
, ![]() , как блочные матрицы отдельных элементов сети.
, как блочные матрицы отдельных элементов сети.
После выполнения расчета в ФК можно параметры режима в ФК конкретного элемента преобразовать в параметры режима с СС:
![]()
![]()
Определение параметров схемы замещения генераторов для учета предшествующего режима при расчете ТКЗ.
При разборе аварий, анализе фактических коротких замыкания (КЗ), при проверке селективности РЗА, решении задачи определения места повреждения (ОМП) для повышения точности расчета ТКЗ требуется учет предшествующего аварии установившегося режима. Это позволяет уточнить модули и фазы ЭДС для генераторов. Если предшествующий режим был тяжелым, т. е. перетоки по отдельным электропередачам приближались к допустимым пределам по устойчивости, то влияние учета фаз ЭДС может существенно повлиять на результаты расчета ТКЗ.
Особенностью математического моделирования вращающихся электрических машин (в нашем случае синхронных генераторов) является то, что общепринятая система координат “d, q” повернута относительно общесхемной системы координат на угол ![]() , который является углом поворота ЭДС генератора и определяется предшествующим режимом.
, который является углом поворота ЭДС генератора и определяется предшествующим режимом.
Для неявнополюсных машин (турбогенераторов) все особенности учета предшествующего режима ограничиваются только определением параметров ЭДС генератора (прямой последовательности) по выражению:
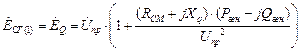
Активным сопротивлением генератора можно пренебречь, либо определить его через постоянную времени обмотки статора (справочный параметр):
![]()
Соответственно комплексное сопротивление прямой последовательности генератора для расчета ТКЗ:
![]()
Для обратной последовательности:
![]()
Обмотка статора синхронных генераторов обычно включается в звезду, причем нулевая точка в малых машинах изолирована, а в крупных машинах с целью выполнения релейной защиты от замыканий на землю заземляется через большое сопротивление. Поэтому токи нулевой последовательности либо отсутствуют, либо весьма невелики. Соответственно если в справочных данных отсутствуют параметры нулевой последовательности, то для перевода сопротивлений генератора в ФК можно сопротивление нулевой последовательности приближенно принять равным сопротивлению обратной последовательности.
Для явнополюсных машин (гидрогенераторов) при учете предшествующего режима необходимо учесть неравенство сверхпереходных сопротивлений по осям “d” и “q”.
Активное сопротивление гидрогенератора определяется через постоянную времени обмотки статора (справочный параметр):
![]()
Сопротивление гидрогенератора прямой последовательности в комплексном виде представить невозможно (из-за неравенства сверхпереходных сопротивлений по осям “d” и “q”), поэтому его нужно представлять в виде матрицы 2х2. Матрица сверхпереходных сопротивлений генератора в собственных осях генератора:
![]()
Матрица сверхпереходных сопротивлений генератора в общесхемной системе координат:
![]() ,
,
где: ![]() – матрица преобразования из системы “d, q” координат генератора в общесхемную систему координат:
– матрица преобразования из системы “d, q” координат генератора в общесхемную систему координат:
![]()
![]() ,
,
где: ![]() и
и ![]() определяется следующим образом:
определяется следующим образом:
![]()
![]() ,
,
где: ![]()
Соответственно в матричном виде ЭДС прямой последовательности для гидрогенератора:
![]()
Для обратной последовательности:
![]()

Список литературы:
1.Берман А.П. Расчет несимметричных режимов электрических систем с использованием фазных координат // Электричество. – 1985. – № 12. – С. 102–105.
2.Висящев А.Н., Осак А.Б. Расчет режимов электроэнергетических систем в фазных координатах // Конференция молодых специалистов электроэнергетики – 2000. Сборник докладов. – М.: НЦ ЭНАС, 2000. – С. 155–156.
3.Висящев А.Н., Домышев А.В., Осак А.Б., Пехотина И.Б. Расчет режимов тяговых сетей в фазных координатах // Повышение эффективности работы железнодорожного транспорта Сибири. Тезисы докладов научно-технической конференции. – Иркутск: ИрИИТ, 2000. – С. 79; 81.
4.Гусейнов А.М. Расчет в фазных координатах несимметричных установившихся режимов в сложных системах // Электричество. – 1989. – № 8. – С. 1–7.
5.Закарюкин В.П., Крюков А.В., Поклад Д.А. Программный комплекс расчета режимов систем тягового электроснабжения переменного тока в фазовых координатах // Повышение эффективности работы железнодорожного транспорта Сибири. – Иркутск: ИрИИТ, 2000. – С. 75–77.
6.Закарюкин В.П. Алгоритм расчета схемы замещения трехфазного трансформатора в фазовых координатах // Новые технологии управления и методы анализа электрических систем и систем тягового электроснабжения. – Иркутск. 2000. Вып. 1. – С. 31–38.
7.Закарюкин В.П., Крюков А.В. Сложнонесимметричные режимы электрических систем. – Иркутск: Изд-во Иркут. ун-та, 2005. – 273 с.
8.Закарюкин В.П., Крюков А.В. Методы совместного моделирования систем тягового и внешнего электроснабжения железных дорог переменного тока / под ред. А.В. Крюкова. – Иркутск: ИрГУПС, 2010. – 160 с.
9.Лосев С.Б., Чернин А.Б. Вычисление электрических величин в несимметричных режимах электрических систем. – М.: Энергоатомиздат, 1983. – 528 с.
10.Мельников Н.А. Матричный метод анализа электрических цепей – изд. 2-е, переработ. и доп. – М.: Энергия, 1972. – 231 с.
11.Осак А.Б. Блок расчета токов короткого замыкания и установившихся несимметричных режимов для ПВК АНАРЭС-2000 // Системные исследования в энергетике: Труды молодых ученых ИСЭМ СО РАН, Вып. 32. – Иркутск: ИСЭМ СО РАН, 2002. – С. 283–288.
12.Чернин А.Б., Лосев С.Б. Основы вычислений электрических величин для релейной защиты при сложных повреждениях в электрических системах. – М.: Энергия, 1971. – 434 с.
дипломов


Оставить комментарий