Статья опубликована в рамках: LV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 24 февраля 2016 г.)
Наука: Технические науки
Секция: Транспорт и связь, кораблестроение
Скачать книгу(-и): Сборник статей конференции
дипломов
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОДИКА ЧИСЛЕННОГО РАСЧЕТА ПРОЦЕССА ДВИЖЕНИЯ СЕДЕЛЬНОГО АВТОПОЕЗДА В ГОРНЫХ УСЛОВИЯХ ЭКСПЛУАТАЦИИ
MATHEMATICAL MODEL AND TECHNIQUE OF NUMERICAL CALCULATION OF PROCESS OF THE MOVEMENT OF THE SADDLE ROAD TRAIN IN MOUNTAIN SERVICE CONDITIONS
Orozbek Shatmanov
doctor of technical sciences, professor, Director of the Institute of transport and communications Kyrgyz State University of construction, transport and architecture named after N. Isanov,
Kyrgyzstan, Bishkek
Orozbek Omurov
associate professor at Kyrgyz State technical University named after I. Razzakov, Kyrgyzstan, Bishkek
Ulukbek Davlyatov
doctor of technical sciences, professor, head of Department “Automobile transport” of the Kyrgyz State technical University named after I. Razzakov,
Kyrgyzstan, Bishkek
АННОТАЦИЯ
Целью исследования является разработка методики расчета, позволяющей выбирать рациональный скоростной режим движения грузовых автомобилей с жидким грузом для конкретных дорожных условий.
Исходя из этого в статье рассмотрены основные характеристики автомобильной дороги Бишкек-Ош, обоснована актуальность разработки методики расчета, которая позволит выбирать рациональный скоростной режим движения грузовых автомобилей с жидким грузом, приведены математическая модель процесса движения седельного автопоезда, которая решается методами обратных задач динамики колесных машин, позволяющие определить параметры процесса движения с учётом смешения центра тяжести груза. Получена система из 28 дифференциальных уравнений. Эти уравнения совместно с начальными и граничными условиями представляют собой математическую модель процесса движения седельного автопоезда.
Для решения математической модели была разработана программа численного расчета с помощью программы MatLab Simulink и реализована на ПЭВМ. Рассчитанные числовые значения силы реакции на каждом колесе автопоезда позволят определить параметры устойчивого движения седельного автопоезда в горных условиях.
ABSTRACT
The aim of the study is to develop methodologies allowing to choose rational speed limit truck movements of liquid cargo for a specific road conditions. On this basis the article describes the main characteristics of the road Bishkek-Osh, the urgency of development of methods of calculation, which allows to choose a rational speed limit for freight vehicles with liquid cargo, the mathematical model of the process of movement of the saddle road train, which is solved by the methods of inverse problems of dynamics of wheeled vehicles, which allows to determine the parameters of the process of motion taking into account the mixing of the centre of gravity of the cargo. The resulting system of 28 differential equations. These equations together with initial and boundary conditions constitute the mathematical model of the process of the movement of the saddle road train. To solve mathematical model has been developed program of numerical calculation by using MatLab Simulink and implemented on the PC. The calculated numerical values of the reaction force on each wheel of the trailer will determine the parameters of a steady movement of the saddle road train in the mountains.
Ключевые слова: математическая модель, седельный автопоезд, скоростной режим, колесные машины, транспортный поток, автомобильная дорога, условия эксплуатации, режим движения.
Keywords: mathematical model, saddle road train, high-speed mode, wheel cars, transport stream, highway, service conditions, movement mode.
В Кыргызской Республике 65 % территории составляют горы, по которым осуществляются перевозки грузов. В частности, международная автомобильная дорога «Бишкек-Ош» является важной автомагистралью, соединяющей столицу республики с областями и соседними республиками – Узбекистаном, Таджикистаном и Казахстаном. На этой дороге интенсивность транспортного потока высока и в этих сложных высокогорных условиях перевозятся большие объемы грузов.
Так как, горные условия для эксплуатации грузовых автомобилей (автопоездов) являются крайне тяжелыми, очень важно знать их режим движения при изобилии крутых подъемов, спусков, поворотов и серпантинов [1, с. 152]. Особенно этот вопрос важен при перевозке жидких грузов (например, нефтепродуктов).
Всплескивание жидкого груза во время перевозок серьезно изменяет мгновенный центр тяжести автопоезда и тем самым, влияет на критическую скорость передвижения. Поэтому безопасность процесса перевозки во многом определяется правильным выбором скоростного режима автопоезда.
Протяженность автомобильной дороги Бишкек-Ош составляет 674 км, из них 348 км горные участки, а 246 км равнинной местности. Перевал «Тоо-Ашуу» находится на высоте 3500 м над уровнем моря. Наиболее сложным является участок дороги со 103–140-й километры, который проходит через перевал «Тоо-Ашуу». Данный участок осложнен тем, что 12 км перед вершиной перевала крутой подъем, связанный с преодолением 56 опасных серпантинов с малыми радиусами кривых в плане. Ширина проезжей части на этом участке дороги равна 8 м, а ширина обочины с каждой стороны по 2 м. Наименьший радиус кривых в плане 40 м, а наибольший продольный уклон составляет 83 промилле или 8,3 %.
На основании обобщения опыта эксплуатации и обзора теоретических исследований выдвинута гипотеза о возможности повышения эффективности перевозки жидких грузов за счет определения показателей безопасного и эффективного режима движения.
При анализе факторов, влияющих на режим движения, рассматривались факторы по эксплуатационным свойствам, внешние факторы и факторы по экономическим показателям.
Криволинейное движение автопоезда в горных условиях является превалирующим, так как движение даже на строго прямолинейных участках дорог сопровождается подъемами и поворотами управляемых колес для коррекции направления движения и объезда возникающих на пути препятствий. Более 50 % своего пробега автопоезд движется по дугам окружности радиуса от 40 м до 500 м. Характер криволинейного движения автопоезда зависит от его режима.
Достижение необходимых скоростей движения автопоездов определяется безопасными и эффективными параметрами режима движения за счёт максимального использования сцепных сил. Не учёт данных параметров при расчёте режима движения может привести к ситуации, когда автопоезд в экстремальных условиях может потерять устойчивость движения [2, с. 33].
Увеличение числа осей в пределах заданной базы приводит к снижению критической скорости. Уменьшает критическую скорость также увеличение массы и радиуса инерции автопоезда в горизонтальной плоскости. Также на устойчивость автопоезда большое влияние оказывают удельные величины реакций, действующие на колеса в плоскости движения, а, следовательно, и их составляющие – продольная и боковая реакции.
Исходя из этого, нами разработана методика по обоснованию режима движения автопоезда с максимальной скоростью движения, при котором обеспечивается устойчивое и безопасное движение.
Методика основывается на математической модели седельного автопоезда, которая решается методами обратных задач динамики колесных машин, позволяющих определить параметры процесса движения с учётом смешения центра тяжести груза. Седельный автопоезд рассматривается как сложная динамическая система, состоящая из двух подсистем, тягача и прицепа (рис. 1).

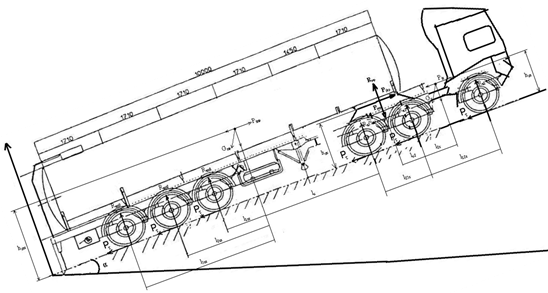

Рисунок 1. Схема сил, действующих на автопоезд, состоящий из тягача MAN TG SWW и полуприцепа – цистерны ФРЮЕХАУФ-TF34T13RBA
Используя проекции сил на оси координат и моментов сил относительно осей, нами получена система уравнений для полуприцепа и тягача. В результате решения определяются три силы реакции колес при предположении, что силы реакции левых и правых колес осей неодинаковы, сила реакции сцепного устройства и сила инерции.
Для полуприцепа
 1)
1)
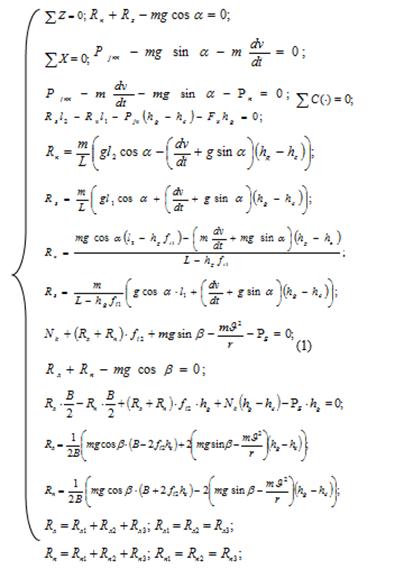
Для тягача

 2)
2)
где: Rл, Rп – силы реакции колес; Rк – сила реакции сцепного устройства; Nк – боковая сила реакции сцепного устройства; Рjкр – продольная сила инерции, действующая на сцепное устройство; mп – полная масса полуприцепа и mт – полная масса тягача; 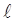
– расстояние между силами и осями; h – высота центра тяжести; v – скорость автопоезда;
 – угол подъема; r-радиус поворота;
– угол подъема; r-радиус поворота;  – угол поперечного уклона дороги; а1 – расстояние от центра массы тягача до переднего моста; а2 – расстояние от центра массы тягача до заднего моста; l0 – расстояние от центра массы тягача до сцепного устройства; h – высота центра тяжести тягача; Bt – колея тягача№ g – ускорение свободного падения, g=9.8 м/с2; L – расстояние от заднего колеса полуприцепа до сцепного устройства; hg – высота центра тяжести полуприцепа; hc – высота сцепного устройства; l2 – расстояние от заднего колеса полуприцепа до центра тяжести полуприцепа; l1– расстояние от центра тяжести полуприцепа до сцепного устройства;
– угол поперечного уклона дороги; а1 – расстояние от центра массы тягача до переднего моста; а2 – расстояние от центра массы тягача до заднего моста; l0 – расстояние от центра массы тягача до сцепного устройства; h – высота центра тяжести тягача; Bt – колея тягача№ g – ускорение свободного падения, g=9.8 м/с2; L – расстояние от заднего колеса полуприцепа до сцепного устройства; hg – высота центра тяжести полуприцепа; hc – высота сцепного устройства; l2 – расстояние от заднего колеса полуприцепа до центра тяжести полуприцепа; l1– расстояние от центра тяжести полуприцепа до сцепного устройства;  – продольный угол дороги,
– продольный угол дороги,  =0.05 рад; B – колея полуприцепа; fi1– продолный коэффициент сцепления; fi1– поперечный коэффициент сцепления; dv/dt – линейное ускорение автопоезда; РБ – поперечное динамическое воздействие жидкого груза на стенки цистерны; Рп – продольное динамическое воздействие жидкого груза на стенки цистерны.
=0.05 рад; B – колея полуприцепа; fi1– продолный коэффициент сцепления; fi1– поперечный коэффициент сцепления; dv/dt – линейное ускорение автопоезда; РБ – поперечное динамическое воздействие жидкого груза на стенки цистерны; Рп – продольное динамическое воздействие жидкого груза на стенки цистерны.
Используя проекции сил на оси координат и моментов сил относительно осей, нами получена система из 28 дифференциальных уравнений. Эти уравнения совместно с начальными и граничными условиями представляют собой математическую модель процесса движения седельного автопоезда.
Для решения математической модели была разработана программа численного расчета с помощью программы MatLab Simulink и реализована на ПЭВМ. Рассчитанные числовые значения силы реакции на каждом колесе автопоезда позволят определить параметры устойчивого движения седельного автопоезда в горных условиях.
На рисунках (рис. 2–5) представлены примеры результатов решения уравнении разработанной математической модели.
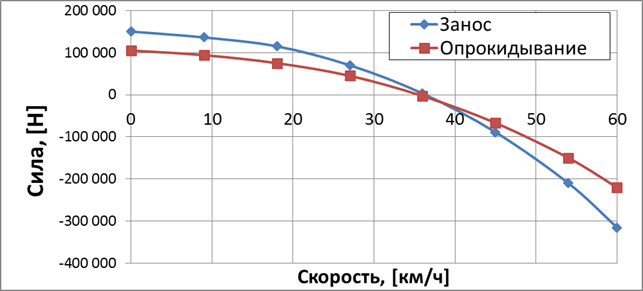

Рисунок 2. Суммарное воздействие способствующих и препятствующих сил опрокидыванию и заносу от скорости движения седельного автопоезда при радиусе поворота R=40 м, продольном уклоне 3 % и учете динамического воздействия жидкого груза

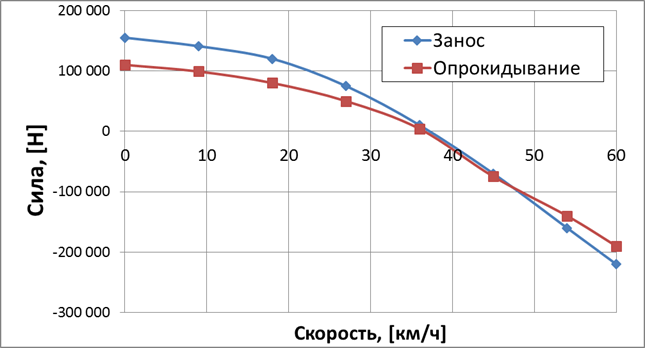
Рисунок 3. Суммарное воздействие способствующих и препятствующих сил опрокидыванию и заносу от скорости движения седельного автопоезда при радиусе поворота R=40 м, продольном уклоне 3 %, без учета динамического воздействия жидкого груза

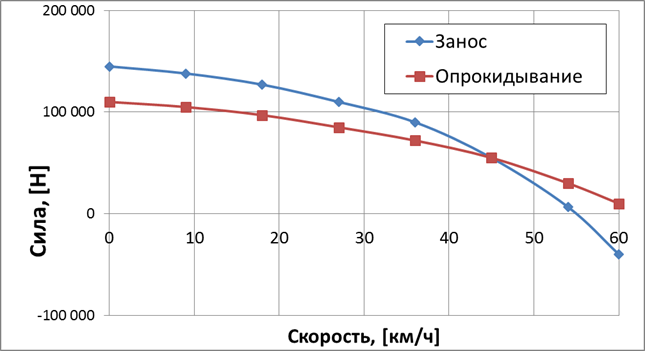
Рисунок 4. Соотношение способствующих и препятствующих сил опрокидыванию и заносу от скорости движения седельного автопоезда при радиусе поворота R=200 м, продольном уклоне 8 %, с учетом динамического воздействия жидкого груза


Рисунок 5. Соотношение способствующих и препятствующих сил опрокидыванию и заносу от скорости движения седельного автопоезда при радиусе поворота R=200 м, продольном уклоне 8 %, без учета динамического воздействия жидкого груза
Представленные графики показывают характер изменения суммарных сил, способствующих и препятствующих опрокидыванию, а также суммарных сил, способствующих и препятствующих заносу. По этим графикам можно определить критическую скорость (в точке пересечения с осью ординат при значении ноль), при которой начинается неустойчивое движение седельного автопоезда.
Список литературы:
- Бабков В.Ф. «Дорожные условия и безопаность движения». – М.: Т. 1993. – 271 с.
- Фаробин Я.Е. Теория движения специализированного подвижного состава / Я.Е. Фаробин, В.А. Овчаров, В.А. Кравцова. – Воронеж: ВГУ, 1981. – 160 с.
дипломов


Оставить комментарий