СОБСТВЕННЫЕ ЧАСТОТЫ КОЛЕБАНИЙ КОМПОЗИЦИОННЫХ ЛОПАСТЕЙ И ЛОПАТОК ТУРБОМАШИН

Байшагиров Хайрулла Жамбаевич

д-р техн. наук, руководитель лаборатории,

проф. Кокшетауского госуниверситета им. Ш. Уалиханова,

Республика Казахстан, г. Кокшетау

Е-mail: bayshagir@mail.ru

Ермаганбетова Сауле Каировна

соискатель, магистр естественных. наук,

преподаватель Кокшетауского госуниверситета им. Ш. Уалиханова,

Республика Казахстан, г. Кокшетау

Е-mail: sever_sk@mail.ru

SELF-RESONANT FREQUENCY OF COMPOSITIONAL IMPELLERS AND BLADES OF TURBO-MACHINES

Khayrulla Bayshagirov

doctor of Technical Sciences, Lab Supervisor,

Professor of Sh. Ualikhanov Kokshetau University,

Kazakhstan, Kokshetau

Saule Yermaganbetova

degree-seeking student, Master of Natural Science,

Lecturer of Sh. Ualikhanov Kokshetau University,

Kazakhstan, Kokshetau

АННОТАЦИЯ

Цель статьи заключается в определении спектра низших собственных частот колебаний ответственных композиционных изделий в турбомашинах. Задача о поперечных колебаниях пластин решалась методом Рица на основе энергетического принципа. Сравнение полученных численных результатов с опытными данными для стеклопластика даёт их удовлетворительное совпадение. При этом частоты колебаний лопастей ветротурбины находятся в пределах слышимых человеком диапазоне и не представляют опасности для его здоровья. Результаты можно использовать для оптимизации внутренней структуры материала с целью получения приемлемого уровня собственных частот элементов конструкции.

ABSTRACT

The purpose of the article is to determine the range of lower natural vibration frequencies of chargeable composite manufacturing in turbo machines. The problem of transverse vibrations of plates is solved by Ritz based on the energy principle. Comparison of obtained numerical results with experimental data for fiberglass gives them a satisfactory match. The frequencies of the oscillations of the wind turbine blades are within the range of human hearing and are not dangerous to his health. The results can be used to optimize the internal structure of the material in order to obtain acceptable levels of the self-resonant frequencies of the construction.

Ключевые слова: турбомашина, конструкция, колебания, лопатка, лопасть, ветроустановка, стеклопластик.

Keywords turbo machine, construction, oscillations, blade, impeller, wind turbine, glass-fiber material.

Среди требований, предъявляемых к ветроустановкам, особняком стоит вопрос недопущения ими излучения колебаний, вредных для живого организма. Они возникают из-за того, что обладающие большой линейной скоростью (при больших оборотах) периферийные сечения лопасти рассекают воздух с разряженными участками. Этот неравномерный по плотности участок – след от «уходящей» вперед предыдущей лопасти. Таким образом, возникают условия для изгибных колебаний тела в плоскости наименьшей жесткости. Угол атаки в сечениях меняется вдоль лопасти так, что наименьший наклон хорды к плоскости вращения приходится на концевые сечения. Это тоже благоприятствует возникновению поперечных колебаний, в особенности, для длинных лопастей. В связи с этим представляет интерес исследование собственных частот изгибных колебаний армированных пластин, имитирующих лопасть ветроустановки.

Задача расчета собственных частот и форм колебаний стержней, балок, закрученных рабочих лопаток с точки зрения однородной теории рассматривалась в литературе неоднократно. Основы расчета и методы достаточно подробно описаны в работах Бицено и Граммеля [5].

Колебания и волны в слоистых и композитных телах рассмотрены в работах Ван Фо Фы Г.А. [6], Ахенбаха Д.Ж. [1] и некоторых других, причем здесь использовались соотношения изотропной или анизотропной однородной теорий упругости.

Здесь изучается метод расчета армированной прямоугольной пластины при свободных колебаниях. Для определения собственных частот используются соотношения анизотропной квазиоднородной теории упругости [1; 8] и метод Ритца [9].

Пусть прямоугольная армированная пластина длины ℓ, толщины h и ширины 2b закреплена по краю х=0. Ось ох совпадает с осью симметрии пластины, ось оу направлена по закрепленному краю, т. е. 0≤х≤ℓ, – b ≤у≤ b, – h/2≤z≤h/2 (Рис. 1). Используем принцип Гамильтона [8], тогда справедливо равенство:

                                             (1)

Если предполагать, что существуют только нормальные колебания

w (х, у, t), то кинетическую энергию К можно представить в виде:

,              (2)

где: ρ – плотность тела, ρ= ρ^н V^н + ρ^м V^м, V– объем тела, S-сечение.

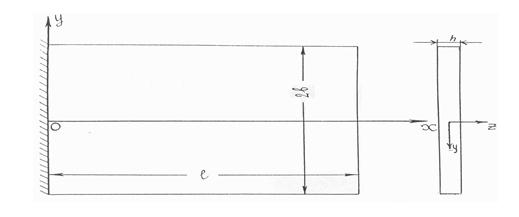
Рисунок 1. Армированная пластина прямоугольного сечения

Потенциальную энергию П для трансверсально-изотропной пластины в рамках квазиоднородной модели можно записать в виде [8]:

 (3)

Здесь Е₁ , Е₂, υ₁ , υ₂ – модули Юнга и коэффициенты Пуассона для главных направлений, совпадающих с направлениями осей ОХ и ОУ, G- модуль сдвига в плоскости XОY.

Полагаем, что существуют только периодические колебания с частотой ω, т. е.

                                         (4)

Если выбрать v (х, у) в виде ряда известных функций с произвольными коэффициентами А_i, то варьирование интеграла (1) сведется к дифференцированию его по этим неизвестным параметрам. Следуя работе [8], положим, что

                       (5)

Так как пластина закреплена лишь по краю х=0, естественно выбрать координатные функции X_m (х), У_n (у) как собственные функции консольной и свободной балок, соответственно. Тогда:

 (6)

Эта функция удовлетворяет граничным условиям:

;  (7)

В (6) =х/ℓ, а волновое число k_m=υ_m ℓ удовлетворяет характеристическому уравнению 1+ ch k_m cos k_m=0 и принимает значения [8], данные в таблице 1.

Таблица 1.

Значения волновых чисел

Примечание: в последнем столбце дана приближенная формула для m≥4.

При этом

                                    (8)

где: S- площадь поперечного сечения, E₁·I – изгибная жесткость. Балочные функции X_m(), являясь ортонормированными, удовлетворяют равенствам:

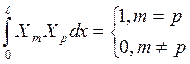
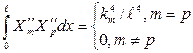 .        (9)

Из выражения (1) после преобразований получаем характеристическое уравнение, из которого следует удобная для конструкторов формула:

                                    (10)

позволяющая рассчитать технические частоты для изгибных стержневых форм колебаний (т. е. без продольных узловых линий).

Для сравнения с результатами эксперимента, проведенного для стеклопластика с приведенными ниже характеристиками, рассмотрим узкую прямоугольную пластину, размеры которой соответствуют компрессорной лопатке авиационного двигателя:

Е₁ =0,29 ·10⁵ Мпа, Е₂ =0,19 ·10⁵ Мпа, υ₁ =0,13; υ₂ =0,11

G =3,2 ·10³ Мпа, ρ=2,04 ·10³ кг/м³,

ℓ=0,12 м, h = 0,003 м, 2b=0,03 м.

Рисунок 2. Компрессорные лопатки из стеклопластика с «хвостовиком» для консольного закрепления

Значения экспериментальных и вычисленных технических частот ƒ_m (при m=1,2,3), помещенные в таблице 2, близки по своей величине. Сравнение их показывает, что низшие собственные частоты изгибных колебаний армированных узких пластин с погрешностью не более 5 % можно подсчитать по приближенной формуле (10). При m≥4 эта формула дает заметные погрешности, поэтому расчет надо вести, например, методом последовательных приближений [9].

Таблица 2.

Расчетные и экспериментальные собственные частоты

На основе гранта Комитета науки МОН РК [2] разработан и создан опытный образец стеклопластиковой ветроэнергетической установки с диффузором (ВЭУД).

Рисунок 3. Модельный прототип турбомашины ВЭУД и его ветроколесо с лопастями

 Используем приведенные выше характеристики стеклопластика и размеры для пластины, имитирующей лопасть первого [2] опытного образца ВЭУД (h=0,005 м; b=0,1 м; ℓ=0,38 м). Тогда по формуле (10) получим следующие значения собственных частот для низших форм колебаний:

f₁ = 20 Гц, f₂ = 130 Гц, f₃ = 350 Гц.

Лопасть модельного прототипа ВЭУД [3] была изготовлена на основе стеклоткани ТС–10 и эпоксидного связующего марки ЭДТ-10, т. е. Е₁= 0,5·10⁵МПа; ν₁=0,33; ν₂=0,29; ρ=2·10³кг/м³. Использовав эти характеристики, можно получить из формулы (10) следующий спектр собственных частот:

f₁ = 29 Гц, f₂ = 180 Гц, f₃ = 500 Гц.

Повышение значений этих трех низших частот на 38–45 процентов по сравнению с первым вариантом вызвано тем, что образец из стеклоткани ТС-10 обладает более высокими жесткостными характеристиками, чем образец из стеклопластика в первом варианте.

Спектры значений вычисленных собственных частот (20, 130, 350 Гц), (29, 180, 500 Гц) входят в диапазон слышимых человеком колебаний, поэтому не представляют опасности для его здоровья.

На вращающуюся лопасть действуют центробежные силы, растягивающие ее в продольном направлении. Как показали расчеты, они незначительно повышают собственные частоты низших форм колебаний [3].

При испытаниях ВЭУД в полевых условиях при температуре минус 33 градусов по Цельсию лишь в непосредственной близости от работающей ветротурбины был слышен соответствующий звук, напоминающий умеренный шум обычного бытового вентилятора [2; 3; 4].

Список литературы:

1.    Ахенбах Дж.Д. Колебания и волны в направленно-армированных композитах. // В кн.: Композиционные материалы. – М.: Мир, 1978. – С. 354–400; ил. – (Механика композиционных материалов: т. 2).

2.    Байшагиров Х.Ж., Каримбаев Т.Д., Петров Ю.А. и др. Разработка и создание композиционной ветроэлектрогенераторной установки с диффузором // отчет НИОКР. – Кокшетау, 2004. – № Госрегистрации 0105 РК 00008. – 91 с.

3.    Байшагиров Х.Ж., и др. Создание модельного прототипа композиционной ветроэнергетической установки с диффузором (ВЭУД) // Отчет о НИР. – Кокшетауский государственный университет им. Ш. Уалиханова. – Кокшетау, 2014. – С. 123–128. ГР 0112РК01562.

4.    Байшагиров Х.Ж. Разработка композиционных элементов конструкций и узлов турбомашин на основе классических и двухкомпонентной моделей упругой среды: диссерт. … докт. техн. наук. – Алматы, 2007 г.– 287 с. 

5.    Бицено К.Б., Граммель Р. Техническая динамика. // ГИТТЛ. – 1952. – Т. 11. – 290 с.

6.    Ван Фо Фы Г.А. Теория армированных пластиков. – Киев: Наукова Думка, 1971. – 231 с. 

7.    Карташов Г.Г. Влияние различных факторов на вибрационные характеристики лопаток из композитов. // Механика композиционных материалов – 1981. – № 3. – С. 486–493.

8.    Лейбензон Л.С. Вариационные методы решения задач теории упругости. – М.: Гостехиздат, 1973. – 287 с.

9.    Ritz. Theorie der Transversalschviqungen einer quadratischer Platte m freien Handern. Ann. d. Phys. (4). – 28. – 1909. – 306 р.