SPACE, TIME AND QUATERNIONS

Vladimir Korolev

candidate of Physical and Mathematical Sciences, assistant professor, Saint-Petersburg State University,

Russia, Saint-Petersburg

Viktor Novoselov

doctor of Physical and Mathematical Sciences, professor,

Saint-Petersburg State University,

Russia, Saint-Petersburg

Аннотация

Рассматриваются основные свойства кватернионов Гамильтона и возможное их применение в задачах аналитической и небесной механики или теории относительности.

Abstract

We consider the properties of the Hamilton quaternions and the possible application in problems of analytical and celestial mechanics, cosmology and theory of relativity.

Ключевые слова: кватернионы; аналитическая и небесная механика; преобразование пространства и времени.

Keywords: quaternions; analytical and celestial mechanics; transformations of space and time.

Пространство и свойства кватернионов.

В основах математики лежит понятие числа, которое позволяет описывать отношения изучаемых объектов к некоторому эталону. В процессе развития и совершенствования наук, описывающих окружающий нас мир, и усложнения математических конструкций появляются объекты, обладающие совершенно новыми свойствами. Первое обобщение понятия действительного числа получилось введением комплексных чисел с помощью мнимой единицы и правил алгебраических действий с упорядоченной парой разнородных элементов. Они оказались удобным математическим средством, позволяющим решать многие проблемы. Попытки дальнейшего обобщения привели к появлению и развитию гиперкомплексной системы и кватернионов [1; 2; 5; 13]. Оказалось, что из точек q = (а, b, c, d) четырехмерного пространства R⁴ можно построить числовую систему. Важная особенность кватернионов состоит в том, что их подмножеством можно считать вещественные числа (r, 0, 0, 0), комплексные числа (r, s, 0, 0) и векторы в трехмерном пространстве (0, x, y, z). Открытие кватернионов показало плодотворность абстрактных обобщений понятия число. Далее это привело к появлению новых понятий в алгебре, геометрии, физике и механике.

В 1843 году ирландский математик У.Р. Гамильтон (1805–1865) сделал доклад на заседании Академии наук, где в качестве обобщения комплексных чисел дал определение кватерниона в следующем виде [19]

                                                              (1)

Здесь – вещественные числа,  – символы для особых мнимых единиц, свойства которых определяются следующими равенствами

                                      (2)

                   (3)

Сначала Гамильтон придумал слово «вектор», которым мы стали активно пользоваться. Так он назвал кватернионы, у которых первая компонента равна нулю. Сейчас такие кватернионы принято называть чисто мнимыми. Так как чисто мнимые кватернионы образуют пространство размерности три, то Гамильтон решил, что его теория включает в себя всю механику. Скорости, силы и многие другие физические величины описывали тройками чисел.

Над кватернионами можно выполнять арифметические действия сложения и умножения на число, что позволяет объединять их в линейное арифметическое пространство R⁴ или векторное специальное пространство Q⁴. Базис этого пространства определяют набором вещественной и мнимых единиц 1, i, j, k, которые называют базисными кватернионами. Таблица умножения [2; 13] позволяет выполнять алгебраические операции. Для суммы двух кватернионов

 ,                         (4)

получают новый элемент пространства путем сложения всех компонент

.                    (5)

Произведение кватернионов (4) с учетом (2) и (3) можно вычислять по формуле

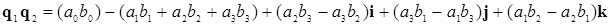(6)

При этом вещественная часть произведения кватернионов обладает свойством коммутативности (перестановки), хотя мнимые части подобным свойством не обладают. Вещественную единицу в векторной записи не используют.

Определяя умножение кватернионов, Гамильтон ввел две новые операции, каждая из которых в будущем оказалась очень полезной: векторное и скалярное умножения. В середине XIX века они были настоящим откровением.

Геометрическая интерпретация кватернионов привела к созданию векторной алгебры и анализа. Если  то сумма чисто мнимых кватернионов равносильна сумме векторов линейного пространства, где для элементов определены сложение и умножение на число. Вещественная часть для их произведения равна скалярному произведению со знаком минус, а мнимая эквивалентна векторному произведению.

Использование понятия линейной независимости (, если все коэффициенты равны нулю ) привело к появлению размерности и базиса линейного пространства. При создании декартовой прямоугольной системы координат для трехмерного пространства определили понятие проекции на оси и условие ортогональности элементов базиса (), что позволило рассматривать умножение векторов. Используя стандартные обозначения  для единичных ортогональных векторов базиса, которые определяют координатные оси, получили следующие свойства и обозначения

                   (7)

Для линейного пространства конечной размерности скалярное произведение векторов определяется выражением

,                                                     (8)

а векторное произведение не вводят. Векторное произведение для трехмерного пространства можно задавать в матричной форме

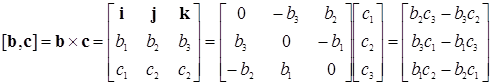       (9)

Следует различать для кватернионов  операции нормирования (вычисление нормы)

,                              (10)

и определение модуля (или длины) кватерниона

.                            (11)

Кватернионы единичной длины обладают свойством: при умножении двух единичных кватернионов получается снова единичный кватернион.

Сопряженный кватернион задается выражением

.                                      (12)

С его помощью определяют обратный (инверсный) кватернион

.               (13)

Для единичных кватернионов обратный совпадает с сопряженным.

Кватернионы являются обобщением комплексных чисел, которые состоят из двух связанных, но не взаимозаменяемых частей, а кватернионы – из четырех. Область применимости кватернионов оказалась меньше ожиданий, но они очень полезны, так как с их помощью можно описывать вращательное движения твердого тела в трехмерном пространстве [1; 4; 13; 18] и преобразование пространства-времени в теории относительности [16]. На основе работ по электромагнитной теории Максвелла и гипотезы Лоренца о неподвижном эфире Пуанкаре разработал математический аппарат [12] и получил обобщение принципа относительности Галилея для любых физических явлений. Это применяли и развивали Эйнштейн и многие другие для своих теорий [3; 17].

Кватернионы можно использовать для определения свойств векторов и действий над ними. В свою очередь геометрический смысл для суммы и произведения кватернионов можно пояснить с помощью действий сложения и умножения над векторами , которые представлены в виде массива или матрицы.

Например, систему линейных дифференциальных уравнений  можно записать в векторно-матричной форме для кватернионов

              .                 (14)

Решение системы уравнений можно представить в виде .

Иногда используют запись для кватернионов в виде суммы скалярной и векторной части q = t +r или рассматривают бивектор (t, r). При умножении чисто мнимых кватернионов используют запись . Здесь скобки (7) определяют скалярное и векторное умножение соответственно.

Необходимо различать множества точек аффинного или физического пространства и векторов, которые составлены из координат этих точек в виде тройки чисел (а, b, c), а также радиус-векторов . Это элементы разных пространств, которые предполагаются ассоциированными и могут как-бы передавать некоторые свойства. Кватернионы можно считать элементами арифметического пространства q = (а, b, c, d) ϵ R⁴ , для которого может быть определено скалярное произведение (8), чтобы получить евклидово пространство, или в стандартном виде (1) образовывать из них специальное пространство Q⁴, которое при умножении элементов сочетает свойства скалярного и векторного произведения.

Как показало появление тензорного анализа, который является основой современной физики, вектор от любого другого упорядоченного набора чисел отличается поведением при замене координат. Векторы Гамильтона вели себя неправильно, так как пространство было не изотропным (содержало разнородные элементы) и не годились на роль некоторых физически наблюдаемых объектов. Математически правильное описание кватернионов, а также их интерпретация были представлены в работе Родригеса. В начале XX века были открыты спиноры [1; 21], которые можно считать «правильным» обобщением векторов Гамильтона.

Для кватернионов нет такого наглядного геометрического представления, как для углов Эйлера, или простых выражений для матрицы преобразования координат при вращении тела (рис. 1) с неподвижной точкой.

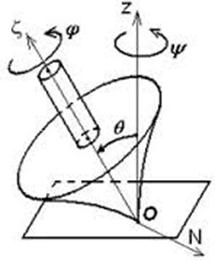
Рисунок 1. Вращение тела с неподвижной точкой и углы Эйлера

В отличие от углов Эйлера, которые любят в классической или небесной механике, такая интерпретация кватернионов лишена особенности и неоднозначности, которые определяются несколькими значениями параметров для углов Эйлера одновременно. Сейчас кватернионы используют, например, при компьютерном моделировании движения тел, а также в датчиках ориентации на самолетах. Основанные на кватернионах вычисления более устойчивы, если в начальных данных содержится небольшая ошибка. Кватернионы используются для описания вращательного движения в космических исследованиях [1; 10; 13] при организации ориентации спутников на орбите.

Определение вращения твердого тела.

Преимущество использования кватернионов зависит от конкретной задачи для представления вращения тела [4; 5; 9; 18]. Кватернион позволяет избавиться от накапливаемых ошибок, связанных с неточностью машинного представления чисел. Для того чтобы матрица вращения с использованием углов Эйлера после многократного перемножения на другие матрицы не накапливала ошибок округления, ее приходится нормировать или использовать поправки в процессе вычислений.

Можно рассмотреть задачу определения вращения твердого тела с использованием кватернионов (рис. 2). Скорость вращения тела удобно хранить в виде вектора, который совпадает по направлению с осью вращения и длина которого пропорциональна угловой скорости.

Рисунок 2. Поворот тела вокруг выбранной оси

Точное решение требует найти угол, на который тело повернулось за отведенное время. Основной операцией является создание кватерниона поворота из одного положения в другое по дуге окружности, образованной векторами с этими направлениями. Это кратчайший путь между точками на сфере. Можно использовать кватернион, вращающий на два таких угла. Он образован из векторного и скалярного произведений этих векторов.

Кватернионы единичной нормы предоставляют алгебраический способ определения вращения тела в трёхмерном пространстве. Связь между вращениями и кватернионами может быть показана через группу SO(3), которую называют пространством вращения [1; 9] евклидова пространства размерности три. Буква О обозначает ортогональность или сохранение расстояний (длины), а буква S – сохранение ориентации (или углов) при преобразовании. Это совокупность всех возможных поворотов сферы вокруг всевозможных осей.

В кватернионной форме можно записать поворот вокруг любой оси с вектором n единичной длины для любого вектора r, который задает положение точки тела. Необходимо умножить его слева на специальный кватернион q, а затем на обратный q^-1. Получаем [4; 5] следующее выражение

                                    (15)

для вектора, который получается поворотом на угол .

Матрицу поворота по единичному кватерниону  можно определить следующим правилом [13]

              .              (16)

Перемножив три кватерниона, задающих вращение вокруг базовых осей, можно получить выражение для кватерниона через углы Эйлера.

Кинематика точки в четырехмерном пространстве.

В теории относительности [3; 16; 17] используется новое обобщенное понятие «пространство-время», которое можно считать расширенным четырехмерным пространством R⁴ векторов q = (t, x, y, z) или соответствующих элементов q пространства кватернионов Q⁴. Вещественная часть в этом случае соответствует времени t, а мнимая часть определяет радиус-векторы r точек в физическом трехмерном пространстве.

Произвольное движение твердого тела представляет собой соединение двух простейших видов: поступательного движения вместе с началом координат подвижной системы, где находится центр масс тела или выбранный полюс, и вращения подвижной системы, связанной с телом, относительно начала. При переходе от одной системы координат Oxyz к другой предполагается, что момент времени t является инвариантной величиной. В классической механике событиям отвечает одинаковый промежуток времени и остается одинаковым расстояние между точками во всех системах отсчета. При этом предполагается, что имеется мгновенная информация о положении начала и конца вектора перемещения от начального положения до конечного. Для удобства исследования может оказаться полезным выполнять замену независимой переменной t вместе с преобразованием координат и рассматривать неусеченный кватернион

,                                                    (17)

где: множитель l – скалярный параметр, t имеет размерность времени. Такое расширение кинематики на кватернионы Q⁴ или гиперкомплексное пространство H используют для специальной теории относительности.

При этом в качестве инвариантной принимают скалярную часть произведения кватернионов для разности двух событий, которая равна

.                      (18)

Рассмотрим класс систем, измерения в которых выполняются с помощью процесса, имеющего постоянную скорость с во всех системах. Если в момент времени t₁ выходит сигнал и наблюдается в другой точке в момент времени t₂, то получим d = (l² – с²)(t₂ – t₁)². Допуская неинвариантность промежутка времени, следует принять l = с, то есть скорости света в вакууме.

Для простейших систем, имеющих движение с постоянными скоростями вдоль некоторого направления, которое можно принять за ось x, получим линейное преобразование

t₁ = b₁₁ t₂ +b₁₂ x₂, x₁ = b₂₁ t₂ + b₂₂ x₂, y₁=y₂, z₁=z₂ .                  (19)

Для точек с координатами x₁ = 0 имеем x₂ = v t₂, поэтому получим b₂₁ = – v b₂₂. При x₂ = ± с t₂ должно быть x₁ = ± с t₁. Тогда

t₁ = (b₁₁ ± b₁₂ с) t₂ , ± с t₁ = b₂₂ (–v ± с ) t₂ ,

b₁₁ ± b₁₂ с = – b₂₂ (± v с^-1 – 1), b₁₁ = b₂₂, b₁₂ = – b₂₂ v с^–2 .

Коэффициент b₂₂ в этом случае определяется из условия инвариантности в виде

                                                   (20)

В результате получается преобразование Лоренца для кватернионов в случае перехода к другой системе отсчета. Для близких событий составляющие векторов определяют дифференциалы этих величин, а затем дают формулы для проекций скорости и ускорения. При этом обнаруживается [12; 17; 20] отсутствие симметрии в продольном и поперечном направлениях относительно оси.

В процессе движения материальной точки изменяется количество движения при действии сил взаимодействия с другими телами. Ограниченность скорости распространения сигнала не влияет на результаты наблюдения в первой системе, так как здесь точка покоится. Скорость изменения количества движения определяет силу взаимодействия и дифференциальные уравнения

                                           (21)

Здесь m₀ называют массой покоя в отличии от массы движения m, что особенно заметно при больших скоростях v, сравнимых со скоростью света. Это порождает многие эффекты и особенности теории относительности в отличии от классической «натуральной философии» Ньютона [11; 12].

Кватернионы в космической динамике.

При развитии космических исследований в ХХ веке одной из основных задач была проблема построения оптимальных траекторий движения управляемых космических аппаратов [6–8; 10] в гравитационном поле в окрестности Земли или для межпланетных перелетов, а также управление вращением аппарата относительно центра масс [9] или стабилизация для сохранения заданной ориентации конструкции в пространстве с антеннами и солнечными батареями.

На активных участках полета работают реактивные двигатели, при которых происходит существенное изменение массы ракеты, которую считают материальной точкой [10]. В классической механике скалярный параметр m называют мерой инерции, считают постоянной, не замечают и даже стараются исключить его из уравнений Ньютона, когда вводят силовые поля или потенциальную энергию. Описывая движение материальной точки переменной массы на основе второго закона, мы должны учитывать дополнительное уравнение для расхода топлива, а к действующим активным силам  добавлять реактивные силы  с учетом управления, которое зависит от направления вектора тяги реактивных двигателей и секундного расхода . Это позволяет фактически вводить новый кватернион  и записывать уравнение динамики точки переменной массы

.                                          (22)

В качестве уравнения можно также использовать дополнительно другой кватернион q =. Здесь параметр h уже не является константой из интеграла энергии, а изменяется при работе двигателей. Параметр входит в правые части дополнительных уравнений, а его производная определяется текущим состоянием. Векторная часть кватерниона определяет количество движения точки .

Уравнения движения в центральном гравитационном поле имеют особенность, которая проявляется при сближении с притягивающим центром для сильно вытянутых эллиптических траекторий при аналитическом или численном приближенном решении [6]. Устранить особенности уравнений можно преобразованиями Сундмана для времени, заменой переменных Леви-Чивита для времени и координат в плоском случае, а в трехмерном пространстве получено специальное преобразование Кустаанхеймо–Штифеля (KS) с переходом в расширенное пространство и заменой времени [7; 14; 15]. Уравнения для описания и решения задач получаются в результате регуляризирующего преобразования при одновременной замене независимой переменной и других переменных  на новые  в виде

                       (23)

Это преобразование является обобщением или расширением преобразований кватернионов. Оно устраняет особенности в исходных уравнениях движения в центральном гравитационном поле и приводит систему дифференциальных уравнений в новых переменных к почти линейному виду в пространстве увеличенной размерности

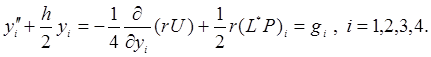                   (24)

Здесь r – модуль радиус-вектора, U – силовая функция учитываемых возмущений, P – непотенциальные силы, включая реактивную тягу двигателей на активных участках полета. Матрица преобразования L(y) и транспонированная матрица L^*(y) имеют вид

,                                 (25)

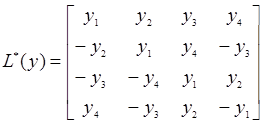.                                                     (26)

Дифференцирование в левой части системы уравнений (24) идет по новой независимой переменной, а параметр h играет роль медленно меняющейся частоты осциллятора и определяется текущим значением полной энергии, которая остается постоянной для невозмущенного движения и определяет тип траектории (эллипс, парабола или гипербола) с учетом возмущений

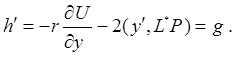                                       (27)

Неоднозначность KS-преобразования снимается дополнительным билинейным соотношением

                                       (28)

которое выделяет в расширенном конфигурационном пространстве сферический слой, соответствующий начальным данным. Правые части уравнений также удовлетворяют аналогичному (28) билинейному соотношению для любого вектора

                                        (29)

Четвертые компоненты векторов  и  в уравнениях (24) – (27) полагают равными нулю. Полученные уравнения можно привести к каноническому виду [7; 8] для специальных регулярных элементов.

Список литературы:

1. Арнольд В.И. Геометрия комплексных чисел, кватернионов и спинов. – М.: изд. МЦНМО, 2002. – 40 с.
2. Арнольд В.И. Геометрия сферических кривых и алгебра кватернионов. // Успехи математических наук. 1995, т. 50, вып. 1 (301). – С. 3–68.
3. Буфеев В.А. Кто и как создал теорию относительности. История создания и развития. – М., 2015. – 234 с.
4. Голубев Ю.Ф. Алгебра кватернионов в кинематике твердого тела // Препринты ИПМ им. М.В. Келдыша. 2013. № 39. – 23 с.
5. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. – М.: Наука, 1973. – 144 с.
6. Королев В.С. Оптимизация и вычисление траекторий методом возмущенных конических сечений // Вопросы механики и процессов управления. – Л.: изд. ЛГУ, 1988. – С. 67–72.
7. Королев В.С. Преобразование уравнений движения управляемых систем // Четвертые Поляховские чтения – СПб.: ВВМ, 2006. – С. 103–104.
8. Королев В.С., Новоселов В.С. Управление гамильтоновой системой с учетом возмущений // Инновации в науке. № 51-1. – С. 23–29.
9. Новоселов В.С., Кирпичников С.Н. Математические аспекты кинематики твердого тела. – Л.: Изд. ЛГУ, 1986. – 252 с.
10. Новоселов В.С., Королев В.С. Аналитическая механика управляемой системы. Учебное пособие. – СПб.: СПбГУ, 2005. – 298 с.
11. Ньютон И. Математические начала натуральной философии // Собр. трудов академика А.Н. Крылова / Перевод и комментарии А.Н. Крылова. – М. Наука. 1989. – 687 с.
12. Пуанкаре А. О науке. – М.: Наука, 1990. – 736 с.
13. Радыно Н.Я. Гиперкомплексные числа в задачах геометрии и алгебры. – Минск: БГУ, 2010. – 94 с.
14. Себехей В. Теория орбит. Ограниченная задача трех тел. – М.: Наука, 1982. – 655 с.
15. Штифель Е., Шейфеле Г. Линейная и регулярная небесная механика. – М.: Наука, 1975. – 304 с.
16. Эйнштейн А. Собрание сочинений в 4-х томах. – М.: Наука, 1967.
17. Юрьев А.Г. Четырехмерный мир без фактора времени // Успехи современного естествознания. – 2011, № 2. – С. 115–118.
18. Altmann S.L. Rotations, Quaternions, and Double Groups. – Oxford: Clarendon Press, 1986. – 317 p.
19. Hamilton W.R. On quaternions; or a new system of imaginaries in algebra. Phil. Mag., 25, 1844, Р. 489–495.
20. Maxwell J.C. Remarks on the mathematical classification of physical quantities, Proc. London Matla. SOC. 3 (1869), Р. 224–232.
21. Riesz M. Clifford Numbers and Spinors. Lecture Series, № 38, The Institute for Fluid Dynamics and Applied Mathematics, Maryland, 1958.