ЦЕНТРАЛЬНЫЙ  ЭЛЕМЕНТ  ЗВУКОВЫСОТНЫХ  СИСТЕМ:  МЕТОД  ГЕОМЕТРИЧЕСКОГО  МОДЕЛИРОВАНИЯ

Трубенок  Елена  Александровна

аспирант  Московской  государственной  консерватории  им.  П.И.  Чайковского,  г.  Москва

E-mail:  etrubenok@yandex.ru

CENTRAL  ELEMENT  OF  PITCH  SYSTEMS:  METHOD  OF  GEOMETRICAL  MODELING

Trubenok  Elena

postgraduate  student  of  Moscow  State  Conservatory  named  after  P.I.  Tchaikovsky,  Moscow

АННОТАЦИЯ

В  данной  статье  сделана  попытка  представить  таблицу  звуковысотных  систем  с  центральным  элементом  (термин  Ю.  Холопова)  как  ее  единицей  измерения,  который  является  тем  самым  неизменным,  что  объединяет  все  звуковысотные  системы  в  эволюции  музыкального  мышления.  Центральный  элемент  (ЦЭ),  выполняющий  в  звуковысотной  системе  функцию  тоники  или  центра,  имеет,  на  наш  взгляд,  геометрические  корни.  Нами  разработаны  модели  ЦЭ,  представляющие  собой  взаимодействие  окружностей.  Алгоритм  смены  моделей  ЦЭ  может  рассматриваться  как  одна  из  версий  неизменного  закона  эволюции  музыкального  мышления.

ABSTRACT

This  article  attempts  to  provide  a  table  of  pitch  systems  with  a  central  element  (Y.  Kholopov’s  term)  as  its  unit  of  measure,  which  is  the  very  same  thing  that  unites  all  pitch  system  in  the  evolution  of  musical  thought.  The  central  element  (CE)  that  performs  the  function  of  tonic  or  center  in  a  pitch  system  has,  in  our  view,  geometric  origins.  We  have  developed  models  of  CE,  representing  the  interaction  of  the  circles.  Algorithm  of  changes  of  CE  models  can  be  considered  as  a  version  of  the  law  of  constant  evolution  of  musical  thought.

Ключевые  слова:  центральный  элемент  звуковысотной  системы;  эволюция  музыкального  мышления;  окружность.

Keywords:  central  element  of  pitch  system;  the  evolution  of  musical  thought;  circumference.

Математический  подход  к  изучению  музыкальных  явлений  в  течение  многих  столетий  привлекал  внимание  ученых  и  не  потерял  актуальности  и  в  наше  время.  Ж.Ф.  Рамо  принадлежит  высказывание:  «Музыка  —  это  наука,  которая  должна  обладать  определенными  правилами,  эти  правила  должны  быть  выведены  из  неоспоримого  принципа,  а  этот  принцип  не  может  стать  нам  известным  без  помощи  математики»  [6,  с.  55]. 

Такой  позиции  придерживался  и  Ю.Н.  Холопов  (1932—2003),  распространяя  ее  на  область  эволюции  музыкального  мышления.  Он  писал,  что  «история  —  это  становящаяся  во  времени  логика.  И  как  обычно,  развертывание  логики  допускает  математическую  обработку»  [8,  с.  85]. 

Холопов  считал  одной  из  актуальных  проблем  современного  музыковедения  познание  музыкального  логоса  —  смысла  музыки  как  таковой,  совокупности  ее  неизменных  признаков,  который  можно  обнаружить  только  в  системе,  общей  картине  эволюции  музыкального  мышления. 

«Противоречивое  и  неравномерное  развитие  музыки»,  по  словам  Холопова,  укладывается  в  «математически  точную  «табличку»…  взаимодействием  изменяющегося  и  неизменного»  [8,  с.  85].  В  данной  статье  сделана  попытка  представить  такую  таблицу  звуковысотных  систем  с  ЦЭ  как  ее  единицей  измерения,  который  является  тем  самым  неизменным,  что  объединяет  все  звуковысотные  системы  в  эволюции  музыкального  мышления.

Центральный  элемент  (ЦЭ,  термин  Ю.Н.  Холопова)  —  одно  из  важнейших  понятий  теории  конструктивных  элементов,  разработанной  Холоповым.  Это  основной  конструктивный  элемент  звуковысотной  системы,  который  выполняет  в  ней  функцию  тоники  или  центра.  Его  структура  и  исторические  формы  различны  (аккорд,  полиаккорд,  одноголосный  ладовый  комплекс,  отдельный  звук,  звуковая  группа,  серия  и  т.  д.)  [см.  подробнее:  9,  10  и  др.  работы  Ю.Н.  Холопова]. 

Для  составления  таблицы  звуковысотных  систем  нами  были  разработаны  специальные  модели  ЦЭ,  который,  на  наш  взгляд,  имеет  геометрические  корни.  Модели  основаны  на  геометрическом  изображении  ЦЭ,  которое  представляет  собой  вариант  модели  квинтового  круга,  а  также  опирается  на  аналогичные  модели  диаграмм  Эйлера-Венна,  применяющихся  в  математической  теории  множеств,  и  изображение  химической  молекулы  бензола.

В  изложении  теории  Холопова  понятие  ЦЭ  дается  в  сочетании  с  некоторыми  другими  (исходный  элемент,  начальный  элемент,  главный,  контрастный).  Названия  «исходный»,  «начальный»,  «главный»,  «контрастный»  действительно  характеризуют  соответствующее  им  явление,  в  то  время  как  термин  «центральный  элемент»  указывает  лишь  на  некий  абстрактный  центр.  Попытаемся  конкретизировать  данное  понятие. 

Рисунок  1.  Кольцевая  замкнутость  хроматической  гаммы

Представим  хроматический  звукоряд  в  виде  круга.  Звукоряд  от  некоторого  звука,  пройдя  12  ступеней  хроматической  гаммы,  возвращается  к  тому  же  звуку  в  другой  октаве  (рис.  1).  Такая  кольцевая  замкнутость,  «встреча  звукоряда  с  самим  собой»  наблюдается  и  в  модели  квинтового  круга  (если  рассматривать  темперированный  строй  и  не  принимать  во  внимание  пифагорову  комму). 

Идея  закольцованности  модели  отразилась  не  только  в  музыке,  но  и  в  химии  —  при  создании  изображения  молекулы  бензола  (рис.  2).  Открытие  изображения  молекулы  этого  химического  соединения  (1865  г.)  принадлежит  немецкому  химику  Фридриху  Августу  Кекуле.  Ученый  представлял  себе  углеродные  цепи  в  виде  змей,  и  идея  цикличности  соединения  пришла  ему  во  сне,  когда  воображаемая  змея  укусила  себя  за  хвост  [1]. 

Рисунок  2.  Молекула  бензола  C₆H₆

Обращение  к  модели  круга  обусловлено  еще  и  тем,  что  круг  и  центр  —  понятия  хорошо  сопоставимые.  Центр  в  геометрии  —  точка,  равноудаленная  от  краев,  что  предполагает  обращение  к  замкнутой  геометрической  фигуре  («Окружностью  называется  фигура,  которая  состоит  из  всех  точек  плоскости,  равноудаленных  от  данной  точки  (называемой  центром  окружности)»  [3,  с.  26]).

Модель  ЦЭ  должна  быть  способна  к  отображению  всех  активных  измерений  в  звуковысотной  системе,  которую  эта  модель  представляет.  Современные  научные  теории  выдвигают  гипотезы  многомерного  пространства  (например,  теория  струн)  [4].  Данная  модель  отражает  множество  измерений  (мелодия,  гармония,  сонорика  и  др.)  с  особой  ведущей  единицей  в  каждом  из  них. 

Модель  ЦЭ,  состоящая  из  одного  круга,  изображает  только  одно  измерение  (горизонталь).  Система  трех  измерений  представлена  на  рисунке  3. 

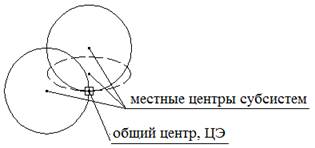
Рисунок  3.  Система  трех  измерений

В  каждом  измерении,  или  субсистеме,  есть  свой,  местный  центр,  но  в  то  же  время  все  три  измерения  соприкасаются  в  одной  точке  —  общем  центре.  Если  попытаться  изобразить  множество  измерений  и  во  всех  направлениях  от  общей  точки  построить  равные  окружности,  то  эта  точка  действительно  оказывается  центром  сферы  [7],  ее  ЦЭ  (рис.  4). 

Рисунок  4.  ЦЭ  как  центр  сферы

Окружности  в  каждой  модели  системы  могут  соприкасаться  не  только  в  одной  точке,  но  и  накладываться  друг  на  друга  в  разной  степени  вплоть  до  полного  совпадения,  а  также  могут  не  соприкасаться  совсем.  Область  наложений  представляет  собой  ЦЭ-точку  в  первом  случае,  ЦЭ-область  —  во  втором,  ЦЭ-систему  —  в  третьем,  и  ЦЭ-обертон  —  в  четвертом  (табл.  1). 

Таблица  1.

Следует  особо  отметить  некоторую  долю  условности  четвертой  модели.  Так  как  единицей  измерения  ЦЭ  выбран  звук  и  он  обозначается  точкой,  обертон  как  феномен,  являющийся  частью  звука,  не  может  быть  выражен  геометрически.  Модель  не  контактирующих  между  собой  окружностей  не  указывает  на  отсутствие  ЦЭ,  но  говорит  о  выходе  в  область  обертонов. 

Данные  модели  пересечений  окружностей  заимствованы  из  графических  обозначений  множеств  в  высшей  математике.  Модель  ЦЭ-области  совпадает  с  графическим  обозначением  произведения  множеств  при  помощи  кругов  Эйлера,  который  ввел  в  математику  данное  обозначение  множеств  [см.  подробнее:  5,  11]  (рис.  5).

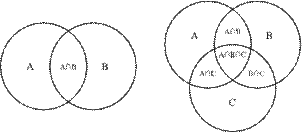
Рисунок  5.  Диаграмма  Эйлера-Венна  [12]

Таким  образом,  два  измерения  могут  взаимодействовать  только  четырьмя  способами.  Формирование  моделей  с  бóльшим  количеством  измерений  основано  на  тех  же  четырех  типах  взаимодействия. 

Присвоив  каждой  из  звуковысотных  систем  подходящую  ей  модель,  становится  возможным  сведение  их  в  таблицу  с  целью  выявить  закономерности  в  смене  звуковысотных  систем  в  эволюции  музыкального  мышления  (табл.  2). 

Таблица  2. 

Эволюция  звуковысотных  систем  (сквозь  призму  моделей  ЦЭ)

Таблица  2  имеет  три  строки  (или  периода);  в  каждой  из  них  представлены  звуковысотные  системы  с  тем  количеством  действующих  измерений,  которое  соответствует  номеру  периода.  В  каждом  периоде  (в  первом  из  них  —  в  неполном  виде)  представлен  алгоритм  движения  от  системы  к  системе:  от  ЦЭ-области  делается  шаг  к  ЦЭ-точке,  затем,  в  третьем  периоде,  продолжается  движение  в  том  же  направлении  —  к  ЦЭ-обертону,  и  завершается  каждый  период  скачком  в  обратном  направлении  —  к  ЦЭ-системе  (рис.  6).

Рисунок  6.  Алгоритм  движения  в  эволюции  музыкального  мышления

Трижды  повторенный,  хотя  и  с  изменениями,  алгоритм  движения,  показанный  на  рисунке  6,  образует  зигзагообразную  модель  эволюции  музыкального  мышления,  напоминающую  движение  маятника.

Возможно,  алгоритм  движения  между  ЦЭ,  обозначенный  выше  (см.  рис.  6),  составляет  неизменный  закон  эволюции  музыкального  мышления,  который  при  изменении  контекста  сохраняет  свою  сущность. 

  Таким  образом,  ряд  моделей  музыкальных  систем,  основанных  на  их  ЦЭ  и  расположенных  в  хронологическом  порядке,  показывает,  что  движение  между  ними  образует  цикл,  проявившийся  уже  трижды. 

Проведем  ряд  параллелей  с  периодической  таблицей  Д.  Менделеева.  Согласно  периодическому  закону,  сформулированному  Менделеевым,  «свойства  простых  веществ,  а  также  формы  и  свойства  соединений  простых  элементов  находятся  в  периодической  зависимости  от  величины  атомных  масс  элементов»  [2,  с.  46].  Вид  ЦЭ  также  зависит  от  положения  в  периоде  (это  определяет  тип  ЦЭ)  и  от  номера  периода  (это  определяет  количество  измерений  в  ЦЭ).  Как  и  в  системе  Менделеева,  столбцы  таблицы  (группы)  содержат  элементы  с  подобными  свойствами,  т.  е.  звуковысотные  системы  с  подобными  типами  ЦЭ. 

Подведем  итоги.  Обращение  к  геометрическим  аспектам  понятия  «центральный  элемент»  позволяет  расширить  сферу  влияния  термина,  возникшего  и  первоначально  употребляемого  преимущественно  в  области  гармонии.  ЦЭ  —  общее  явление  для  всех  систем  в  музыкальной  эволюции  и  подходящая  единица  для  составления  таблицы  систем  как  выражения  многомерного  музыкального  пространства.

Геометрический  смысл  ЦЭ  позволяет  представить  каждый  конкретный  центральный  элемент  как  абстрактную  модель,  основанную  на  определенном  сочетании  некоторого  количества  окружностей.  Многочисленные  модели  образуют  несколько  устойчивых  типов.  Алгоритм  смены  моделей  может  рассматриваться  как  одна  из  версий  неизменного  закона  эволюции  музыкального  мышления,  который  интересовал  Холопова  и  который,  по  словам  Рамо,  «не  может  стать  нам  известным  без  помощи  математики»  [6,  с.  55]. 

Данная  статья  является  дополнением  и  переработкой  ранней  публикации:  Трубенок  Е.  Геометрический  смысл  центрального  элемента  (ЦЭ)  //  Актуальные  проблемы  истории,  теории  и  методики  современного  музыкального  искусства  и  художественного  образования.  Сб.  науч.  трудов  ОГИИ.  Вып.  6  /  Гл.  ред.  Б.  П.  Хавторин,  сост.  и  науч.  ред.  В.  А.  Логинова.  —  Оренбург,  2009.  —  С.  179—192. 

Список  литературы:

1.Бензол.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://benzolsiroy.narod.ru/bc.html  (дата  обращения  4.04.2013).

2.Глинка  Н.Л.  Общая  химия  /  24-е  изд.,  испр.  —  Л.:  Химия,  1985.  —  702  с.

3.Гордин  Р.К..  Геометрия.  Планиметрия.  7—9  классы  /  Учебное  пособие.  —  3-е  изд.,  испр.  —  М.:  МЦНМО,  2006.  —  416  с.

4.Грин  Б.  Элегантная  Вселенная:  Суперструны,  скрытые  размерности  и  поиски  окончательной  теории.  —  М.:  Едиториал  УРСС,  2004.  —  286  c.

5.Круги  Эйлера.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://eileracrugi.narod.ru/istoriya  (дата  обращения  4.04.2013).

6.Рамо  Ж.Ф.  «Traité  de  l’harmonie»  //  Материалы  и  документы  по  истории  музыки.  Т.  2  /  Под  ред.  М.В.  Иванова-Борецкого.  —  М.,  1934.  —  С.  55.

7.Сфера  //  Энциклопедический  словарь,  2009.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://dic.academic.ru/dic.nsf/es/89528/%D0%A1%D0%A4%D0%95%D0%A0%D0%90  (дата  обращения  4.04.2013).

8.Холопов  Ю.Н.  Изменяющееся  и  неизменное  в  эволюции  музыкального  мышления  //  Проблемы  традиции  и  новаторства  в  современной  музыке.  —  М.:  Сов.  композитор,  1982.  —  С.  52—104. 

9.Холопов  Ю.Н.  Очерки  современной  гармонии.  Исследование.  М.:  Музыка,  1974.  —  287  с.

10.Холопов  Ю.Н.  Современные  черты  гармонии  Прокофьева.  М.:  Музыка,  1967.  —  477  с. 

11.Эйлера  круги  //  Словарь  по  логике.  М.,  1997.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://dic.academic.ru/dic.nsf/logic/402  (дата  обращения  4.04.2013).

12.Weisstein,  Eric  W.  «Venn  Diagram».  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://mathworld.wolfram.com/VennDiagram.html  (дата  обращения  4.04.2013).