О  НАХОЖДЕНИИ  АСИМПТОТ  ГРАФИКОВ  ФУНКЦИЙ  В  ШКОЛЬНОМ  КУРСЕ  АЛГЕБРЫ  И  НАЧАЛ  АНАЛИЗА

Закирова  Нурия  Музиповна

канд.  техн.  наук,  доцент  Глазовского  государственного  педагогического  института,  г.  Глазов

Владыкина  Ирина  Владимировна

канд.  пед.  наук,  доцент  Глазовского  государственного  педагогического  института,  г.  Глазов

E-mail: 

ABOUT  FINDING  OF  ASYMPTOTES  OF  GRAPH  OF  FUNCTIONS  IN  SCHOOL  COURSE  OF  ALGEBRA  AND  BEGINNINGS  OF  ANALYSIS

Nuriya  Zakirova

candidate  of  technical  Sciences,  associate  Professor  of  Glazov  state  pedagogical  Institute,  Glazov

Irina  Vladykina

candidate  of  pedagogic  Sciences,  associate  Professor  of  Glazov  state  pedagogical  Institute,  Glazov

АННОТАЦИЯ

Курс  математического  анализа  любого  вуза  включает  изучение  темы  «Исследование  функций  и  построение  графиков».  С  данным  вопросом  учащиеся  знакомятся  уже  в  старших  классах  средней  школы.  Но  при  построении  графиков  функций  нахождение  асимптот  подробно  не  объясняется,  так  как  школьная  программа  по  математике  не  предусматривает  изучение  пределов.  В  данной  статье  предлагается  способ  нахождения  асимптот  графика  функции  без  использования  пределов. 

ABSTRACT

The  course  of  mathematical  analysis  of  any  institution  of  higher  learning  includes  the  study  of  theme  "Research  of  functions  and  construction  of  charts".  With  this  question  students  meet  already  in  the  senior  classes  of  high  school.  But  at  the  construction  of  charts  of  functions  being  of  asymptotes  in  detail  is  not  explained,  because  the  school  program  on  mathematics  does  not  envisage  the  study  of  limits.  In  this  article  the  method  of  being  of  asymptotes  of  chart  of  function  is  offered  without  the  use  of  limits.

Ключевые  слова:  функция;  график;  асимптота.

Keywords:  function;  graph;  asymptote. 

В  старших  классах  курса  «Алгебра  и  начала  анализа»  изучается  тема  «Исследование  функций  и  построение  графиков».  В  качестве  упражнений,  как  правило,  рассматриваются  целые  и  дробно-рациональные  функции.  На  графиках,  приводимых  в  качестве  примеров,  отмечены  вспомогательные  прямые,  к  которым  неограниченно  приближается  график  функции  при  удалении  её  переменной  точки  в  бесконечность.  Однако  не  всегда  авторы  учебников  разъясняют,  что  это  за  прямые  и  как  их  найти.  Например,  в  учебнике  Ш.А.  Алимова,  Ю.М.  Колягина,  Ю.В.  Сидорова  [2]  ничего  не  говорится  об  асимптотах,  тем  не  менее,  на  графике  функции    их  изображают  .  Аналогично  изложен  материал  и  в  учебнике  под  редакцией  А.Н.  Колмогорова  [1].  Не  упоминая  при  изложении  теории  об  асимптотах,  приводится  пример  ,  на  графике  которого  отмечены  прямые  .

В  учебниках  А.Г.  Мордковича  [7]  и  М.И.  Башмакова  [3]  чётко  введены  понятия  вертикальной  и  горизонтальной  асимптот  графика  функции.  О  наклонных  асимптотах  речи  нет.  Хотя  М.И.  Башмаков  при  исследовании  функции    отмечает,  что  «на  бесконечности»  дробь  ведёт  себя  примерно  также,  как  дробь 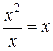 .  Авторы  Г.В.  Дорофеев,  Л.В.  Кузнецова,  Е.А.  Седова  в  курсе  алгебры  и  начал  анализа  [5]  с  помощью  опорных  точек  приходят  к  выводу,  что  при    график  функции    «уходит  в  +∞»  и  неограниченно  приближается  к  оси  ординат.  При    расстояние  между  графиком  и  прямой    стремится  к  нулю.

Во  всех  рассмотренных  учебниках  для  общеобразовательной  школы,  а  также  и  в  профильном  учебнике  (авторы  А.Г.  Мордкович,  П.В.  Семёнов)  [6]  вопрос  о  нахождении  наклонных  асимптот  не  рассматривается.

В  общеобразовательной  школе  строгое  определение  предела  функции  не  даётся,  пределы  не  вычисляются,  поэтому  вопрос  о  нахождении  асимптоты  с  помощью  предела  не  рассматривается.  Однако  при  исследовании  и  построении  графиков  дробно-рациональных  функций  в  школе  вопрос  о  существовании  асимптот  не  следует  опускать,  так  как  здесь  его  можно  решить  довольно  просто  (без  использования  предела).

Рассмотрим  несколько  правил,  которые  могут  быть  получены  из  общей  теории,  и  которых  следует  придерживаться  при  поиске  асимптот.  Если  знаменатель  дроби    (  —  многочлены)  в  точке    обращается  в  нуль,  а  числитель  ,  то  прямая    является  вертикальной  асимптотой  графика  функции.  Вертикальные  асимптоты  проходят  через  точки  разрыва  дробно-рациональной  функции.  Для  правильного  построения  графика  вблизи  вертикальных  асимптот  достаточно  выяснить,  каков  знак  функции  слева  и  справа  от  асимптоты.  Вертикальные  асимптоты  могут  быть  и  на  концах  области  определения,  например  .  Вертикальная  асимптота  .  Но  данная  функция  не  является  дробно-рациональной.

Чтобы  найти  горизонтальную  или  наклонную  асимптоты  нужно  числитель  рациональной  дроби  разделить  на  знаменатель,  то  есть  выделить  целую  часть  дроби.  Если  целая  часть  будет  числом,  равным  b,  то    является  горизонтальной  асимптотой  графика  функции 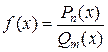 .  Если  же  целая  часть  равна  линейному  выражению  ,  то  прямая    будет  наклонной  асимптотой.  В  результате  имеем:

если  ,  степень  числителя  меньше  степени  знаменателя  (дробь  правильная),  то  график  имеет  горизонтальную  асимптоту  ;

если  ,  степень  числителя  равна  степени  знаменателя,  то    —  горизонтальная  асимптота  (b  —  это  отношение  коэффициентов  при  старших  степенях  х  многочленов  P_n(x)  и  Q_m(x));

если  ,  степень  числителя  на  единицу  больше  степени  знаменателя,  то  график  имеет  наклонную  асимптоту  ,  являющуюся  целой  частью  дробно-рациональной  функции.

В  работе  со  студентами  также  полезно  сформулировать  это  правило,  дополнительно  указав,  что  если  ,  то  вместо  прямолинейных  асимптот  появятся  криволинейные  асимптоты  в  виде  квадратичной,  кубической  парабол,  то  есть  графиков  типа    или  .  Этот  факт  согласуется  с  общей  теорией:  если  функцию    представить  в  виде  суммы  ,  причём    при  ,  то  график  функции    будет  неограниченно  приближаться  к  графику  функции  ,  т.е.  функция    будет  криволинейной  асимптотой  для  графика  .

Более  глубоко  данный  вопрос  можно  исследовать  с  учениками  во  внеурочное  время.  Здесь  интересен  опыт  факультативной  работы  учителя,  приведённый  в  журнале  «Математика  в  школе»  №  5  за  1999  год.  Ученики  вместе  с  учителем  экспериментально  проследили,  что  при    криволинейные  асимптоты  будут  гиперболами,  похожими  на  график  функции  .  Если  же  ,  то  криволинейные  асимптоты  похожи  на  график  функции  .  Полученные  на  факультативе  результаты  были  подтверждены  на  компьютере.

Наконец,  следует  заметить,  что  анализ  поведения  графика  функции  не  только  с  помощью  производных,  но  и  видением  наличия  асимптот  сразу,  с  первого  взгляда,  несомненно,  облегчает  построение  графика  в  целом.

Рассмотрим  примеры  функций  из  [4],  для  которых  можем  сразу  указать  прямолинейные  и  криволинейные  асимптоты.

1.  .

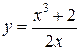Видим,  что  при    знаменатель  дроби  обращается  в  нуль,  а  числитель  нет.  Значит    −  вертикальная  асимптота.  Записав  функцию  в  виде 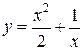   (выделив  целую  часть),  можем  сказать,  что  при    график  функции  будет  неограниченно  приближаться  к  графику 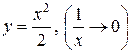 .  То  есть    будет  криволинейной  асимптотой.  Если  же  ,  то  ,  т.  к.  ,  а    (рис.  1).

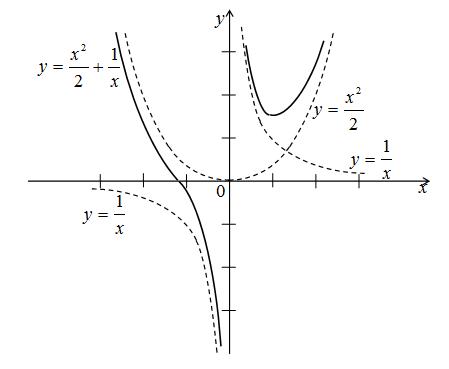
Рисунок  1.  График  функции 

2.  .

На  занятии  со  студентами,  используя  эквивалентность  бесконечно  больших  функций,  можем  записать 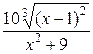 ~ 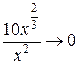 при  .  Значит,  график  функции  имеет  горизонтальную  асимптоту    (рис.  2).

Рисунок  2.  График  функции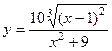

3.  .

При    имеем  неопределённость  .  Избавимся  от  неё,  умножив  числитель  и  знаменатель  данной  функции  на  сопряжённое  выражение.  Получим 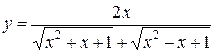 .  Данная  дробь  при    эквивалентна  выражению  .  При    имеем  ,    имеем    (рис.  3).

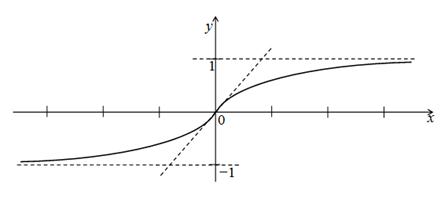
Рисунок  3.  График  функции

Приведенный  способ  нахождения  асимптот  графика  функции  будет  полезен  не  только  учащимся  средней  школы,  но  и  студентам  нематематических  специальностей,  у  которых  возникают  определенные  проблемы  при  изучении  пределов  в  вузовском  курсе  высшей  математики. 

Статья  подготовлена  в  рамках  работы  над  проектом  фундаментальных  исследований  №  6.5596.2011  «Педагогический  вуз  в  современном  образовательном  пространстве  России:  проблемы  и  перспективы».

Список  литературы:

1.Алгебра  и  начала  анализа.  10—11  кл.  [Текст]:  учеб.  для  10—11  кл.  общеобразоват.  учреждений  /  под  ред.  А.Н.  Колмогорова.  —  М.:  Просвещение,  2000.  —  365  с.

2.Алгебра  и  начала  анализа.  10—11  кл.  [Текст]:  учеб.  для  общеобразоват.  заведений  /  Ш.А.  Алимов,  Ю.М.  Колягин,  Ю.В.  Сидоров  и  др.  —  М.:  Просвещение,  2000.  —  384  с.

3.Башмаков  М.И.  Алгебра  и  начала  анализа.  10—11  кл.  [Текст]:  учеб.  для  общеобразоват.  учеб.  заведений.  /  М.И.  Башмаков.  —  М.:  Дрофа,  2000.  —  400  с.

4.Гюнтер  Н.М.  Сборник  задач  по  высшей  математике  [Текст]:  учеб.  пособие  /  Н.М.  Гюнтер,  Р.О.  Кузьмин.  —  СПб.:  Лань,  2003.  —  816  с.

5.Дорофеев  Г.В.  Алгебра  и  начала  анализа.  10  кл.:  Учеб.  для  образоват.  учреждений:  В  2  ч.  Ч.  1  [Текст]  /  Г.В.  Дорофеев,  Л.В.  Кузнецова,  Е.А.  Седова.  —  М.:  Дрофа,  2003.  —  320  с.

6.Мордкович  А.Г.  Алгебра  и  начала  математического  анализа.  10  класс.  В  2  ч.  Ч.  1.  Учебник  для  учащихся  общеобразовательных  учреждений  (профильный  уровень)  /  А.Г.  Мордкович,  П.В.  Семенов.  —  6-е  изд.,  стер.  —  М.:  Мнемозина,  2009.  —  424  с.

7.Мордкович  А.Г.  Алгебра  и  начала  анализа.  10—11  кл.  [Текст]:  в  2  ч.:  Учебник  для  общеобразоват.  учреждений  /  А.Г.  Мордкович.  —  М.:  Мнемозина,  2005.  —  375  с.