Статья опубликована в рамках: XLVII Международной научно-практической конференции «Личность, семья и общество: вопросы педагогики и психологии» (Россия, г. Новосибирск, 15 декабря 2014 г.)
Наука: Педагогика
Секция: Информационные технологии в образовании
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ИННОВАЦИОННЫЕ ТЕХНОЛОГИИ В ПРЕПОДАВАНИИ ГЕОМЕТРИИ
Андрафанова Наталия Владимировна
канд. пед. наук, доцент, Кубанский государственный университет, РФ, г. Краснодар
E -mail: nat_drofa@mail.ru
Закира Игорь Александрович
магистрант кафедры информационных образовательных технологий, Кубанский государственный университет, РФ, г. Краснодар
E -mail: nemec_26029209@mail.ru
Назарян Джулиета Сержиковна
преподаватель математики школы-лицея № 4, РФ, г. Краснодар
E -mail:
INNOVATIVE TECHNOLOGIES IN TEACHING GEOMETRY
Andraphanova Natalia
candidate of Pedagogics, Associate Professor, Kuban State University, Russia, Krasnodar
Zakira Igor
graduate student of the Informational Education Technologies Department, Kuban State University, Russia, Krasnodar
Nasaryan Dzhulietta
teacher of mathematics school-lyceum № 4, Russia, Krasnodar
АННОТАЦИЯ
В статье рассматривается применение современных компьютерных технологий в преподавании сложных вопросов геометрии на примере исследования свойств окружности девяти точек в интерактивной геометрической среде GeoGebra. Акцентируется внимание на таких возможностях интерактивной геометрической среды как наглядность, моделирование, динамика, использование которых привносит инновации в традиционную методику преподавания геометрии.
ABSTRACT
The article discusses of using modern computer technologies in teaching difficult geometry tasks by the example of the research of nine points circle quality in the dynamic geometry software GeoGebra. Attention is paid to the following opportunities of the interactive software as visualization, modeling, dynamics, the use of which brings innovations into traditional methods of teaching geometry.
Ключевые слова: интерактивная геометрическая среда; ИГС GeoGebra; информационно-коммуникационные технологии в геометрии.
Keywords : dynamic geometry software, software GeoGebra, information and communication technologies in geometry.
В условиях информатизации образования использование компьютерных технологий в преподавании геометрии является актуальным не только в связи с их стремительным развитием и проникновением в сферу образования, но и ввиду особенности предмета, в котором, по словам академика А.Д. Александрова, «строгая логика соединена с наглядным представлением, в котором они взаимно организуют и направляют друг друга» [2, с. 56].
Геометрия для школьников является одним из сложных предметов. Это подтверждает анализ результатов ЕГЭ по математике: выпускники школ либо не выполняют геометрические задачи вообще, либо решают только плоскостные задачи, и лишь незначительная часть на экзамене приступает к решению стереометрических задач, хотя и не многие получают положительный результат.
Причиной подобной ситуации, как считает Г.Д. Глейзер, является сложившаяся традиционная методика преподавания геометрии: «школьный учебник и сложившаяся у нас традиция преподавания привели к представлению о том, что основная цель обучения геометрии — развитие логического мышления у школьников…» [7, с. 69]. Такая методика используется в ущерб образным компонентам мышления. Поэтому в последнее время многие исследователи обращают внимание на поиск путей совершенствования обучения геометрии, основанного на оптимальном сочетании логического и наглядно-образного мышления.
Использование современных информационно-коммуникационных технологий (ИКТ) позволяет изменить традиционные подходы к изучению многих вопросов геометрии. При этом применение ИКТ как средства обучения не должно сводиться к простой иллюстрации устного изложения учебного материала, а должны быть задействованы все его возможности: наглядность, моделирование, динамика.
Принцип наглядности
Великий математик К. Гаусс утверждал, что математика не столько для ушей, сколько для глаз. Принцип наглядности обучения в современной дидактике — это ориентация на использование в процессе обучения разнообразных средств наглядного представления соответствующей учебной информации.
Американский психолог Р. Арнхейм даже ввел термин «визуальное мышление», означающий «мышление посредством визуальных (зрительных) операций», а его работы положили начало современным исследованиям роли образных явлений в познавательной деятельности.
Применение компьютера как современного технического средства обработки и представления информации позволяет использовать его широкие возможности для создания наглядных образов. Если в традиционном обучении под наглядностью понимают, прежде всего, иллюстративный компонент, обеспечивающий передачу информации от учителя к ученику посредством зрительных образов и форм, то в условиях компьютерного обучения наглядность реализуется посредством предъявления информации об объектах и процессах в компьютерной форме в статике и в динамике. «Поставщиком» наглядности выступает уже не учитель, а компьютер [3, с. 78]. Такая методика подачи учебного материала позволяет исправить ситуацию, когда за математической формулировкой (теоремой, определением) у учащегося отсутствует конкретное представление образа объекта, неправильно воспринимаются его существенные признаки, установленные этим утверждением.
Академик А.Д.Александров в статье «О геометрии» отмечал, что геометрическому образованию изначально присущ этакий «треугольник»: логика-воображение-практика, и если выкинуть из него хотя бы одну вершину, то получим искаженный курс геометрии. При этом наиболее значимая вершина в этом «треугольнике» — воображение. Педагогическая практика показывает, что визуализация геометрических знаний с помощью компьютерных технологий развивает у школьников видение геометрических объектов и их свойств.
Принцип моделирования
В современной дидактике утверждается, что принцип наглядности — это систематическая опора не только на конкретные визуальные предметы и их изображения, но и на их модели. Роль учебных моделей (как вида иллюстраций) в формировании теоретических понятий убедительно раскрыта В.В. Давыдовым. Он характеризует учебные модели как своеобразный сплав наглядности и понятия, конкретного и абстрактного, и предлагает рассматривать моделирование как дидактический принцип, дополняющий наглядность. Соотношение этих принципов В.В. Давыдов определяет следующим образом: «…там, где содержанием обучения выступают внешние свойства вещей, принцип изобразительной наглядности себя оправдывает. Но там, где содержанием обучения становятся связи и отношения предметов, — там наглядность далеко не достаточна. Здесь вступает в силу принцип моделирования» [8, с. 59].
Компьютерное моделирование, связанное с визуализацией геометрических моделей, является полезным инструментом в геометрических исследованиях, с помощью которого можно экспериментально обнаруживать новые интересные геометрические факты. Результаты компьютерного эксперимента убеждают учащихся в истинности утверждения больше, чем представленные в учебнике логические доказательства. У.Е. Минтоном было отмечено, что существенные признаки и связи, зафиксированные в модели, становятся наглядными для учащихся тогда, когда эти признаки, связи были выделены самими детьми в их собственном действии, т. е. когда они сами участвовали в создании модели.
Компьютерный эксперимент позволяет
· определить характеристики объекта в соответствии с заданными условиями;
· выявить свойства объекта при определенных дополнительных условиях;
· подтвердить или опровергнуть гипотезу исследования [5, с. 23].
Принцип динамики
Компьютерная динамическая интерпретация геометрических понятий является инновационным подходом в обучении геометрии. Динамическая иллюстрация — это реализация компьютерными средствами эффекта движения иллюстративного объекта. Принцип динамики положен в основу систем динамической геометрии или интерактивных геометрических сред.
Динамические модели — интерактивные модели, свойства которых пользователь может целенаправленно изменять в процессе их использования (эксперимента, наблюдения, исследования). Для современного школьника интерактивная геометрическая среда не только новая инновационная технология изучения геометрического материала, но и привычная, естественная технология обработки графической информации.
Один из основателей компьютерной графики Айвен Сазерленд однажды отметил уникальные особенности компьютера как средства визуализации графической информации: «Дисплей, подключенный к ЭВМ, представляется мне окном в Алисину Страну чудес, где программист может изображать любые объекты, описываемые хорошо известными законами природы, либо чисто воображаемые объекты, подчиняющиеся законам, записанным в программе. С помощью дисплеев я сажал самолет на палубу движущегося авианосца, следил за движением элементарной частицы в потенциальной яме, летал в ракете с околосветовой скоростью и наблюдал за таинствами внутренней жизни вычислительной машины» [1].
В 1961 году А.Сазерленд создал первый интерактивный графический пакет “Sketchpad” («Альбом»). Эта программа позволяла рисовать простые фигуры на дисплее, сохранять их, а также использовать готовые прототипы фигур. Программа позволяла моделировать объекты: можно было работать с изображением автомобиля, изменяя размеры его шин, но, не затрагивая остальную часть модели.
В настоящее время интерактивные графические пакеты, позволяющие выполнять геометрические построения с помощью геометрических объектов, задавая соотношения между ними, весьма разнообразны. Их можно разделить на два вида: программы двухмерной геометрии (2D) и программы трехмерной геометрии (3D).
Свойство интерактивности геометрической среды позволяет:
· выполнять построение чертежа для вводимых пользователем исходных данных;
· изменять параметры объектов при сохранении общего алгоритма построения чертежа;
· получать сведения о свойствах изображенных фигур;
· проводить компьютерный эксперимент с целью сбора данных о свойствах изучаемого объекта или наблюдения за характером изменения его свойств [4, с. 59].
Для изучения геометрического материала можно использовать программу трехмерной геометрии GeoGebra. Она разработана Маркусом Хохенвартером, бесплатно распространяемая, обладает простым интерфейсом пользователя, имеет русскоязычную версию. Вокруг этой программы в последние годы сформировалось международное сообщество исследователей и преподавателей из разных стран мира, принимающих участие в конференциях по вопросам продвижения интерактивной геометрической среды (ИГС). Специальный выпуск Европейского журнала современного образования (European Journal of Contemporary Education) № 4 2013 был посвящён использованию GeoGebra в учебном процессе [10]. Покажем применение возможностей ИГС GeoGebra для построения динамического чертежа окружности девяти точек.
Окружность девяти точек — это окружность, проходящая через середины сторон произвольного треугольника, основания его высот и середины отрезков, соединяющих вершины с точкой пересечения высот треугольника (рисунок 1).
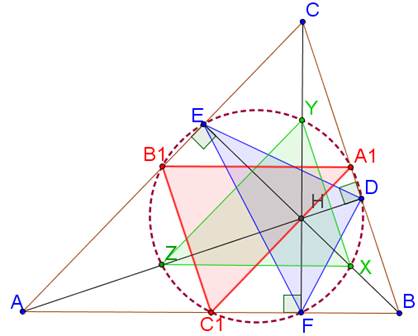
Рисунок 1. Окружность девяти точек
Европейские авторы часто называют эту окружность «окружностью Эйлера» [9, с. 33]. В 1765 году Л. Эйлер доказал, что ортотреугольник, вершинами которого являются основания высот треугольника, и серединный треугольник, вершины которого — середины сторон треугольника, имеют общую описанную окружность, отсюда еще одно название окружности — «окружность 6 точек». Некоторые математики называют эту окружность «окружностью Фейербаха», так как К. Фейербахом в 1821 году было опубликовано первое полное доказательство общего результата.
Связанные с этой окружностью задачи являются одними из красивейших задач геометрии. Некоторые из них представлены в учебнике 10—11 класса Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др. [6, с. 200]. Возможности GeoGebra позволяют не только достаточно быстро построить окружность девяти точек, используя готовые инструменты среды, но и продемонстрировать в динамике ее свойства.
Окружность девяти точек : основания трех высот произвольного треугольника, середины трех его сторон и середины трех отрезков, соединяющих его вершины с ортоцентром (точкой пересечения высот), лежат на одной окружности, радиус которой в два раза меньше радиуса описанной окружности.
Алгоритм построения окружности девяти точек в среде GeoGebra включает в себя следующие шаги построения:
Таблица 1.
|
Шаги построения |
Используемые инструменты |
|
Построить произвольный треугольник ABC |
|
|
Отметить середины сторон треугольника: A1, B1, C1 |
|
|
Построить высоты треугольника: AD, BE, CF (точки D, E, F определяются как точки пересечения двух объектов) |
|
|
Отметить точку пересечения высот H как пересечение двух объектов |
|
|
Отметить середины отрезков AH, BH, CH, соединяющих вершины треугольника с точкой пересечения высот, как Z, X, Y |
|
|
Построить окружность по трем точкам |
|
Построенная таким образом окружность описана около трех треугольников (рисунок 1):
· ![]() , соединяющего середины сторон исходного треугольника (серединный треугольник);
, соединяющего середины сторон исходного треугольника (серединный треугольник);
· ![]() , соединяющего основания высот исходного треугольника (ортотреугольник);
, соединяющего основания высот исходного треугольника (ортотреугольник);
· ![]() , вершинами которого являются середины отрезков, соединяющих вершины исходного треугольника с ортоцентром.
, вершинами которого являются середины отрезков, соединяющих вершины исходного треугольника с ортоцентром.
Прямая Эйлера : ортоцентр, центроид (точка пересечения медиан треугольника) и центр описанной окружности произвольного треугольника лежат на одной прямой. Центроид делит расстояние от ортоцентра до центра описанной окружности в отношении 2 : 1.
Прямая, на которой лежат эти три точки, называется прямой Эйлера этого треугольника (рисунок 2). Алгоритм построения, наглядно подтверждающий данный факт, включает в себя следующие шаги:
Таблица 1.
|
Шаги построения |
Используемые инструменты |
|
Построить произвольный треугольник ABC |
|
|
Построить медианы треугольника: найти середины сторон треугольника, соединить середины сторон с вершинами треугольника - AА1, BB1, CC1 |
|
|
Отметить точку пересечения медиан М (центроид) как пересечение двух объектов |
|
|
Построить высоты треугольника AD, BE, CF (точки D, E, F определяются как точки пересечения двух объектов) |
|
|
Отметить точку пересечения высот H (ортоцентр) как пересечение двух объектов |
|
|
Построить серединные перпендикуляры к сторонам треугольника |
|
|
Отметить точку пересечения серединных перпендикуляров О как пересечение двух объектов |
|
|
Провести прямую линию через две точки, например, О и H |
|
Используя инструмент Перемещать для вершины С треугольника ABC, можно, изменяя вид треугольника, наглядно и понятно показать истинность утверждения для произвольного треугольника или же создать динамический чертеж рассмотренного геометрического построения.
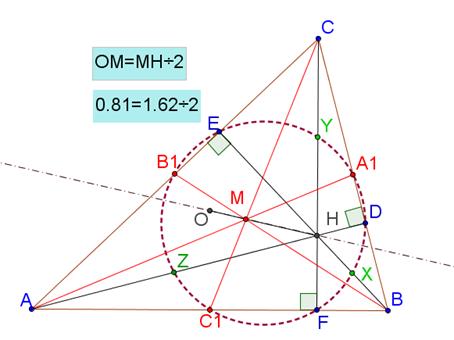
Рисунок 2. Прямая Эйлера
Свойства прямой Эйлера и окружности девяти точек :
1. Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности, а ее радиус в два раза меньше радиуса описанной окружности (рисунок 3).
2. Точки, симметричные точке пересечения высот H (или их продолжений) относительно сторон треугольника и их середин, лежат на описанной окружности.
3. Точки, симметричные центру описанной окружности относительно прямых, содержащих средние линии треугольника, лежат на окружности девяти точек.
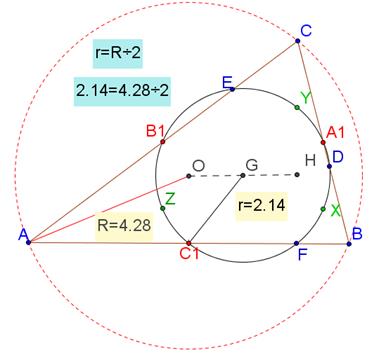
Рисунок 3. Демонстрация первого свойства
Перечисленные свойства прямой Эйлера и окружности девяти точек можно предложить учащимся «открыть» экспериментально, выполняя практические задания. Приведем пример одного из таких заданий.
1. Постройте произвольный треугольник ABC.
2. Постройте высоты AA1, BB1, CC1 треугольника. Точку пересечения высот обозначьте H.
3. Опишите окружность вокруг треугольника АВС.
4. Постройте точку А2, симметричную точке H относительно прямой, содержащей сторону BC.
5. Постройте точку В2, симметричную точке H относительно прямой, содержащей сторону АC.
6. Постройте точку С2, симметричную точке H относительно прямой, содержащей сторону АB.
7. Сформулируйте свойство расположения точек, симметричных относительно сторон треугольника.
В результате выполнения практического задания учащимися происходит экспериментальное самостоятельное «открытие» свойств.
Таким образом, использование широких возможностей интерактивной геометрической среды позволяет изменить традиционные подходы к изучению многих сложных вопросов геометрии, как было показано на примере задачи Эйлера. По сравнению с традиционными наглядными средствами ИГС как инновационная технология изучения геометрического материала предоставляет качественно новые дидактические возможности.
Список литературы
1.Абинов А.Г. Человек или машина? Серия «Знак вопроса», 1989 № 2. М., издательство «Знание». [Электронный ресурс] — Режим доступа. — URL: http://znak.traumlibrary.net/book/zv8902/zv8902.html#work002001003 (дата обращения: 01.12.2014).
2.Александров А.Д. «О геометрии» // Журнал «Математика в школе», — 1980. — № 3, — с. 56—62.
3.Андрафанова Н.В., Назарян Д.С. Интерактивная геометрическая среда как средство компьютерной наглядности в обучении геометрии. Материалы международной научно-практической конференции «Информационные технологии в обеспечении федеральных государственных образовательных стандартов», Елец, 2014, — с. 76—80.
4.Андрафанова Н.В., Назарян Д.С. Интерактивная геометрическая среда как средство развития познавательного интереса школьников. Проблемы и перспективы развития образования в России, 2014. — № 27, — с. 59—65.
5.Андрафанова Н.В., Закира И.А. Поддержка исследовательской деятельности школьников средствами ИГС. Проблемы и перспективы развития образования в России, 2014. — № 30, — с. 21—26.
6.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10—11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни. М.: Просвещение, 2009.
7.Глейзер Г.Д. Каким быть школьному курсу геометрии // Математика в школе, — 1990. — № 7. — с. 68—71.
8.Давыдов В.В. Виды обобщения в обучении М.: Просвещение, 1972.
9.Коксетер Г.С.М, Грейтцер С.Л. Новые встречи с геометрией. Выпуск 14 серия «Библиотека математического кружка». М. Наука, 1978.
10.European Journal of Contemporary Education. — 2013. — № 4 [Электронный ресурс] — Режим доступа. — URL: http://ejournal1.com/ru/ (дата обращения: 01.12.2014).
дипломов


Оставить комментарий