Статья опубликована в рамках: L-LI Международной научно-практической конференции «Личность, семья и общество: вопросы педагогики и психологии» (Россия, г. Новосибирск, 13 апреля 2015 г.)
Наука: Педагогика
Секция: Педагогическая психология
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ПРОРЫВНЫЕ ТЕХНОЛОГИИ ФОРМИРОВАНИЯ АВТОНОМНОСТИ ЛИЧНОСТИ ОБУЧАЮЩИХСЯ НА УРОКАХ МАТЕМАТИКИ: ВНЕДРЕНИЕ МЕЖПРЕДМЕТНОЙ ИНТЕГРАЦИИ В УСЛОВИЯХ ПРОФИЛИЗАЦИИ СТАРШЕЙ ШКОЛЫ
Нешумаев Михаил Викторович
ассистент кафедры математики Амурского гуманитарно-педагогического государственного университета, учитель математики МОУ СОШ № 18, РФ, г. Комсомольск- на-Амуре
INDIVIDUALS STUDIED AT MATH LESSONS: IMPLEMENTATION OF INTERSUBJECT INTEGRATION UNDER CONDITIONS OF HIGH SCHOOL PROFILISATION
Mikhail Neshumaev
assistant of Math Chair, Amur State University of Humanities and Pedagogy, Teacher of Math, Municipal Educational Institution Secondary General School № 18, Russia, Komsomolsk on Amur
АННОТАЦИЯ
В рамках реализации ФГОС общего образования приоритетным для учителя становится воспитание самостоятельности личности обучающихся, формирование у них «способности учиться». Однако, именно формирование в личности такого свойства, как «автономность», по мнению автора, становится фундаментальной базой для воспитания её самостоятельности и креативности. В статье представлен экспериментальный опыт по внедрению и реализации инновационного подхода при формировании автономности личности обучающихся на уроках математики в условиях профилизации старшей школы.
ABSTRACT
As part of Federal State Educational Standard of general education, the development of pupils’ individual autonomy and forming their "ability to learn" become a priority for the teacher. However, the formation of such properties as "autonomy", according to the author, is the fundamental basis for the education of pupils’ independence and creativity. The article deals with experimental experience to establish and implement innovative approach in the formation of pupils’ personal autonomy at math lessons in terms of profilisation of high school.
Ключевые слова: автономность личности обучающихся; межпредметная интеграция, ФГОС общего образования.
Keywords: pupils’ individual autonomy; intersubject integration; Federal State Educational Standard of general education.
1. Описание психолого-педагогического эксперимента по формированию автономности личности обучающихся в разных методических условиях преподавания математики
Перед началом проведения эксперимента мы скомплектовали в начале учебного 2013—2014 года два 10 класса в разных общеобразовательных школах. Учителя математики, участвующие в формирующем эксперименте с данными классами, обладали автономностью, имеют одинаковый возраст, прошли одинаковую профессиональную подготовку в АмГПГУ, но реализующие разные методические подходы в обучении учеников:
1. 10 «М» класс (экспериментальный) — профильный медицинский класс, который был сформирован 1.09.2013 года. Учитель внедрял нетрадиционный подход в обучении и воспитании школьников
2. 10 «Б» класс (контрольный) — обычный непрофильный класс, который был сформирован 1.09.2003 года. Учительница внедряла традиционный подход в обучении и воспитании школьников
Обоснование и описание условий формирующего эксперимента
Методика математического образования на основе интеграции алгебры, геометрии, биологии, химии, физики и медицины в экспериментальном профильном медицинском классе общеобразовательной школы
Реализация межпредметных связей не может происходить сама по себе; для этого нужна специальная организация учебного материала и самого процесса обучения, направленная на установление этих связей. Учителю следует, прежде всего, отбирать материал, который представляет межпредметные связи, выбирать формы обучения, для того, чтобы межпредметные контакты стали достоянием сознания учащихся, следует включать материал о них в учебно-познавательную деятельность.
Поскольку в интегрированном обучении рассматриваются разнообразные междисциплинарные проблемы, расширяющие рамки действующих программ и учебников для общеобразовательных школ, то необходимо подчеркнуть, что при таком подходе сочетаются разнообразные методы обучения: лекция и беседа, объяснение и управление самостоятельной работой учащихся, наблюдение и опыт, сравнение, анализ и синтез. Перед учителями математики, работающими в профильных медицинских классах, стоит важная задача — построить процесс обучения таким образом, чтобы в нем предельно полно интегрировались знания по математике и предметам естественнонаучного цикла: биологии, химии и, непосредственно, самой медицины.
Рассмотрим более подробно каждое из перечисленных направлений интеграции, реализуемых нами в преподавании. Для решения многих задач по химии требуется умение решать пропорции, умение сокращать дроби и грамотно вести расчёты, а также округлять числа. Большое познавательное значение имеет построение графиков, отражающих, например, зависимости: процентной концентрации раствора от массы растворённого вещества в данной массе раствора, теплового эффекта реакции от массы образовавшегося вещества, степени диссоциации вещества от концентрации его раствора. Опора на математические методы позволяет количественно оценивать закономерности химических процессов, логически обосновывать отдельные законы и теории.
В школьном курсе математики существует достаточно много тем, которые способствуют осознанному пониманию и биологических понятий, а также известных биологических законов. Например, «Золотое сечение» можно легко интерпретировать через призму гармонии различных форм природы. «Теория вероятностей и математическая статистика» может быть учителем отражена в генетике популяций, законе Харди-Вайнберга, а «Геометрическую прогрессию» можно изучить на примере возможностей размножения организмов. При изучении темы «Осевая и центральная симметрии» вопрос о наличии их видов в природе способствует формированию целостного представления о симметрии. В ходе беседы нужно выявить причины появления разных типов симметрии у животных в процессе развития животного мира и причины симметрии у растений. На наш взгляд, учащийся, выбравший для себя медицинский профиль, в процессе обучения должен осознать, что современные математика и биология определенно свидетельствуют о том, что сложное похоже на случайное. В самом деле, живое на любом уровне организации жизни (клеточном, организационном, популяционном и т. п.) представлено даже не сложными, а сверхсложными системами, охарактеризовать которые просто невозможно без математических приемов, формул и методов. Занимаясь биологическими экспериментами и наблюдениями, исследователь всегда имеет дело с количественными вариациями частоты встречаемости или степени проявления различных признаков или свойств. Поэтому без специального математического аппарата, а именно, статистического анализа, обычно нельзя решить, каковы возможные пределы случайных колебаний изучаемой величины.
Безусловно, медицина, биология и химия, не являются исключением в процессе интеграции математики со смежными дисциплинами. Многие современные врачи считают, что дальнейший прогресс медицины находится в прямой зависимости именно от математических успехов в ней и диагностике, в частности степени их взаимосвязи и взаимной адаптации. Подходя к лечению больных, врач должен быстро и профессионально поставить диагноз, выбрать правильный лекарственный препарат, методику лечения и максимально их индивидуализировать. Сегодня очень важно увидеть новую патологию человека, и среди наиболее перспективных технологий, используемых для этих целей, по праву, является математика. Развитие её вычислительных методов, нарастание мощности электронной техники позволяют в наши дни выполнять точные расчеты в области динамики сложнейших живых и неживых систем с целью прогнозирования их проведения. При организации обучения математике посредством приобщения к медицине предлагаем изучение тем «Объёмы тел», «Длина. Единицы измерения» на примере вычисления антропометрических индексов. В акушерстве, гинекологии и фармакологии находят своё отражение «Проценты» и «Пропорции». Например, педиатрия поможет учителю математики визуализировать «Арифметическую прогрессию». Более того, учащиеся способны освоить приёмы вычисления средней арифметической величины варьирующего признака построения вариационного ряда и вариационной кривой оперативного вмешательства в хирургии, которые обоснованы теорией вероятностей: нормальным и показательным распределениями случайной величины, критерием Стьюдента.
Преподавание математики в медицинских классах посредством интегрированных уроков тесно сопряжено с организацией исследовательской деятельности учащихся. Такой вид работы видится нам позволяющим формировать автономную, самостоятельную, активную позицию учащихся в учении, развивать общеучебные умения и компетенции. В основе исследовательской деятельности лежит идея практической или теоретической значимости той или иной проблемы. Стоит отметить, что интеграция предметов математики и естествознания позволяет также выявлять одаренных и творческих учащихся. Для получения видимого результата проделанной работы им требуются базовое образование по многим дисциплинам. Это и есть показатель использования учащимися комплекса знаний по математики, биологии, химии и медицины.
В качестве примера приведем перспективный план изучения предмета «Алгебра и начала анализа» в 10 «М» (медицинском) классе на 2013—2014 учебный год (см. табл. 1). Теоретическую и методическую подготовку к данному математическому учебному курсу составили источники, приведённые нами в списке литературы [1; 2; 3; 4; 5; 6; 7].
Таблица 1.
Перспективный план изучения предмета «Алгебра и начала анализа» в 10 классе по учебнику Ю.М. Колягина «Алгебра и начала анализа для 10 класса: базовый и профильный уровни»
|
Изучаемая глава |
Дата проведения |
Тема занятия |
Межпредметные связи урока |
Итоговое занятие |
|
Алгебра 7—9 классов (повторение) |
06.09.2013 г. |
Линейная и квадратичная функции |
Медицина, биология |
Урок-зачёт |
|
20.09.2013 г. |
Прогрессии и сложные проценты |
Химия, биология, медицина |
||
|
04.10.2013 г. |
Начала статистики |
|||
|
18.10.2013 г. |
Логика |
Биология, медицина |
||
|
Делимость чисел |
01.11.2013 г. |
Сравнения |
Биология |
Урок-форум |
|
15.11.2013 г. |
Решение уравнений в целых числах |
Медицина, биология, химия |
||
|
Многочлены. Алгебраические уравнения |
29.11.2013 г. |
Схема Горнера |
Биология |
Урок-зачёт |
|
06.12.2013 г. |
Бином Ньютона |
Медицина, биология |
||
|
Степень с действительным показателем |
13.12.2013 г. |
Бесконечно убывающая геометрическая прогрессия |
Медицина, биология, физика |
Урок-диспут |
|
20.12.2013 г. |
Степень с рациональным и действительным показателями |
|||
|
Степенная функция |
27.12.2013 г. |
Степенная функция, её свойства и график |
Биология, медицина, химия |
Урок-консилиум |
|
10.01.2014 г. |
Иррациональные уравнения |
Медицина, физика |
||
|
Показательная функция |
17.01.2014 г. |
Показательная функция, ее свойства и график |
Медицина, биология, химия, физика |
Урок-зачёт |
|
24.01.2014 г. |
Показательные уравнения |
|||
|
31.01.2014 г. |
Показательные неравенства |
Приведем пример одного из итоговых зачетных уроков для учащихся 10-го профильного медицинского класса, на котором реализуется интеграция знаний по математике с биологией, химией, физикой и медициной.
Тема урока: «Решение показательных уравнений и неравенств»
Тип урока: интегрированный урок.
Вид урока : урок-зачёт (групповая и индивидуальная работа).
Время проведения : сдвоенный открытый урок (внедрение 04.02.2014 г., МОУ СОШ № 18 г. Комсомольска-на-Амуре, Хабаровского края, учитель: Нешумаев М.В.)
Цель: развить и закрепить познавательный интерес на основе межпредметных связей, сформировать положительную мотивацию, самостоятельность и автономность личности учащихся.
Образовательные задачи : обобщить имеющиеся у учащихся знания о решении показательных уравнений и неравенств как стандартного, так и повышенного уровней, формировать умение выбирать рациональный метод при решении уравнений и неравенств, встречающихся в ЕГЭ; посредством анализа исследовательских работ акцентировать внимание учащихся на возможности интеграции знаний из курсов математики, биологии, химии и медицины; продолжить формировать умения работать с дополнительной литературой.
Развивающие задачи : развивать у учащихся умения излагать мысли, выделять главное, оценивать, делать выводы; способствовать развитию познавательного интереса, логического мышления; формировать коммуникативные умения сверстников.
Воспитательные задачи : формировать научное мировоззрение, целостную картину мира; воспитывать настойчивость, умение преодолевать трудности при выполнении работы.
Оборудование: индивидуальный пакет учащегося, включающий в себя листы для проверки формул, для самостоятельной работы, карточки с набором заданий для выполнения дифференцированной домашней работы; биологические муляжи «сердце», «глазное яблоко», «матка» и «череп»; презентация; классная доска.
Межпредметные связи урока : биология, химия, физика, медицина
План урока: 1) организационный момент (вступительное слово учителя, настрой учащихся на урок); 2) актуализация опорных знаний (работа с индивидуальными листами для проверки формул по свойствам степеней; работа учащихся на центральной части доски и «за доской»; взаимопроверка); 3) доклады творческих групп о проделанной ими исследовательской работе: группа «гинекологи»; группа «кардиологи»; группа «офтальмологи»; группа «патологоанатомы».
Выполнение индивидуальной самостоятельной работы (выполнение математических заданий в течение урока с опорой на решения уравнений докладчиков у доски);
«Бонусная карта урока» (на протяжении урока учащиеся, успевающие выполнить свою самостоятельную работу, могут попробовать себя в состязании с компьютером, предлагающим решение показательных уравнений и неравенств повышенного уровня сложности из ЕГЭ);
Итог урока (заключительное слово учителя; освещение заданий для выполнения дифференцированной домашней работы; рефлексия учащихся).
Рассмотренный выше план урока представляет собой зачётное занятие по теме «Решение показательных уравнений и неравенств». Ученикам предлагаются нестандартные условия: учебный класс разделён на четыре зоны, каждая из которых определяет принадлежность учащегося к соответствующей творческой группе («гинекологи», «кардиологи», «офтальмологи», «патологоанатомы»). В течение урока учащиеся имеют возможность принять участие в различных видах деятельности: постановка и анализ целей урока, работа у доски, взаимопроверка и оценивание ответа другого ученика, выполнение самостоятельной работы, защита проектов, индивидуальная работа за компьютером.
В контексте данного урока особо стоит подчеркнуть способ выбора докладчика от каждой группы. Руководителю группы предоставляется право тянуть жребий, и отвечает тот, чьё имя оказалось на листке бумаги. Такой способ видится нам честным и необычным, исключающим любое неравенство в группе и заставляющим всех быть одинаково включёнными в процесс подготовки.
Во время защиты исследовательских работ учителю необходимо акцентировать внимание на выявленной учащимися взаимосвязи математики, биологии, химии и медицины. По ходу занятия ориентировать их на нюансы решений уравнений и неравенств, которые могут пригодиться на ЕГЭ. В течение урока происходит многократная смена деятельности, следствием которой становится выполнение большого объёма заданий при малом утомлении. В начале занятия каждому учащемуся выдается индивидуальный пакет, включающий в себя листы для проверки формул, для самостоятельной работы, карточки с набором заданий для выполнения дифференцированной домашней работы. Выполнение индивидуальной самостоятельной работы предусматривается на протяжении всего урока. Ученики выполняют работу, при необходимости обращаясь к решению, предложенному докладчиком у доски. Кроме всего, в течение занятия учащиеся, успевающие выполнять свою самостоятельную работу, могут попробовать себя в состязании с компьютером, предлагающим решение показательных уравнений и неравенств повышенного уровня сложности из ЕГЭ по математике.
Логичным завершением урока станет ориентирование, призыв к перенесению опыта, полученного на занятии, опыта глубокой и сплочённой работы, взаимодействия таких, разобщённых, на первый взгляд, направлений как математика, биология, медицина и химия, в их дальнейшую жизнь и профессиональную деятельность врача. Приведем примеры реализации интегративного подхода в математическом образовании школьников 10-го медицинского класса в их исследовательской работе (интеграция математики и медицины). Ниже представлены примеры решения некоторых задач, рассматриваемых творческими группами на уроках.
Задача № 1 (предложена группой гинекологов на зачёте по теме «Сложные проценты»): Акушерам-гинекологам известно, что в норме физиологическая потеря при родах составляет 0,5 % от массы тела. Определите кровопотерю, если масса женщины 63 кг? Ответ укажите в (мл).
Решение: воспользуемся формулой процентных соотношений:
![]()
Ответ: при родах кровопотеря составила 0,315 мл.
Задача №2 (диспут по теме «Степень с действительным показателем»): Найдите площадь поверхности тела человека, имеющего рост 170 см и вес 70 кг.
Решение: для определения площади поверхности тела воспользуемся формулой Д.Ф. Дьюбоса: ![]() , где
, где ![]() — рост человека (см),
— рост человека (см), ![]() — вес человека (кг),
— вес человека (кг), ![]() — постоянные Гелхана-Джорджа.
— постоянные Гелхана-Джорджа.
![]() — искомая площадь поверхности тела
— искомая площадь поверхности тела
Ответ: ![]()
Задача № 3 (задание группе «кардиологов» на уроке-зачёте по теме «Решение показательных уравнений и неравенств»): Необходимо определить время вакуумирования в кардиологической барокамере при проведении хирургической операции, используя пятишаговый насос, откачиваемый за шаг 25 ![]() газа, при необходимости откачки в 600
газа, при необходимости откачки в 600 ![]() газа. Рассчитано, что при этом наблюдается падение давления со 100 атм. до 96 атм.
газа. Рассчитано, что при этом наблюдается падение давления со 100 атм. до 96 атм.
Решение: при создании вакуума конечное давление в определённой ёмкости связано с начальным давлением следующей формулой:
![]()
Ответ: ![]() ч.
ч.
2. Сравнительный анализ результатов формирующего эксперимента на основе сформированности автономности личности учеников, а также их уровня учебной мотивации, психологического климата класса и сплоченности школьного коллектива
Рассмотрим подробнее результаты итогового тестирования испытуемых школьников после внедрения интегрированной методики обучения (алгебры, геометрии, биологии, химии, физики и медицины).
Таблица 2.
Результаты сформированности автономности личности школьников после формирующего эксперимента
|
Испытуемые |
«Автономные» |
«Зависимые» |
«Неопределенные» |
|
Экспериментальная группа |
52,6 % |
26,3 % |
21,1 % |
|
Контрольная группа |
15,8 % |
31,6 % |
52,6 % |
|
Сравнение % по критерию Фишера (φ кр. = 2,31) |
φ эмп. = 2,485 |
φ эмп. = 0,358 |
φ эмп. = 2,065 |
Из таблицы 2 видно, что в экспериментальном классе доминирует количество учеников с «автономностью» личности (φ эмп. = 2,485), в группе «зависимых» различий не обнаружено, однако в группе «неопределенных» обнаружена тенденция перехода учеников экспериментальной группы в категорию «автономных» учеников (φ эмп. = 2,065), то есть они пока «неавтономные», но по прошествии какого-то времени станут таковыми с высокой долей вероятности.
Обследование школьников по методике «Невербальный семантический дифференциал» позволила описать личностный портрет учителей, внедряющих разные методики обучения математики, рассмотрим полученные характеристики учителей в отражении школьников, по таблице 3.
Таблица 3.
Сравнительный анализ психологического портрета учителей экспериментальной и контрольной групп, обладающих автономностью
|
Учитель экспериментальной группы, внедривший интегрированный подход |
Учительница контрольной группы, внедрившая традиционный подход |
|
Учитель, по мнению учащихся, более привлекательный как личность, они симпатизируют ему, он является для них эталоном поведения, примером для подражания. Для него характерны такие качества как уверенность в себе, независимость. Выражена экстравертированность, с реакциями внешнеориентированными на ситуацию. Учитель имеет привычную для ребят устойчивую структуру личности. Вовлечен в социальные процессы, активно участвует в общении с окружающими его детьми. |
Учитель как личность менее привлекает учащихся. Для него характерны такие качества как уверенность в себе, независимость. Пользуется слабым авторитетом среди ребят, тем самым шансы стать для них примером для подражания заметно снижены. Реакции, внешнеориентированы на ситуацию. Учитель имеет наиболее хаотичную по отношению к социальной норме структуру личности. Он незначительно вовлечен в социальные процессы, что находит своё отражение в более заметной дистанции по отношению к общению с ребятами. |
Рассмотрим и сравним психологический климат 10-х классов по тесту «Учебный климат». В таблице 4 приведены показатели учебного климата экспериментального и контрольного классов. Полученные результаты говорят о высоком уровне преподавания в экспериментальном 10 «М» классе, о сформированном школьном коллективе за полугодие, так как этот класс был сформирован недавно — 1 сентября 2013 года, контрольный 10 «Б» класс сформирован давно, школьный коллектив существует на протяжении 10 лет (сформирован 1 сентября 2003 года). Мы можем утверждать, что это полная заслуга учителей, работающих в этом 10 «М» классе и внедренной методики обучения математики. Критерий Фишера не обнаружил различий в психологическом климате классов, он одинаково хорош.
Таблица 4.
Соотношение показателей психологического климата в 10-х классах
|
Класс |
Уровень психологического климата |
Показатель критерия Фишера |
|
10 «М» |
38,9 |
φ эмп. = 1,120 |
|
10 «Б» |
33,1 |
Изучение уровней развития учебной мотивации школьников показало довольно высокие результаты в обеих группах. В таблице 5 представлено процентное соотношение уровней общей учебной мотивации.
Таблица 5.
Соотношение уровней общей учебной мотивации в 10-х классах
|
Уровни |
Экспериментальная группа (n = 19) |
Контрольная группа (n = 19) |
|
Низкий |
— |
— |
|
Средний |
89,48 % |
78,95 % |
|
Высокий |
10,52 % |
21,05 % |
Далее, на рисунке 1, представлена диаграмма, которая показывает в сравнении развитие видов учебных мотивов школьников, которые в совокупности образуют учебную мотивацию класса:
1. Познавательные мотивы
2. Коммуникативные мотивы
3. Эмоциональные мотивы
4. Мотивы саморазвития
5. Позиция школьника
6. Мотивы достижения успеха
7. Мотивы одобрения (поощрения, наказания)
8. Профессионально-жизненное самоопределение
Максимальное количество баллов по тесту — 100.
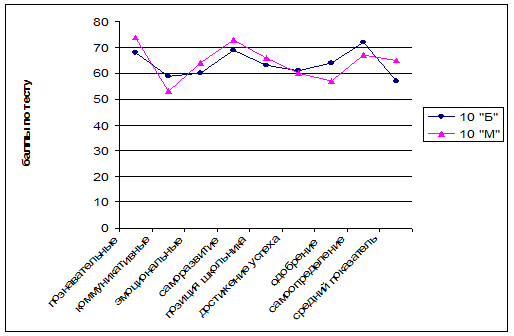
Рисунок 1. Динамика учебной мотивации по видам учебных мотивов в 10-х классах
Полученные нами результаты пилотажного формирующего психолого-педагогического эксперимента, который длился с сентября 2013 г. по февраль 2014 г., позволяют заключить, что интеграция естественно-научного блока дисциплин решает комплекс учебных задач. Кроме того, позволяет школьникам расширять границы собственного самосознания, что способствует развитию их индивидуальной познавательной активности и формированию автономности личности, которую мы считаем ключевым образованием личности взрослого человека, её самостоятельности и креативности.
Список литературы:
1.Батуев А.С. Биология: Большой справочник для школьников и поступающих в вузы / А.С. Батуев, М.А. Гуленкова, А.Г. Еленевский и др. 3-е изд., стереотип. М.: Дрофа, 2000. — 668 с.: ил. — (Большие справочники для школьников и поступающих в вузы).
2.Габриелян О.С. Химия. 11 класс: учеб. для общеобразоват. учреждений / О.С. Габриелян, Г.Г. Лысова. 6-е изд., стереотип. М.: Дрофа, 2006. — 362 с.
3.Габриелян О.С. Химия. 10 класс. Базовый уровень: учеб. для общеобразоват. учреждений / О.С. Габриелян. 3-е изд., перераб. М.: Дрофа, 2007. — 191 с.
4.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов втузов. 3-е изд., перераб. и доп. М.: Высш. школа, 1979. — 400 с.
5.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для студентов вузов. 5-е изд., перераб. и доп. М.: Высш. школа, 1977. — 479 с.
6.Колягин Ю.М. Алгебра и начала анализа: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни / Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин; под ред. А.Б. Жижченко. М.: Просвещение, 2008. — 368 с.
7.Кулагин П.Г., Межпредметные связи в процессе обучения, М., 1981.
8.Максимова В.Н., Груздева Н.В. Межпредметные связи в обучении. М.: Просвещение, 1987. — 187 с.
9.Максимова В.Н. Межпредметные связи в процессе обучения. М.: Просвещение, 1998. — 191 с.
10.Сергеева Т.Ф. Актуальные проблемы школьного математического образования / Т.Ф. Сергеева // Математика и математическое образование: материалы международной конференции «Proceedings of the Forty First Spring Conference of the Union of Bulgarian Mathematicians Borovetz», April 9–12, 2012. — С. 107—112.
11.Федорова В.Н. Межпредметные связи естеств.-матем. дисциплин, под ред. В.Н. Федоровой, М., 1980. — 352 с.
дипломов


Оставить комментарий