Статья опубликована в рамках: I Международной научно-практической конференции «Личность, семья и общество: вопросы педагогики и психологии» (Россия, г. Новосибирск, 15 февраля 2010 г.)
Наука: Педагогика
Скачать книгу(-и): Сборник статей конференции часть I, Сборник статей конференции часть II, Сборник статей конференции часть III
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
МЕТОДИЧЕСКАЯ РАБОТА УЧИТЕЛЯ МАТЕМАТИКИ ПО ВЫЯВЛЕНИЮ И ПРЕДУПРЕЖДЕНИЮ АССОЦИИРОВАННЫХ ОШИБОК ШКОЛЬНИКОВ
Самсонов П.И.
канд. пед. наук, учитель математики, г. Москва
E-mail: zirta@mail.ru
Процесс обучения любому школьному предмету всегда сопровождается появлением у учеников ошибок: одни из них связаны с обычной торопливостью и невнимательностью, другие получены в результате непрочно усвоенного алгоритма применения правила или закона. В арсенале современного учителя существует очень много приемов и способов осуществления работы по их предупреждению и исправлению. Причем эта работа может быть не только статичной, но и вполне творческой, когда выявленная ошибка помогает свести полученный результат к запоминающемуся ученикам абсурду и тем самым способствует лучшему усвоению изучаемых понятий или алгоритму действий, развивает необходимые навыки самоконтроля.
Важным в этой деятельности является то, что появление указанных ошибок происходит в момент изучения темы и поддается коррекции в процессе работы над ней. Однако, существует особый вид ошибок, коварство которых заключено как раз в том, что их появление не просто отсрочено по времени, а бывает что и на достаточно длительные временные промежутки. Это, ошибки, полученные в результате неверных ассоциаций, неверного переноса алгоритма действия на объекты, которые между собой похожи, но к которым он не применим, так называемые ассоциированные ошибки.
Рассмотрим пример.
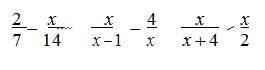
Первое уравнение встречается школьнику в 5 классе и относится к задаче – "решить пропорцию". Опираясь на основное свойство пропорции, ученик запишет 2×14=7×х, откуда будет следовать, что х=4, и ответ: 4. С целью лучшего запоминания метода решения этого уравнения им иногда предлагают словесную "подсказку" – в таких равенствах нужно просто перемножить "крест на крест".
Придя в 8 класс и встретившись со следующим уравнением, он получает подкрепление этому правилу "перемножение крест на крест", а на уроке химии, при выполнении подсчетов по уравнению химической реакции, это же правило закрепляется на уровне навыка.
Все было бы хорошо: ученики уверенно решают такой тип уравнений, могут применить свои знания и на уроках химии, и на уроке физики, и даже при работе с темой масштаб на уроке географии. Но в тот момент, когда в 10–11классах им предстоит решать уже неравенство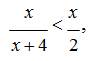 
то можно получить его Следствие которое во–первых исходному неравенству 
неравносильно, а потому ошибочно, а во–вторых получено в результате ассоциированного переноса алгоритма действия с уравнениями на неравенство, к которым уже не применимо.
Закрепленная ассоциация является настолько сильной, что даже то, что ученики изучали свойства числовых неравенств и знают, что при умножении обеих частей неравенства на отрицательное число необходимо изменить знак неравенства на противоположный, а о знаке значений выражения х, которое принимает как положительные значения, так и отрицательные, ничего не известно, их не остановило. Ассоциация по виду похожему на уравнение оказалась сильнее, она быстрее активизируется, чем хорошо известные правила действий с неравенствами.
Возможность по эффективному предупреждению появления таких ошибок заключается в формировании другой ассоциации, которая будет индуцироваться раньше и тормозить возникновение ошибочной. Самый простой подход – сугубо методический. Поскольку основным алгоритмом решения неравенств является метод интервалов, связанный с определением промежутков знакопостоянства, то необходимо сформировать ассоциацию, что у неравенства "справа должен быть ноль".
Применительно к приведенному неравенству это будет выглядеть так:.
Дальнейшее решение уже не выведет учащихся на возникновение ассоциированной ошибки.
Примером другого типа образования ассоциированной ошибки, является транслирование алгоритма решения неполных квадратных уравнений на
неравенство
х2 < 4 . Весьма часто можно встретить такие решения:
х2 < 4; x < ±2 ,
которые появляются в результате непродуманных действий учителя по формированию навыков решения неполных квадратных уравнений. Причем, заметим, что, в данном случае, научив решать неполные квадратные уравнения, учителю по прошествии некоторого времени придется немало потрудиться, чтобы нивелировать возникшие проблемы с решением неравенств.
Здесь можно поступить так же, как и в предыдущем случае. Однако, наиболее ценным может оказаться предупреждение такой ассоциированной ошибки за счет изменения самой методики обучения решению неполных квадратных уравнений, вообще исключающая обращение к символу ±. В этом случае у учащихся не будет образца, который индуцирует образование такой ассоциации.
Приведем пример такого решения:
х2 = 3; х2 - 3 = 0; (х -3)(х +3) = 0;
х = 3
или
х = - 3.
Важно заметить, что это не решение частно–методической задачи по предупреждению отдельного вида ошибок в решениях задач у учащихся. Такой подход позволяет широко применять навыки, полученные в результате его освоения.
Например, использовать их в задаче по преобразованию выражения.
b2 - 7
+
7 = (b -7 )(b +7 ) +
7 = b - 7 +
7 = b.
b + 7
b + 7
Построение правильной цепочки действий в решении задачи, которая позволяет учителю, зная о характерных ошибках учащихся старших классов, предупреждать их за счет изменений в методике преподавания в более младших классах – это еще один из методических приемов работе учителя по предупреждению ассоциированных ошибок учащихся.
Методика предупреждения появления ассоциированных ошибок в работах учащихся основана на том, что:
– в обучении исключается образец действия или записи, могущий привести к их образованию;
– формируется опережающая ассоциация, тормозящая проявление неверной.
Особенность ассоциированных ошибок, заключающаяся в том, что их проявление отсрочено по времени указывает на необходимость знать такие ошибки. Это в первую очередь достигается кропотливым анализом различных диагностических работ, которые выполняют учащиеся, но не с точки зрения коллекционирования ошибок, совершенных учениками, а с точки зрения составления так называемой карты ошибок.
При таком подходе можно, например, увидеть, что при решении иррациональных уравнений, ученики очень часто не проверяют отрицательные по значению корни уравнения–следствия, а сразу записывают их в посторонние, мотивируя это тем "что в корнях отрицательных чисел не бывает". Следовательно, что бы избежать путаницы у учеников между отрицательным числом и отрицательным значением выражения, а значит предупредить появление ассоциированной ошибки, для первых уроков по теме "решение иррациональных уравнений" необходимо предлагать уравнения, в которых у уравнения–следствия будет два отрицательных корня, один из которых окажется посторонним для исходного уравнения.
Умение предупреждать ошибки, а не корректировать их, можно по праву отнести к высшему мастерству в работе современного учителя.
дипломов
Оставить комментарий