ПОЛИЭДРАЛЬНЫЙ  ГРАФ  ЗАДАЧИ  ОБ  ОСТОВНОМ  ДЕРЕВЕ  ОГРАНИЧЕННОЙ  СТЕПЕНИ

Бондаренко  Владимир  Александрович

д-р.  физ.-мат.  наук,  профессор,  зав.  кафедрой  дискретного  анализа, 

ЯрГУ  им.  П.Г.  Демидова, 
РФ,  г.  Ярославль

E -mail:  bond@bond.edu.yar.ru

Николаев  Андрей  Валерьевич

канд.  физ.-мат.  наук,  доцент 
ЯрГУ  им.  П.Г.  Демидова, 
РФ,  г.  Ярославль

E -mail:  werdan.nik@gmail.com

Шовгенов  Джамболет  Азаматович

аспирант 
ЯрГУ  им.  П.Г.  Демидова, 
РФ,  г.  Ярославль

E-mail: 

1-SKELETON  OF  THE  DEGREE  CONSTRAINED  MINIMUM  SPANNING  TREE  PROBLEM

Vladimir  Bondarenko

doctor  of  Science,  Professor,  Head  of  Discrete  Analysis  Department,

P.G.  Demidov  Yaroslavl  State  University, 
Russia,  Yaroslavl

Andrei  Nikolaev

candidate  of  Science,  Associate  Professor,

P.G.  Demidov  Yaroslavl  State  University, 
Russia,  Yaroslavl

Dzhambolet  Shovgenov

graduate  Student, 

P.G.  Demidov  Yaroslavl  State  University, 
Russia,  Yaroslavl

Работа  выполнена  при  частичной  финансовой  поддержке  гранта  РФФИ  №  14-01-00333  и  гранта  Президента  Российской  Федерации  МК-5400.2015.1.

АННОТАЦИЯ

Исследуются  комбинаторно-геометрические  характеристики  задачи  о  минимальном  остовном  дереве  ограниченной  степени.  Устанавливается  сверхполиномиальный  рост  кликового  числа  и  NP-полнота  проверки  смежности  вершин  полиэдрального  графа  задачи.

ABSTRACT

We  study  combinatorial  and  geometric  properties  of  the  degree  constrained  minimum  spanning  tree  problem.  We  establish  a  superpolynomial  lower  bound  on  the  clique  number  and  the  NP-completeness  of  the  vertex  adjacency  testing  for  the  1-skeleton  of  the  problem  polytope. 

Ключевые  слова:  остовное  дерево;  полиэдральный  граф;  кликовое  число;  NP-полная  задача;  гамильтонова  цепь.

Keywords:  spanning  tree;  1-skeleton  of  a  polytope;  clique  number;  NP-complete  problem;  hamiltonian  chain.

Значительное  число  работ,  связанных  с  вычислительной  сложностью  комбинаторных  задач,  направлено  на  изучение  геометрических  объектов,  ассоциированных  с  задачами.  Чаще  всего  такими  объектами  являются  многогранники  задач  и  графы  этих  многогранников.  В  частности,  кликовое  число  (размер  наибольшего  полного  подграфа)  полиэдрального  графа  задачи  служит  нижней  оценкой  вычислительной  сложности  в  широком  классе  алгоритмов,  основанных  на  линейных  сравнениях.  Более  того,  выяснилось,  что  эта  характеристика  полиномиальна  для  известных  полиномиально  разрешимых  задач  и  сверхполиномиальна  для  труднорешаемых  (см.,  например,  [2;  3]).

Рассмотрим  две  задачи  следующего  вида:  задан  реберно-взвешенный  граф    и  некоторое  множество  T  его  подграфов,  требуется  найти  подграф  из  T,  имеющий  минимальный  суммарный  вес.

Минимальное  остовное  дерево  (minimum  spanning  tree,  MST).  Требуется  найти  в  связном  графе  G  остовное  дерево  с  минимальным  весом.

Задача  об  остовном  дереве  полиномиально  разрешима,  например,  алгоритмами  Прима  и  Краскала.

Минимальное  остовное  дерево  ограниченной  степени  (degree  constrained  minimum  spanning  tree,  DCST).  В  этой  задаче  требуется  найти  дерево  минимального  веса  среди  всех  остовных  деревьев,  степени  вершин  которых  не  превосходят  заданную  величину  k.

Задача  об  остовном  дереве  ограниченной  степени  является  NP-полной  [4].

Обозначим  через  n  —  число  вершин  графа  G,  а  через  d  —  количество  ребер  в  полном  графе  на  n  вершинах  ().  Рассмотрим  пространство  R^d,  координаты  точек  в  котором  ассоциированы  с  ребрами  графа  G.  Каждому  элементу  t  из  T  сопоставим  его  характеристический  вектор  ,  положив  равными  единице  значения  тех  координат,  которые  соответствуют  ребрам,  принадлежащим  t,  а  остальные  координаты  приняв  равными  нулю.  Совокупность  характеристических  векторов  обозначим  через  X.  Тогда  выпуклая  оболочка  множества  X  называется  многогранником  задачи.  Полиэдральным  графом  задачи  называется  граф  многогранника,  множеством  вершин  которого  служит  множество  геометрических  вершин  (в  данном  случае  это  X),  а  множеством  ребер  —  совокупность  геометрических  ребер,  то  есть  множество  одномерных  граней.

Полиэдральный  граф  многогранника  MST_n  задачи  об  остовном  дереве  для  графа  G  на  n  вершинах  полностью  описан,  точное  значение  кликового  числа  приведено  в  работе  [1].

Утверждение  1.   Кликовое  число  полиэдрального  графа  многогранника  MST_n  полиномиально  по  n  и  равно 

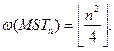
Рассмотрим  многогранник  DCST_n,k  задачи  о  минимальном  остовном  дереве  ограниченной  степени  в  графе  на  n  вершинах.  Для    и    обозначим  через

и  построим  дерево  t  специального  вида.  Разобьем  множество  вершин  на  s  подмножеств  вида    по    вершине  в  каждом.  Все  оставшиеся  вершины,  которых  будет  от  2  до  ,  разобьем  на  два  подмножества    и  .  Рассмотрим  конструкцию  следующего  вида:  в  каждом  подмножестве  V_i  все  вершины  соединяются  ребрами  с  только  с  вершиной  v_i  (Рис.  1).  Отметим,  что  степени  вершин  v₀  и  v_s+1  по  построению  не  могут  превосходить  k.

Лемма  1.   Граф  t_h,  получаемый  из  дерева  t  отбрасыванием  вершин  v₀,  v_s+1  и  v_i,j  вместе  с  ребрами  (v_i,j,v_i),  является  гамильтоновой  цепью  с  концевыми  вершинами  v₁  и  v_s.

Доказательство.  По  построению  степени  вершин  v₁  и  v_s  не  могут  быть  меньше  ,  а  степени  вершин  {v₂,…,v_s–1}  меньше  .  Так  как  степени  вершин  в  дереве  t  не  превосходят  k,  то  граф,  получаемый  после  отбрасывания  вершин,  может  быть  только  гамильтоновой  цепью,  соединяющей  v₁  и  v_s.

Рисунок  1.  Конструкция  остовного  дерева  ограниченной  степени

Рассмотрим  совокупность  T_k  всех  остовных  деревьев  описанного  вида.  По  лемме  1  каждое  такое  дерево  содержит  цепь  t_h  с  концевыми  вершинами  v₁  и  v_s,  проходящую  через  вершины  {v₂,…,v_s–1}.  Верно  и  обратное:  каждой  цепи  указанного  вида  соответствует  дерево  из  T_k.  Обозначим  через  HC_1s  выпуклую  оболочку  характеристических  векторов  гамильтоновых  цепей  между  вершинами  v₁  и  v_s.

Лемма  2.   Вершины  x  и  y  многогранника  DCST_n,k,  отвечающие  деревьям  из  T_k,  несмежны  тогда  и  только  тогда,  когда  несмежны  соответствующие  им  вершины  x_h  и  y_h  многогранника  HC_1s.

Доказательство.  Предположим,  что  вершины  x_h  и  y_h  многогранника  HC_1s  несмежны.  Тогда  некоторая  их  выпуклая  комбинация  совпадает  с  выпуклой  комбинацией  остальных  вершин  многогранника  HC_1s.

Каждой  гамильтоновой  цепи  из  HC_1s  однозначно  соответствует  остовное  дерево  из  T_k.  Дополним  равенство  координатами,  соответствующими  отброшенным  ребрам  и  получим  равенство

означающее,  что  вершины  x  и  y  многогранника  DCST_n,k  несмежны.

Пусть  теперь  вершины  x  и  y  несмежны,  тогда

У  точек  x  и  y  все  координаты,  соответствующие  ребрам  (v_i,j,v_i),  совпадают,  так  как  эти  ребра  фиксированы  для  остовных  деревьев  из  T_k,  а  значит  они  совпадают  и  у  точек  z,  что  позволяет  перейти  к  равенству

Каждому  остовному  дереву  из  T_k  однозначно  соответствует  гамильтонова  цепь  между  вершинами  v₁  и  v_s  из  HC_1s.  Таким  образом,

и  вершины  x_h  и  y_h  многогранника  HC_1s  несмежны.

Лемма  2  дает  возможность  воспользоваться  свойствами  задачи  коммивояжера  для  изучения  многогранника  DCST_n,k.  Для  этого  достаточно  учесть  следующий  простой  факт:  две  вершины  многогранника  HC_1s  гамильтоновых  цепей  смежны  тогда  и  только  тогда,  когда  в  многограннике  задачи  коммивояжера  смежны  вершины,  соответствующие  гамильтоновым  циклам,  образованным  при  отождествлении  крайних  вершин  в  одну.  Таким  образом  из  леммы  2  и  известного  результата  Х.  Пападимитриу  [5]  следует

Теорема  1.   Задача  распознавания  смежности  вершин  многогранника  DCST_n,k  является  NP-полной.

Теорема  2.   Кликовое  число  полиэдрального  графа  многогранника  DCST_n,k  задачи  об  остовном  дереве  ограниченной  степени  сверхполиномиально  по  s:

Для  доказательства  теоремы  2  достаточно  воспользоваться  леммой  2  и  нижней  оценкой  кликового  числа  полиэдрального  графа  многогранника  TSP_n  задачи  коммивояжера  для  n  городов  [1]: 

Таким  образом,  классическая  задача  о  минимальном  остовном  дереве  и  задача  о  дереве  ограниченной  степени  имеют  принципиально  отличные  полиэдральные  характеристики.  Для  классической  задачи  известны  полиномиальные  алгоритмы,  полностью  описан  полиэдральный  граф  задачи,  и  установлено,  что  его  кликовое  число  полиномиально  по  размерности  пространства.  При  этом  задача  об  остовном  дереве  ограниченной  степени  является  труднорешаемой,  полиэдральный  граф  задачи  являются  крайне  сложными:  даже  проверка  смежности  вершин  является  NP-полной  задачей,  кликовое  число  графа  сверхполиномиально  по  размерности  пространства. 

Список  литературы:

1.Белов  Ю.А.  О  плотности  графа  матроида  //  Модели  исследования  операций  в  вычислительных  системах.  Яросл.  гос.  ун-т.,  Ярославль.  1985.  —  C.  95—100.

2.Бондаренко  В.А.,  Максименко  А.Н.  Геометрические  конструкции  и  сложность  в  комбинаторной  оптимизации.  М.:  ЛКИ,  2008.  —  184  с.

3.Бондаренко  В.А.,  Николаев  А.В.  Комбинаторно-геометрические  свойства  задачи  о  разрезе  //  Доклады  Академии  наук.  —  Т.  452,  —  №  2.  —  2013.  —  С.  127—129.

4.Гэри  M.,  Джонсон  Д.  Вычислительные  машины  и  труднорешаемые  задачи.  М.:  Мир.  1982.  —  416  с.

5.Papadimitriou  C.H.  The  Adjacency  Relation  on  the  Traveling  Salesman  Polytope  is  NP-Complete  //  Mathematical  Programming.  —  Vol.  14,  —  Iss.  1.  —  1978.  —  P.  312—324.