ТРАЕКТОРИИ,  ОБЛАДАЮЩИЕ  ВЫСОКОЙ  ПАРАМЕТРИЧЕСКОЙ  ЧУВСТВИТЕЛЬНОСТЬЮ,  ВОЗНИКАЮШИЕ  В  ОДНОМ  КЛАССЕ  СИНГУЛЯРНО  ВОЗМУЩЁННЫХ  СИСТЕМ

Островский  Илья  Борисович

ассистент  кафедры  «Высшая  математика» 
Алтайского  государственного  технического  университета, 
РФ,  г.  Барнаул

Е-mail: 

TRAJECTORIES  POSSESSING  HIGH  PARAMETRIC  SENSIBILITY  ARISING  IN  THE  CLASS  OF  SINGULAR  PERTURBED  SYSTEMS

Ilya  Ostrovskiy

p ost-graduate  student  of  “Higher  Mathematics”  Chair, 
Altay  State  Technical  University, 
Russia,  Barnaul

АННОТАЦИЯ

Исследуются  пучки  траекторий,  обладающих  высокой  параметрической  чуствительностью,  так  называемых  траекторий-уток,  возникающие  в  одном  классе  сингулярно  возмущенных  систем  с  одной  медленной  и  одной  быстрой  переменными  и  малым  параметром  ε.  В  качестве  приближения  пучка  траекторий-уток  на  участке  их  движения  вдоль  медленной  кривой,  предлагается  кривая,  заданная  параметрически,  дающая  оценку  отклонения  пучка  от  медленной  кривой  и  приближающая  его  с  порядком  .

ABSTRACT

Beams  of  trajectories  possessing  high  parametric  sensitivity,  so-called  duck  trajectories,  arising  in  one  class  of  singularly  perturbed  systems  with  one  slow  and  one  fast  variable  and  a  small  parameter  ε  are  under  study.  As  an  approximation  of  the  beam  duck  trajectories  in  the  area  of  their  movement  along  the  slow  curve,  the  curve  is  offered  prescribed  parametrically,  giving  an  assessment  of  the  slow  beam  deflection  curve  and  bringing  it  to  the  order. 

Ключевые  слова:   сингулярные  возмущения;  медленная  кривая;  траектории-утки.

Keywords:   singular  perturbance;  slow  variable;  duck  trajectory. 

В  настоящей  работе  рассматривается  класс  сингулярно  возмущенных  систем  обыкновенных  дифференциальных  уравнений  вида

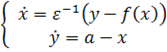    (1)

Здесь  x  ∈  R,  y∈R,  ε>0  ∈R-  малый  параметр,  f  ∈  ,  a  ∈  R  —  дополнительный  параметр.

Причем  еще  предполагается,  что  функция  f  всюду  выпукла  книзу,  т.  е.    при  всех  ,  и  имеет  единственную  точку  минимума    ,  T.  е  ,  <0  при  x  <    ,  >0  при  x>. 

Система  (1)  задает  так  называемое  быстро-медленное  векторное  поле  с  одной  быстрой  переменной  x  и  одной  медленной  переменной  y.  Практически  во  всех  точках  фазовой  плоскости  (x,y)  . 

Множество  точек  на  фазовой  плоскости  (x,y),  в  которых  скорость  быстрой  переменной  обращается  в  нуль,  т.  е.  ,  называется  медленной  кривой.  В  нашем  случае  медленная  кривая  есть  график  функции  y=f(x).  Участок  графика,  где  f(x)  возрастает,  является  притягивающим  (т.е.  локально  в  окрестности  этого  участка  быстрое  движение  направлено  к  нему),  а  участок  графика,  где  f(x)  убывает,  является  отталкивающим  (т.  е.  в  окрестности  этого  участка  быстрое  движение  направлено  от  него). 

Для  системы  (1)  известны  следующие  интересные  результаты  (см.  [1]  и  [3]). 

При  малых  ε  существует  интервал  ()  порядка    ,  расположенный  в  окрестности  порядка  O(ε)  точки  минимума  ,  такой,  что  когда  a∈()  система  (1)  имеет  целые  пучки  так  называемых  траекторий-уток  —  траекторий,  проходящих  вначале  длительное  (порядка  единицы)  расстояние  вдоль  притягивающей  ветви  медленной  кривой,  а  затем  длительное  (порядка  единицы)  расстояние  вдоль  отталкивающей  ветви  медленной  кривой.  Причем  для  любого  отрезка  [],  содержащего  точку  минимума    существует  соответствующее  значение  ∈(),  такое,  что  при  a=  система  (1)  имеет  пучок  траекторий-уток,  проходящих  вдоль  медленной  кривой  на  отрезке  [].  Все  траектории-утки  экспоненциально  близки  между  собой  на  участке  движения  вдоль  медленной  кривой.  Т.  е.,  если  у  нас  есть  две  траектории-утки,  соответствующие  одному  и  тому  же  или  разным  значениям  a∈(),  то  на  участке,  где  обе  траектории  движутся  вдоль  медленной  кривой,  расстояние  между  ними  есть  величина  порядка    . 

Проблема  численного  нахождения  траекторий-уток  при  малых  ε  заключается  в  том,  что  область  значений  параметра  a,  отвечающих  уткам,  является  невероятно  узкой:  если  предположить,  например,  что  ε  имеет  порядок  ,  то,  чтобы  «поймать»  утку,  требуется  проводить  вычисления  с  точностью,  приближенно  оцениваемой  числом  ,  т.  е.  учитывать  более  40  000  знаков  после  запятой.  Поэтому  при  малых  значениях  ε  для  траекторий-уток  приходится  довольствоваться  приближенными  вычислениями. 

В  настоящей  работе  в  качестве  приближения  пучка  траекторий-уток,  движущихся  вдоль  медленной  кривой  на  отрезке  [],  содержащем  точку  минимума    (этот  отрезок  может  иметь  сколь  угодно  большую  длину),  предлагается  кривая,  заданная  параметрически,  дающая  оценку  отклонения  пучка  от  медленной  кривой  (на  фазовой  плоскости(x,y)  пучок  траекторий-уток  проходит  выше  данной  кривой)  и  приближающая  его  при  ε→  0  с  порядком  O(). 

Далее  мы  не  будем  сразу  же  предъявлять  нашу  кривую.  Вместо  этого  мы  приведем  ряд  рассуждений,  последовательно  приводящий  нас  к  ее  построению.

Сразу  скажем,  что,  так  как  мы  изучаем  траектории-утки  системы  (1)  при  малых  ε,  то  предполагается,  что  параметр    (если  быть  точнее,  то  величина∣-  ∣  есть  величина  порядка  ε). 

Далее  заметим,  что  изоклины  системы  (1)  находятся  в  явном  аналитическом  виде.

Изоклина  горизонтальных  наклонов    есть  вертикальная  прямая  x=a.

Изоклина  вертикальных  наклонов    есть  кривая  y=f(x),  т.  е.  медленная  кривая.

Изоклина,  соответствующая  конечному  ненулевому  наклону  k,  находится  из  соотношения:    и  есть  кривая  .  Она  также  как  и  медленная  кривая  всюду  выпукла  книзу    и  имеет  единственную  точку  минимума,  ,  которая  находится,  как  корень  уравнения  .  Варьируя  k  в  пределах  -<  k<,  мы  получим  однопараметрическое  семейство  изоклин,  задаваемое  (за  исключением  случая  ,когда  k=0)  уравнением:  y(x,)=. 

Заметим,  что  т.  к.  ,  то  в  той  части  фазовой  плоскости,  где  ,  изоклина,  соответствующая  меньшему  наклону    будет  располагаться  выше  изоклины,  соответствующей  большему  наклону  ,  а  в  той  части,  где  ,  наоборот,  изоклина,  соответствующая  меньшему  наклону    будет  располагаться  ниже  изоклины,  соответствующей  большему  наклону  .  Заметим  также,  что  абсцисса,  точки  касания  изоклины,  соответствующей  наклону  ,  с  векторным  полем,  ε(),  находится,  как  корень  уравнения  .  В  общем  случае  он  может  быть  найден  численно  с  заданной  точностью. 

Далее  сформулируем  и  докажем  следующую  лемму:

Лемма  1.   При  малых  значениях  ε,  множество  точек  касания  с  векторным  полем  изоклин,  соответствующих  отрицательным  наклонам    будет  располагаться  в  области  ,  а  множество  точек  касания  с  векторным  полем  изоклин,  соответствующих  положительным  наклонам  : 

,  будет  располагаться  в  области 

  .

Доказательство.   Продифференцировав  обе  части  равенства  ,  получим:    (2).  Тогда  в  силу  того,  что  при  всех  ,  на  интервале 

  ,  функция    ведет  себя  следующим  образом:  она  возрастает,  когда  ,  убывает,  когда    и  имеет  точку  максимума  при  . 

На  интервале  ,    убывает,  когда  ,  возрастает,  когда    имеет  точку  минимума  при  . 

Таким  образом,  среди  точек  из  множества    наибольшее  значение  абсциссы  будет  иметь  точка  ,  а  среди  точек  из  множества    наименьшее  значение  абсциссы  будет  иметь  точка  .

Т.  к.  ,  а  ,  то  по  теореме  Лагранжа  имеем:

  ,  где    .  Т.  к  функция  >0  и  непрерывна  на  отрезке

  ,  то  по  теореме  Вейерштрасса,  существуют  числа    и  ,  такие,  что

  на  отрезке  .  Тогда  имеем:

.  Следовательно,  при  малых  ε  величина    есть  величина  порядка  ,  а  т.  к.,  как  уже  говорилось  выше,  величина  ∣-  ∣  есть  величина  порядка  ε,  то  при  малых  ε  точка  будет  располагаться  в  области  ,  а  значит  и  все  точки  из  множества    будут  располагаться  в  области  .  Абсолютно  аналогично  показывается,  что  величина    есть  величина  порядка  ,  а  значит  при  малых  ε,  точка    будет  располагаться  в  области  ,  а  значит,  и  все  точки  из  множества    будут  располагаться  в  области  .  Лемма  доказана. 

Рассмотрим  теперь,  касательную  к  изоклине  ,  соответствующей  отрицательному  наклону  ,  проведенную  в  точке  (  ε(),    касания  изоклины  с  векторным  полем. 

Ее  уравнение  имеет  вид:  .  (3)

В  силу  выпуклости  книзу  изоклины  ,  касательная  =0  при    будет  располагаться  ниже  изоклины  .  Тогда  в  силу  того,  что  в  области    изоклины,  соотвествующие  меньшим  наклоном  располагаются  выше  изоклин,  соответствующих  большим  наклонам,  любой  отрезок  прямой  =0,  лежащий  в  области  ,  и  не  содержащий  точки  ,  будет  отрезком  без  контакта  с  траекториями  системы(1)  и  в  точках  этого  отрезка  будет  выполняться  неравенство:  .  Отметим,  также,  что  любой  отрезок  прямой  =0,  лежащий  в  области  ,  будет  также  отрезком  без  контакта  с  траекториями  системы  (1)  и  в  точках  этого  отрезка  будет  также  выполняться  неравенство:  .

Рассмотрим  теперь,  касательную  к  изоклине  ,  соответствующей  положительному  наклону  ,  проведенную  в  точке  (  ε(),    касания  изоклины  с  векторным  полем. 

Ее  уравнение  имеет  вид,  аналогичный  уравнению  (3): 

.  (4)

В  силу  выпуклости  ,  касательная  =0  при    будет  располагаться  ниже  изоклины  .  Тогда  в  силу  того,  что  в  области    изоклины,  соотвествующие  меньшим  наклоном  располагаются  ниже  изоклин,  соответствующих  большим  наклонам,  любой  отрезок  прямой  =0,  лежащий  в  области  ,  и  не  содержащий  точки  ,  будет  отрезком  без  контакта  с  траекториями  системы(1)  и  в  точках  этого  отрезка  будет  выполняться  неравенство:  .  Отметим,  также,  что  любой  отрезок  прямой  =0,  лежащий  в  области  ,  будет  также  отрезком  без  контакта  с  траекториями  системы  (1)  и  в  точках  этого  отрезка  будет  также  выполняться  неравенство:  .

Далее,  рассмотрим  однопараметрическое  семейство  прямых  линий    с  параметром  ,  меняющимся  в  пределах  -<k<0.  Если  все  прямые  семейства  касаются  некоторой  определенной  кривой  ,  то  эта  кривая  называется  огибающей  семейства  прямых.  Прямые  называются  огибаемыми. 

Поскольку  ,  то  у  нашего  семейства  прямых  нет  особых  точек  и,  следовательно,  огибающая    существует.  Пусть    –  координаты  точки  прикосновения  с  огибаемой  прямой,  соответствующей  значению  параметра  .

Взяв  производную  по  параметру  ,  получим: 

Учитывая,  что  ,  находим,  что  все  точки  прикосновения  подвижной  прямой  с  огибающей  ,  удовлетворяют  системе  уравнений:

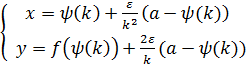    (5)

Таким  образом,  мы  получили  параметрическое  уравнение  огибающей  . 

Рассуждая  абсолютно  аналогично,  находим  параметрическое  уравнение  огибающей    семейства  касательных  прямых  =0,  0<k<:

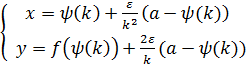  (6)

Далее  сформулируем  и  докажем  следующую  лемму:

Лемма  2.   Кривые    и    являются  кривыми  без  контакта  с  траекториями  системы  (1). 

Доказательство.   Рассмотрим  кривую  .  Предположим,  что  существует  значение  параметра  ,  при  котором  траектория  системы  (1)  касается  кривой    в  точке  ,  где  ,  .  Легко  убедиться,  что  касательная  к  кривой    в  точке    есть  прямая  =0.  Действительно,  имеем:  ,    и,  следовательно,  .  Но    есть  угловой  коэффициент  прямой  =0.  Ясно,  что  точка    не  совпадает  с  точкой  касания  изоклины    с  векторным  полем  системы  (1).  Значит  отрезок  прямой  =0,  проходящий  через  точку  ,  не  содержащий  точки  ,  является  отрезком  без  контакта  с  траекториями  системы  (1).  Следовательно,  огибающая    в  некоторой  окрестности  точки    также  является  кривой  без  контакта  с  траекториями  системы  (1).  Мы  пришли  к  противоречию.  Абсолютно  аналогично,  показывается,  что  кривая    является  кривой  без  контакта  с  траекториями  системы  (1).  Лемма  доказана. 

Далее  сформулируем  и  докажем  следующую  лемму:

Лемма  3.   Кривая  является  графиком  некоторой  убывающей  на  всей  числовой  оси,  выпуклой  книзу  функции  ,  а  кривая    является  графиком  некоторой  возрастающей  на  всей  числовой  оси,  выпуклой  книзу  функции  . 

Доказательство.  Как  уже  было  показано  выше,  в  точках  кривой    (конечное  отрицательное  число),  поэтому    есть  график  некоторой  убывающей  на  всей  числовой  прямой  функции  .  Аналогично,  так  как  в  точках  кривой  :    (конечное  положительное  число),  то    есть  график  некоторой  возрастающей  на  всей  числовой  прямой  функции  .  Докажем  выпуклость  книзу  обеих  функций.  Исследуем  значение  второй  производной    в  произвольной  точке    ,  которой  соответствует  значение  параметра  <0. 

Вторая  производная  . 

Т.  к.    (учитывая  равенство  (2)),  ,  ,  то    ,  откуда  следует,  что    ,  а  значит    выпуклая  книзу  функция. 

Аналогично  в  произвольной  точке  кривой    ,  которой  соответствует  значение  параметра  ,  вторая  производная  имеет  вид:

.

Т.  к.  ,  ,  ,  то 

,  откуда  следует,  что  ,  а  значит  .  Лемма  доказана. 

Далее  сформулируем  и  докажем  еще  одну  лемму:

Лемма  4.  В  точках  кривой    векторное  поле  направлено  наружу  (это  значит,  что  в  каждой  точке    кривой    наклон  векторного  поля    больше  соответствующей  производной  ),  а  в  точках  кривой    векторное  поле  направлено  вовнутрь  (это  значит,  что  в  каждой  точке    кривой    наклон  векторного  поля    меньше  соответствующей  производной  ). 

Доказательство.   Т.  к.  обе  кривые    и    располагаются  ниже  медленной  кривой  ,  то  наклон  векторного  поля  меняется  непрерывно  при  переходе  от  одной  точки  кривой  ()  к  другой.  Т.  к.  мы  уже  показали,  что  кривые    и    являются  кривыми  без  контакта  с  траекториями  системы(1),  то  достаточно  взять  две  точки,  одну  на  кривой  ,  другую  на  кривой    и  посмотреть,  как  будет  направлено  векторное  поле  в  этих  точках.  Если  в  одной  из  выбранных  точек  векторное  поле  будет  направлено  наружу  (вовнутрь),  то  и  во  всех  точках  соответствующей  кривой  векторное  поле  будет  направленно  наружу  (вовнутрь).  Возьмем  на  кривой    точку,  соответствующую  значению  параметра  .  Как  нетрудно  заметить,  в  этой  точке  кривая    пересекает  изоклину  горизонтальных  наклонов,  вертикальную  прямую  x=a.  Векторное  поле  в  этой  точке  имеет  нулевой  наклон,  а  соответствующая  производная  ,  значит  в  нашей  точке  векторное  поле  направлено  наружу,  следовательно,  во  всех  точках  кривой    векторное  поле  направлено  наружу. 

Возьмем  на  кривой    точку,  соответствующую  значению  параметра  .  В  этой  точке  кривая    пересекает  изоклину  горизонтальных  наклонов  x=a.  Векторное  поле  в  этой  точке  имеет  нулевой  наклон,  а  соответствующая  производная  ,  значит  в  рассматриваемой  точке  векторное  поле  направлено  вовнутрь,  следовательно,  и  во  всех  других  точках  кривой    векторное  поле  будет  направлено  вовнутрь.  Лемма  доказана.

Т.  к  кривые    и    являются  графиками  всюду  убывающей  на  числовой  прямой,  выпуклой  книзу  функции    и  всюду  возрастающей  на  числовой  прямой  выпуклой  книзу  функции    соответственно,  то  они  пересекаются  в  одной  точке  ,  которой  соответствуют  два  значения  параметра  :  ,  как  точке,  лежащей  на  кривой    и  ,  как  точке  лежащей  на  кривой  .  Значения  параметров    и    могут  быть  найдены  численно  с  заданной  точностью.

Теперь  введем  в  рассмотрение  следующую  кривую  :

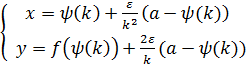  ,  где  параметр    (7)

Как  нетрудно  видеть,  это  кривая  при    совпадает  с  кривой  ,  а  при    совпадает  с  кривой  .  Именно  эту  кривую  мы  в  нашей  статье  предлагаем  в  качестве  приближения  траекторий-уток  системы  (1)  на  участке  их  движения  вдоль  медленной  кривой  (здесь  предполагается,  что  мы  уже  каким-либо  образом  «нащупали»,  с  некоторой  степенью  точности,  значение  параметра  ,  отвечающее  траекториям-уткам,  и  именно  это  значение  входит  в  параметрическое  задание  кривой  ). 

Если  быть  точнее,  то  в  качестве  приближения  пучка  траекторий-уток,  движущихся  вдоль  медленной  кривой  на  отрезке  [],  который  содержит  точку  минимума    медленной  кривой  (этот  отрезок  может  быть  сколь  угодно  большой  длины)  предлагается  взять  кривую  :

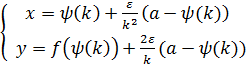  ,  где  параметр    (8)

Параметр    соответствует  точке  кривой    с  абсциссой  .  Он  может  быть  найден  численно  с  заданной  точностью,  как  отрицательный  корень  уравнения  .  Параметр    соответствует  точке  кривой    с  абсциссой  .  Он  может  быть  найден  численно  с  заданной  точностью,  как  положительный  корень  уравнения  .

Нетрудно  заметить,  что  кривая  ,  дает  оценку  отклонения  пучка  траекторий-уток,  от  медленной  кривой.  На  фазовой  плоскости  (x,y)  пучок  траекторий-уток  проходит  выше  данной  кривой.  Действительно,  траектория-утка  из  пучка  двигаясь  на  отрезке    не  может  пересечь  кривую  ,  в  силу  того,  что  векторное  поле  в  точках  кривой  на  этом  отрезке  направлено  вовнутрь.  Она  также  не  может  пересечь  кривую    двигаясь  на  отрезке    (в  противном  случае,  в  силу  очень  быстрого  изменения  наклона  векторного  поля  в  окрестности  кривой  ,  она  быстро  уйдет  влево  и  далее,  в  силу  того,  что  векторное  поле  в  точках  кривой    на  отрезке    направлено  наружу,  не  сможет  вновь  пересечь  эту  кривую  и  попасть  в  окрестность  медленной  кривой). 

Далее  сформулируем  и  докажем  следующую  теорему: 

Теорема  1.   Кривая    приближает  пучок  траекторий-уток,  движущихся  вдоль  медленной  кривой  на  отрезке  ,  с  порядком  O()  при  ε→  0. 

Доказательство.   Из  первого  уравнения  системы  (8)  можно  получить  следующие  соотношения:    ,    (здесь  мы  уже  рассматриваем  абсциссы  точек  касания  изоклин  с  векторным  полем  и  абсциссы  точек  кривой  ,  как  функции  двух  аргументов:  ).  Подставив  эти  выражения  во  второе  уравнение  системы  (8)  получим  следующее  соотношение:

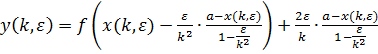  (здесь  мы  рассматриваем  ординаты  точек  кривой  ,  как  функции  двух  аргументов:  ).

Далее  введем  в  рассмотрение  следующие  функции  трех  аргументов: 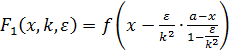   ,    и  .  Используя  формулу  Тейлора,  мы  можем  записать  следующие  соотношения:

.

Имеем: 

  -    ,  следовательно, 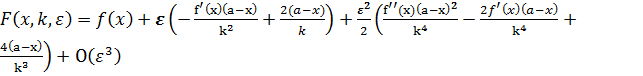   (9)

Далее,  введем  в  рассмотрение  следующую  функцию  четырех  аргументов: 

.

Используя  формулу  Тейлора,  мы  можем  записать  следующее  соотношение: 

.

Т.  к.  ,

,  то  .

Тогда  для  точек  кривой    имеем: 

,  а  т.  к.

,  то  можем  записать 

  (10)

Далее,  учитывая  (10),  имеем:

  (11)

  (12).

Учитывая  (9),  (10),  (11),  (12)  и,  что  для  ординат  точек  кривой    имеет  место  равенство  ,  упрощая  и  приводя  подобные  члены,  в  итоге  получим  для  кривой    следующее  асимптотическое  разложение:

  (13)

или  если  не  указывать  зависимость  точек  кривой    от  параметров 

  (14) 

С  другой  стороны,  для  траекторий-уток  системы  (1)  известны  следующие  результаты  (см.  [1]).  Все  значения  параметра  ,  соответствующие  траекториям-уткам,  имеют  одно  и  то  же  асимптотическое  разложение  по  степеням  ε.  Аналогичное  утверждение  справедливо  и  для  самих  траекторий-уток:  на  участке  движения  вдоль  медленной  кривой  они  имеют  одно  и  то  же  асимптотическое  разложение  по  степеням  ε.  Далее  воспользуемся  результатами  из  статьи  [1],  где  приводится  алгоритм  вычисления  коэффициентов  асимптотического  разложения  значений  параметра  ,  соответствующих  траекториям-уткам  системы  (1)  и  алгоритм  вычисления  коэффициентов  асимптотического  разложения  самих  траекторий-уток  на  участке  их  движения  вдоль  медленной  кривой.

Выпишем  эти  асимптотические  разложения,  ограничившись  первыми  тремя  членами  разложения:    (15)    (16)  ,  где  ,    ,    ,    ,   

Учитывая  данные  равенства,  мы  можем  записать  асимптотическое  разложение  кривой    в  следующем  виде: 

  (17)

Сравнивая,  равенства  (16)  и  (17),  видим,  что  асимптотическое  разложение  кривой    совпадает  с  асимптотическим  разложением  траекторий-уток  вплоть  до  второго  члена.  Покажем,  что  в  общем  случае  третьи  члены  не  совпадают.  Рассмотрим,  например,  функцию  (она  удовлетворяет  всем  требованиям,  накладываемым  на  функцию).  Тогда  в  разложении  (17)  кривой    коэффициент  при    будет  равен    ,  а  в  разложении  (16)  ,  соответствующем  траекториям-уткам  коэффициент  при    будет  равен  нулю.  Таким  образом,  кривая    приближает  пучок  траекторий-уток,  движущихся  вдоль  медленной  кривой  на  отрезке    ,  с  порядком  O().  Теорема  доказана. 

Список  литературы:

1. Арнольд  В.И.  и  др.  Теория  Бифуркаций.  Итоги  науки  и  техники.  Современные  проблемы  математики,  т.  1.  —  1986.
2. Звонкин  А.К.,  Шубин  М.А.  Нестандартный  анализ  и  сингулярные  возмущения  обыкновенных  дифференциальных  уравнений.  Успехи  математических  наук,  —  т.  39,  —  вып.  2.  —  1984.  —  с.  77—122. 
3. Benoit  E.,  Callot  J.-L.,  Diener  F.,  Diener  M.  Chase  au  canard.  —  Collecctaneu  Mathematica.  —  1980,  31:3.