МЕМБРАНЫ  В  МНОГОМЕРНОМ  ПРОСТРАНСТВЕ

Пешкичев  Юрий  Афанасьевич

канд.  физ.-мат.  наук,  исследователь, 
РФ,  г.  Бердск

E-mail: 

MEMBRANE  IN  A  MULTIDIMENSIONAL  SPASE

Yuriy  Peshkichev

candidate  of  Physical  and  Mathematical  Sciences, 
Russia,  Berdsk

АННОТАЦИЯ

Моделируются  виртуальные  движения  мембран  на  основе  рассмотрения  связанных  с  ними  скалярных  полей.

ABSTRACT

Simulated  virtual  movement  of  the  membranes  based  on  the  consideration  of  the  associated  scalar  fields.

Ключевые  слова:  плосковыпуклая  линза;  веретенообразная  область;  скалярное  поле;  поверхность  уровня.

Keywords:  plano-convex  lens;  fusiform  region;  scalar  field;  surface  level.

В  современной  теоретической  физике  рассматриваются  колебания  струн  и  мембран  в  многомерном  пространстве.  При  этом  до  последнего  времени  не  были  задействованы  результаты  по  геометрической  теории  скалярного  поля  в  многомерном  евклидовом  пространстве.  С  целью  устранения  наметившейся  диспропорции  в  статье  моделируется  виртуальное  движение  мембран  на  основе  связанных  с  ними  скалярных  полей.  При  этом  используется  новая  методика  исследования  гладкого  скалярного  поля,  разработанная  автором  в  книге  [5].  В  трёхмерном  пространстве  порождающее  скалярное  поле  можно  выбрать  так,  что  получится  фаза  реального  колебания  мембраны.  Струна  рассматривается  как  предельный  случай  мембраны  веретенообразного  типа.  Общее  понятие  о  струнах  и  мембранах  здесь  достаточно  представлять  по  книге  С.  Габсера  [2].  Примеры  же  современного  математического  подхода  к  колебаниям  мембран  содержатся  в  статье  Г.М.  Глинского  [3].  А  необходимые  для  доказательств  сведения  по  вещественному  анализу  содержатся  в  лекциях  Б.М.  Макарова  и  его  соавтора  А.Н.  Подкорытова  [4]. 

1.  Плосковыпуклая  линза  как  заметаемая  область  В  многомерном  евклидовом  пространстве  ℝⁿ  c  декартовыми  координатами  x₁,  x₂,…,x_n  рассмотрим  также  цилиндрические  координаты  (ρ,  φ,  z),  где  z  =  x_n  и  (ρ,  φ)  —  сферические  координаты  в  гиперплоскости  x_n  =  0.  Линзой  в  многомерном  пространстве  ℝⁿ  назовём  открытую  область 

G  =  {xℝⁿ:  ρ  <  1,  0  <  z  <  g(ρ)},

где  g(ρ)  —  гладкая  функция  на  отрезке  0  ≤  ρ  <1,  убывающая  на  нём  до  нуля.  Основанием  линзы  G  служит  диск

Ω  =  {x  ℝⁿ  :  ρ  <  1,  z  =  0}.

Верхней  же  поверхностью  введённой  линзы  G  является  гиперповерхность

S  =  {xℝⁿ:  ρ  <  1,  z  =  g(ρ)}.

Рассмотрим  в  области  G  гладкое  скалярное  поле 

u(M)  = 

c  нулевым  граничным  значением  на  основании  Ω  и  единичным  граничным  значением  на  верхней  поверхности  S,  для  которого  поверхность  уровня  u^-1(r)  гомеоморфна  основанию  Ω.  При  увеличении  параметра  r  от  нуля  до  единицы  рассматриваем  теперь  гиперповерхности  u^-1(r)  как  положения  m(r)  мембраны  ρ  при  её  виртуальном  движении  из  исходного  положения  Ω  в  конечное  положение  S.  Линза  G  представляет  тогда  собой  заметаемую  мембраной  часть  пространства  ℝⁿ.  В  случае  реальных  малых  колебаний  круглой  мембраны  в  физическом  пространстве  одна  из  стоячих  волн  порождается  скалярным  полем

u(M)  =  arcсos    ,

где:  ,  J()  —  функция  Бесселя  первого  рода  порядка  ноль, 

  —  её  первый  корень, 

  —  малое  положительное  число.  Геометрическая  теория  функций  предлагает  несколько  числовых  характеристик  виртуального  движения  мембраны,  использование  здесь  которых  основано  на  интегральном  свойстве  градиента  скалярного  поля

известном  как  теорема  о  послойном  интегрировании  (криволинейная  теорема  Фубини,  теорема  А.С.  Кронрода-Г.  Федерера  [4,  c.  391]).  Процесс  виртуального  движения  мембраны  характеризуется  интегралом  Дирихле

D(u,G)  =  ⁿdG.

При  этом  проявляется  след  интеграла  Дирихле  на  поверхности  уровня  скалярного  поля

для  которого  по  теореме  о  послойном  интегрировании  выполняется  равенство 

D(u,G)  = 

Упомянутый  процесс  виртуального  движения  мембраны  характеризуется  также  модулюсом  ModΣ  семейства  Σ  всех  поверхностей  уровня  u^-1(r),  где

ModΣ  =  inf  ⁿdG,

а  весовая  функция  берётся  здесь  точная  нижняя  грань,  для  почти  всех  значений  r  (0,1)  обладает  свойством 

Формально  весовая  функция  является  скалярным  полем,  однако  без  требования  гладкости  и  без  рассмотрения  его  градиента.  Особую  роль  в  определении  модулюса  играет  экстремальная  весовая  функция

(М)  =  |gradu|/D(u,G,r)^1/(n-1).

В  самом  деле,  так  как  для  почти  всех  значений  r  (0,1)  выполняется  неравенство

то  по  теореме  о  послойном  интегрировании  получается  верхняя  оценка

ModΣ  ≤  (M)ⁿdG  =

=^1/(1-n)dr.

C  другой  же  стороны,  для  всякой  допустимой  в  определении  модулюса  функции  (М)  при  почти  всех  значениях  r    (0,1)  будет

что  следует  из  тождества

(М)    |gradu|^1/n(M)/|gradu|^1/n

после  применения  неравенства  Гёльдера  к  поверхностному  интегралу

По  теореме  о  послойном  интегрировании

(М)ⁿdG  ≥  ^1/(1-n)dr.

В  результате  у  нас  получается  вычислительная  формула  для  модулюса

ModΣ  =  ^1/(1-n)dr.

Виртуальное  движение  мембраны  можно  охарактеризовать  также  ещё  интегралом  кривизны  скалярного  поля  u(M)  в  области  G

J(u,G)  =  ^n/(n-1)dG,

где:  k  —  полная  кривизна  поверхности  уровня  u^-1(r)  в  точке  М  u^-1(r).

Теорема.  Если  рассмотреть  гауссово  изображение  N(r)  поверхности  уровня  u^-1(r)  на  сфере  единичного  радиуса  в  ℝⁿ,  то

J(u,G)^n-1D(u,G)  ≥  (  _n-1N(r)dr)ⁿ.

Доказательство.  Так  как  полная  кривизна  поверхности  уровня  u^-1(r)  служит  касательным  якобианом  гауссового  отображения

N:  u^-1(r)  {x  ℝⁿ:  |x|  =  1},

то  для  почти  всех  значений  r  (0,1)  выполняется  неравенство

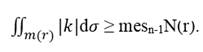
По  теореме  о  послойном  интегрировании  тогда

_n-1N(r)dr  ≤    |k|dG.

Далее  остаётся  применить  неравенство  Гёльдера  в  кратном  интеграле.

2.  Веретенообразная  область  заметания

Пусть  теперь  открытая  область  G  в  ℝⁿ,  заметаемая  мембраной  при  её  виртуальном  движении,  ограничена  поверхностью  вращения    =  g(|z|).  Упомянутое  вращение  происходит  вокруг  оси  координат  Ox_n  в  случае  нечётного  числа  n.  Тогда  область  G  будет  задана  условием

G  =  {x  ℝⁿ:  0  <  |z|  <  1,    <  g|(z|)}.

Стержнем  области  G  назовём  отрезок

L  =  {x  ℝⁿ:  |z|  <  1,    =0}.

При  этом  поверхность  веретенообразной  области  G  задаётся  условием

S  =  {xℝⁿ:  0  <|z|  <  1,    =  g(|z|)}.

Рассмотрим  в  области  G  гладкое  скалярное  поле

u(M)  = 

c  нулевым  граничным  значением  на  стержне  L  и  единичным  граничным  значением  на  поверхности  S.  При  этом  все  поверхности  уровня  u^-1(r)  гомеоморфны  поверхности  S,  кроме  значения  r  =  0,  когда  поверхность  уровня  сворачивается  в  стержень  L.  При  увеличении  параметра  r  от  нуля  до  единицы  мембрана  m(r)  совершает  виртуальное  движение  из  своего  сингулярного  положения  L  в  обычное  положение  S.  Используя  теперь  терминологию  книги  [2,  c.  136],  мы  отмечаем  новый  тип  сворачивания  D(n-1)  —  браны  в  D1  —  брану.  Виртуальное  движение  рассмотренного  типа  мембран  можно  так  же  охарактеризовать  перечисленным  в  п.  1  набором  числовых  характеристик.  В  физическом  трёхмерном  пространстве  такой  тип  колебаний  мембраны,  скорее  всего,  вообще  не  рассматривался.

3.  Заполненный  тор  вращения  с  (n-1)  —  мерным  сечением  в  форме  серповидной  линзы  как  заметаемая  область

Для  катеноида  в  ℝⁿ,  имеющего  уравнение  (|z|),  рассмотрим  открытую  область 

G  =  {xℝⁿ:  |z|  <  a,    (|z|)<  +  g(|z|/a)},

где  функция  (t)взята  из  п.  1.  Для  4≤n≤26  приведённое  определение  будет  корректно  при  достаточно  малом  значении  а  >  0  [1].  Затем  порождающее  скалярное  поле  определяем  формулой

u(M)  =  1/(1  +  g(|z|/a)/(|z|)).

Тогда  при  увеличении  параметра  r  от  нуля  до  единицы  гиперповерхность  u^-1(r)  совершает  виртуальное  движение  из  положения  на  катеноиде  до  своего  предельного  возмущённого  положения.  В  физическом  трёхмерном  пространстве  катеноид  как  мембрана  рассмотрен  в  работе  [3],  где  для  него  получено  дифференциальное  уравнение  колебаний. 

Список  литературы:

1. Веденяпин  А.Д.,  Миклюков  В.М.  Внешние  размеры  трубчатых  минимальных  гиперповерхностей  //  Математ.  сб.  —  1986.  —  Т.  131  (173).  —  №  2(10).  —  С.  240—250.
2. Габсер  С.  Маленькая  книга  о  большой  теории  струн.  —  СПб.  :  Питер,  2015.  —  208  с.
3. Глинский  Г.М.  К  теории  малых  колебаний  произвольно  искривлённых  мембран  //  ЖТФ.  —  2000.  —  Т.  70.  —  Вып.  1.  —  С.  10—14.
4. Макаров  Б.М.  Лекции  по  вещественному  анализу  /  Б.М.  Макаров,  А.Н.  Подкорытов.  —  СПб.:  БХВ  –  Петербург,  2011.  —  688  с.
5. Пешкичев  Юрий.  Кривизна  в  теории  поля.  Скалярные  и  векторные  поля  на  плоскости  и  в  многомерном  пространстве.  LAP  LAMBERT  Academic  Publishing  (2015.04.15).  —  104  c.