КОНЕЧНАЯ  СКОРОСТЬ  РАСПРОСТРАНЕНИЯ  ВОЗМУЩЕНИЙ  ДЛЯ  НЕЛИНЕЙНЫХ  ВЫРОЖДАЮЩИХСЯ  ПАРАБОЛИЧЕСКИХ  УРАВНЕНИЙ  С  КОНВЕКТИВНЫМ  ЧЛЕНОМ

Семенко  Евгений  Вениаминович

д-р  физ.-мат.  наук,  зав.  кафедрой  математического  анализа,  профессор  Новосибирского  государственного  педагогического  университета,  РФ,  г.  Новосибирск

E-mail:  semenko

Семенко  Татьяна  Ивановна

канд.  физ.-мат.  наук,  доцент  Новосибирского  государственного  педагогического  университета,  РФ,  г.  Новосибирск

E-mail: 

A  FINITE  SPEED  OF  DISTURBANCES  PROPAGATION  FOR  NONLINEAR  DEGENERATE  PARABOLIC  EQUATIONS  WITH  CONVECTIVE  TERM

Evgeny  Semenko

doctor  of  science,  head  of  mathematical  analysis  department,  professor  of  Novosibirsk  State  Pedagogical  University,  Russia,  Novosibirsk

Tatyana  Semenko

c andidate  of  science,  assistant  professor  of  Novosibirsk  State  Pedagogical  University,  Russia,  Novosibirsk

АННОТАЦИЯ

Доказано  наличие  конечной  скорости  распространения  возмущений  от  начальных  данных  для  нелинейных  вырождающихся  параболических  уравнений  с  конвективным  членом.  Для  доказательства  использован  модифицированный  метод  интегральных  энергетических  оценок,  основанный  на  интегрировании  уравнения  по  нецилиндрической  по  времени  области. 

ABSTRACT

The  existence  of  finite  speed  of  initial  data  disturbances  propagation  for  degenerate  nonlinear  parabolic  equations  with  convective  transport  is  proved.  The  modified  method  of  integral  energy  estimation  based  on  the  integration  over  the  noncylindrical  region  is  used  for  proving. 

Ключевые  слова:  нелинейные  вырождающиеся  параболические  уравнения;  конечная  скорость  распространения  возмущений;  метод  энергетических  оценок. 

Keywords:  nonlinear  degenerate  parabolic  equations;  finite  speed  of  disturbances  propagation;  energy  estimation  method.

Вырождающиеся  нелинейные  параболические  уравнения  широко  используются  в  моделях  фильтрации  с  массопереносом.  Одним  из  таких  уравнений  является  уравнение  Ричардса,  используемое  при  моделировании  процесса  насыщенно-ненасыщенной  фильтрации  [5],  [6],  [8].  К  возможным  особенностям  поведения  решений  вырождающихся  параболических  уравнений,  которые  нужно  учитывать  в  том  числе  и  при  реализации  численных  алгоритмов,  относится  конечная  скорость  распространения  возмущений  от  начальных  данных. 

Вопросам  конечной  скорости  для  вырождающихся  параболических  уравнений  посвящено  множество  работ.  Первые  результаты  в  этой  области  получены  для  одномерных  уравнений  с  гладкими  коэффициентами  на  основе  теорем  сравнения.  Достаточно  полная  библиография  и  обзор  таких  работ  приведены  в  [1].  Для  общих  параболических  и  эллиптических  уравнений  с  суммируемыми  коэффициентами  используется  метод  интегральных  энергетических  оценок,  предложенный  Антонцевым  С.Н.  в  [1],  [2]  и  получивший  дальнейшее  развитие  в  [3],  [4],  [7]  и  других  работах.  Метод  основан  на  интегрировании  уравнения  по  пространственно-временной  области,  цилиндрической  по  времени.  В  результате  устанавливается,  что  решение  в  такой  области  при  нулевых  начальных  данных  будет  равно  нулю  в  течение  некоторого  достаточно  малого  времени,  что  и  означает  конечную  скорость.  Однако  предложенный  метод  плохо  приспособлен  для  уравнений  с  конвективным  членом,  то  есть  для  моделей,  учитывающих  массоперенос.  Для  таких  уравнений  в  [4]  установлена  конечная  скорость  при  очень  жестких  условиях  подчиненности  конвективного  члена  вырождающемуся  диффузионному.  Это  условие  представляется  неестественным,  поскольку  даже  при  отсутствии  диффузионного  члена  решение  уравнения  переноса  имеет  конечную  скорость. 

В  данной  работе  предлагается  видоизмененный  вариант  метода  интегральных  оценок,  отличающийся  от  используемых  ранее  тем,  что  для  получения  основного  интегрального  неравенства  применяется  интегрирование  по  нецилиндрической  по  времени  области,  в  которой  начальные  данные  равны  нулю,  с  таким  расчетом,  чтобы  исключить  массоперенос  в  эту  область  ненулевых  начальных  данных  извне.  Это  позволяет  доказать  конечную  скорость  распространения  возмущений  при  отсутствии  связи  между  диффузионным  и  конвективным  членами. 

Перейдем  к  точным  формулировкам.  В  области  =где  ,  mes    рассмотрим  уравнение 

где:  искомая)  функция  переменных  и  ,    —  время;

  —  скалярная  функция,  определенная  в 

  и    —  n-мерные  векторные  функции,  определенные  в  и  соответственно;

  ,

где  –  -тая  компонента  функции 

В  правой  части  уравнения  (1)  первое  слагаемое  представляет  собой  диффузионный  член,  а  второе  –  конвективный. 

Пусть  для  всех    выполнены  следующие  условия:

функция    непрерывна,  монотонна  по    при  всех  ,

где  ,    —  неотрицательные  постоянные.  Здесь  (3)  и  (4)  —  это  условия  того,  что  уравнение  (1)  является  вырождающимся  параболическим. 

Определение.   Обобщенным  решением  уравнения  (1),  удовлетворяющим  начальному  условию  ,  назовем  функцию    определенную  в    такую,  что 

и  для  любой  функции    ,  для  почти  всех    выполнено:

+

+=

+.

Теорема.  Пусть  выполнены  условия  (2)—(6),  где 

а    —  обобщенное  решение  уравнения  (1)  в  удовлетворяющее  начальному  условию  ,  где    при 

замыкание  множества    включается  в    >0.  Тогда  для  любого    существует  время    такое,  что   

при  ,    ,  где    зависят  от  параметров  в  условиях  (2)–(6),  а  ,  кроме  того,  и  от  .

Замечание.  Отметим,  что    и    здесь  не  связаны  с  .  Это  означает,  что  конвективный  член  никак  не  связан  с  диффузионным. 

Доказательство  теоремы.  Пусть    угол,  такой,  что 

,

а    —  произвольное  пока  число,  .  Для  любых  ,    будем  рассматривать  усеченные  конусы 

,

где  .  Угол    выбран  с  таким  расчетом,  чтобы  в  конус    не  попадали  характеристики  уравнения  переноса,  выходящие  из  точек  ,  расположенных  вне  .

Введем  следующие  обозначения: 

  —  сечение    плоскостью 

;    —  граница 

=  —  боковая  поверхность  конуса  ;  ;    , 

Имеют  место  соотношения:  ,  где    —  дифференциальная  форма  на  сфере  , 

Легко  видеть,  что  ,  и  выполнено  следующее  неравенство: 

Оценим  правую  часть  (9),  применяя  (3)  и  неравенство  Гельдера:

Далее  воспользуемся  следующим  неравенством  из  [9]: 

  ,

где   

Имеем: 

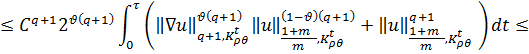
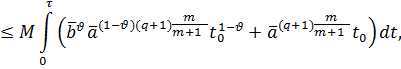
где  .

Пусть    =

Тогда,  так  как  ,  то 

,  где  .

Следовательно,  ,  где  .

Введём  далее  следующие  обозначения: 

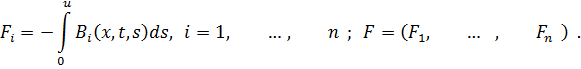
Левую  часть  (9),  которая  в  новых  обозначениях  примет  вид 

  +,

преобразуем  с  использованием  формулы  Стокса  и  условия,  что  ,  если    к  виду:

  +

.

Далее,  +

откуда,  в  силу  выбора  ,  следует,  что   

Предположим  теперь,  что  ,  где    . 

Тогда  . 

Суммируя  оценки  для    ,  получим:

Применим  неравенство  Юнга  к  (10):

  ,

где  . 

Следовательно,  +  . 

Пусть    ,  ,    ,  Тогда  имеем:

,  откуда,  аналогично  [4],  получим  неравенство 

,  из  которого  вытекает,  что 

  при    ,  откуда  и  следует  утверждение  теоремы. 

Следствие.  Пусть  выполнены  все  предположения  теоремы.  Тогда  для  любого    существует  время  ,  зависящее  от    и  постоянных  в  условиях  (2)—(6),  такое,  что    при    ,  . 

Этот  факт  и  означает  наличие  конечной  скорости  распространения  возмущений  от  начальных  данных.

Список  литературы:

1.Антонцев  С.Н.  О  характере  возмущений,  описываемых  решением  многомерных  вырождающихся  параболических  уравнений  //  Динамика  сплошной  среды.  —  1979.  —  вып.  40.  —  C.  114—122.

2.Антонцев  С.Н.  Конечная  скорость  распространения  возмущений  в  многомерных  задачах  двухфазной  фильтрации  //  Зап.  науч.  семинаров  ЛОМИ  АН  СССР.  —  1980.  —  т.  96.  —  C.  2—12.

3.Антонцев  С.Н.  О  локализации  решений  нелинейных  вырождающихся  эллиптических  и  параболических  уравнений  //  Докл.  АН  СССР.  —  1981.  —  т.  260,  —  №  6.  —  C.  1289—1293.

4.Антонцев  С.Н.  Локализация  решений  вырождающихся  уравнений  механики  сплошной  среды.  Новосибирск:  ИГиЛ  СОАН  СССР,  1986.  —  108  с.

5.Антонцев  С.Н.,  Кашеваров  А.А.,  Ускова  Т.И.  Приближенная  гидравлическая  модель  взаимодействия  грунтовых  вод  с  зоной  неполного  насыщения  //  Динамика  сплошной  среды.  —  1986.  —  вып.  76.  —  С.  19—31.

6.Антонцев  С.Н.,  Кашеваров  А.А.,  Семенко  Т.И.  Итерационный  метод  решения  стационарной  задачи  о  насыщенно-ненасыщенной  фильтрации  в  гидравлическом  приближении  //  Динамика  сплошной  среды.  —  1989.  —  вып.  90.  —  С.  3—15.

7.Палымский  И.Б.  Некоторые  качественные  свойства  решений  уравнений  нелинейной  теплопроводности  с  поглощением  //  Численные  методы  механики  сплошной  среды.  —  1985.  —  т.  16,  —  №  1.  —  С.  136—145.

8.Семенко  Т.И.  О  корректности  приближенной  гидравлической  модели  насыщенно-ненасыщенной  фильтрации  //  Динамика  сплошной  среды.  —  1991.  —  вып.  102.  —  С.  114—132.

9.Ладыженская  О.А.,  Уральцева  Н.Н.  Линейные  и  квазилинейные  уравнения  эллиптического  типа.  М.:  Наука,  1973.  —  576  с.