МАТЕМАТИЧЕСКАЯ  МОДЕЛЬ  СОЛИДНОЙ  ОПУХОЛИ

Жукова  Ирина  Валерьевна

аспирант  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E-mail:  zhira428@mail.ru

Колпак  Евгений  Петрович

д-р  физ.-мат.  наук,  профессор  Санкт-Петербургского  государственного  университета,  РФ,  Санкт-Петербург

E-mail: 

MATHEMATICAL  MODEL  OF  SOLID  TUMOUR

Irina  Zhukova

post-graduate  student  of  St.  Petersburg  State  University,  Russia  St.  Petersburg

Eugeniy  Kolnak

doctor  of  Physics  and  Mathematics,  professor  of  St.  Petersburg  State  University,  Russia  St.  Petersburg

АННОТАЦИЯ

Разработана  математическая  модель  злокачественной  опухоли,  представляющая  собой  задачу  Коши  для  системы  обыкновенных  дифференциальных  уравнений.  Проанализирована  устойчивость  стационарных  решений,  построены  численные  решения.  Дана  оценка  влияния  химиотерапии  на  рост  опухоли.

ABSTRACT

Mathematical  model  of  cancer  tumour  which  represents  a  Cauchy  problem  for  system  of  ordinary  differential  equations  was  developed.  Stability  of  stationary  solutions  was  analyzed,  numerical  solutions  were  built.  Evaluation  of  chemotherapy’s  influence  on  tumor  growth  was  given. 

Ключевые  слова:  математическое  моделирование;  дифференциальные  уравнения.

Keywords:  mathematical  modeling;  differential  equations.

Новообразования  продолжают  оставаться  одним  из  менее  изученных  заболеваний  всех  млекопитающих,  включая  человека,  и  являются  одной  из  основных  причин  их  ранней  смертности.  В  России  около  15  %  всех  смертей  среди  населения  приходится  на  долю  онкологических  заболеваний.  По  мнению  специалистов,  злокачественные  новообразования  продолжают  оставаться  практически  неизлечимыми  [6,  с.  8—11].  Одним  из  подходов  в  поиске  эффективного  пути  лечения  является  математическое  моделирование.

Первые  математические  модели  злокачественной  опухоли  представляли  собой  задачу  Коши  для  системы  обыкновенных  дифференциальных  уравнений.  В  моделях  учитывались  опухолевые,  здоровые  и  погибшие  клетки,  питание,  различные  ингибирующие  вещества,  ответ  иммунной  системы  [15—17].  Затем  были  предложены  модели  типа  диффузия-адвекция-реакция,  в  которых  опухоль  рассматривалась  как  система  с  распределенными  параметрами  [2,  3,  12—14,  18—20].

Клетки  здорового  организма  смертны,  «запрограммированная»  смерть  (апоптоз)  является  окончанием  жизненного  цикл.  В  свою  очередь,  основной  особенностью  клеток  злокачественной  опухоли  является  отсутствие  апоптоза  [1,  6,  15,  17].  Поскольку  опухолевые  клетки  не  отличаются  от  здоровых,  то  иммунная  система  с  трудом  их  распознает  [15].  С  ростом  опухоли  ее  клетки  группируются,  образуя  различные  пространственные  структуры  (сфероиды,  трубки,  нити,  диски  и  т.  п.)  [6,  15].  Внутренние  клетки  образовавшейся  структуры  начинают  гибнуть  в  силу  недостаточного  питания,  внешние  опухолевые  клетки  продолжают  размножаться,  оттесняя  от  себя  здоровые  клетки.  В  процессе  роста  опухоли,  как  делящиеся  клетки,  так  и  все  погибшие  из  организма  не  выносятся,  образуя  «солидную»  опухоль  [6,  8,  9,  17].  Т.  е.,  злокачественная  опухоль  представляет  собой  независимое  образование  из  ядра  погибших  клеток,  окруженного  слоем  непрерывно  делящихся  клеток  опухоли.  В  силу  своей  автономности  к  окружающим  тканям,  опухолевые  клетки  проникают  в  окружающие  ткани,  разрушая  их  и  создавая  новые  точки  роста.

В  рассматриваемой  модели  опухоли  учитывается  три  типа  клеток:  непрерывно  делящиеся  (опухолевые),  нормальные  (здоровые)  и  погибшие  [14].  Предполагается,  что  апоптоз  у  делящихся  клеток  отсутствует.  Нормальные  клетки  в  отсутствие  делящихся  размножаются  по  логистическому  закону  [7].  В  процессе  роста  делящиеся  клетки  выделяют  токсичные  вещества,  оказывающие  ингибирующее  влияние  на  нормальные  клетки  [6,  8,  9,  17].  Погибшие  клетки  оказывают  ингибирующее  влияние  на  нормальные  и  делящиеся.  Ткань  опухоли  считается  мало  сжимаемой.  Поэтому  равновесные  концентрация  нормальных  клеток  в  отсутствие  делящихся  и  погибших  и  концентрация  погибших  в  отсутствие  делящихся  и  нормальных  должны  быть  одинаковыми  и  ниже  принимаются  равными  единице.

В  качестве  одного  из  методов  лечения  опухолей  является  химиотерапия  [6,  8,  9,  17].  В  рассматриваемой  модели  злокачественного  образования  на  нормальные  клетки  ингибирующее  влияние  оказывают  как  делящиеся  клетки,  так  и  погибшие.  Поэтому  в  модели  учитывается  «химиотерапия»  постоянного  воздействия  только  на  делящиеся  и  погибшие  клетки.

Пусть    —  количество  делящихся  клеток,    —  нормальных  клеток,    —  погибших.  С  учетом  введенных  обозначений  система  дифференциальных  уравнений,  описывающая  рост  «солидной»  опухоли,  имеет  следующий  вид:

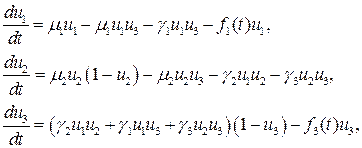                         (1)

В  первом  уравнении  слагаемое    —  скорость  «собственного»  роста  делящихся  клеток,  слагаемое    —  скорость  ингибирования  погибшими  клетками  делящихся,  слагаемое    —скорость  вытеснения  делящихся  клеток  погибшими.  Слагаемое    во  втором  уравнении  —  скорость  изменения  численности  нормальных  клеток,    —  скорость  ингибирования  делящимися  клетками  здоровых,    —  скорость  ингибирования  нормальных  клеток  погибшими,    —  скорость  вытеснения  нормальных  клеток  погибшими.  Скорость  роста  мертвых  клеток  (третье  уравнение  в  (1))  пропорциональна  .  Множитель    отражает  тот  факт,  что  заполнение  функционального  пространства,  занимаемого  погибшими  клетками,  происходит  тем  медленнее,  чем  больше  его  наполнение.  ,  ,  ,  ,    —  положительные  константы,  характеризующие  скорости  реакций.  Неотрицательные  функции    и    описывают  поступление  химических  препаратов,  влияющих,  соответственно,  на  скорость  роста  делящихся  клеток  и  на  скорость  накопления  погибших.  При  этом  предполагается,  что  скорость  гибели  делящихся  клеток  пропорциональна  их  концентрации  и  концентрации  химических  препаратов.  Это  же  предположение  относится  и  к  скорости  распада  погибших  клеток  при  действии  на  них  химиопрепаратов.

В  отсутствие  делящихся  и  погибших  клеток  из  уравнений  (1)  следует  уравнение  для  роста  нормальных  клеток    5,  7]

В  этой  модели  изменения  численности  нормальных  клеток  предполагается,  что  скорость  их  рождения  равна  ,  а  гибель  происходит  со  скоростью  .

В  качестве  начальных  условий  будут  рассматриваться  условия  при  :  ,  ,  ,  где    —  малая  величина.  Эти  начальные  условия  подразумевают,  что  в  начальный  момент  времени  в  функциональном  пространстве  нормальных  клеток  (погибшие  клетки  отсутствуют)  возникает  небольшое  количество  делящихся  клеток.

Система  уравнений  (1)  при    и    имеет  три  стационарные  точки

1.  ,  , 

2.  ,  , 

3.  ,  ,    —  любое. 

Третья  стационарная  точка  имеет  физический  смысл  только  в  том  случае,  если  .  В  первой  стационарной  точке  матрица  Якоби  правой  части  уравнений  (1)  имеет  собственное  значение  .  То  есть  эта  стационарная  точка  неустойчива  в  линейном  приближении.  В  малой  окрестности  второй  стационарной  точки  малые  возмущения  решения  ,    и    удовлетворяют  системе  уравнений

,

.

Решение  этих  уравнений  представляется  в  виде

,    ,

Возмущения    и    должны  быть  положительными  в  силу  физического  смысла  решения.  Поскольку    и    убывающие  по  модулю  функции,  стремящиеся  к    при  ,  то    возрастающей  функцией  времени  не  будет  и  малым  значением    будут  соответствовать  и  малые  значения    при  достаточно  больших  значениях  .  То  есть  это  положение  равновесия  будет  устойчивым.  Таким  образом,  в  рассматриваемой  модели  происходит  постепенное  вытеснение  нормальных  клеток  погибшими. 

Численное  решение  уравнений  (1)  осуществлялось  в  среде  математического  пакета  MatLab  [5]  с  использованием  встроенных  функций.  На  рис.  1  показано  изменение  функций  ,    и    (численное  решение  уравнений  (1))  во  времени  при  ,  ,  ,  ,  .  Как  следует  из  анализа  численных  результатов  концентрация  погибших  клеток  непрерывно  растет,  концентрация  делящихся  клеток  сначала  растет,  а  затем  начинает  убывать.  Концентрация  нормальных  клеток  монотонно  уменьшается.

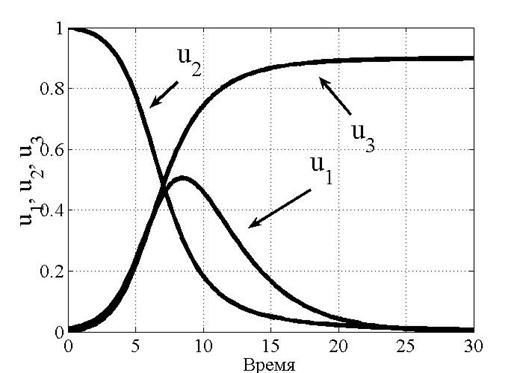
Рисунок  1.  Динамика  изменения  функций  ,  , 

При  наличии  химиотерапии  функции    и    задают  «программу  лечения».  Для  случая    и    стационарные  точки  системы  уравнений  (1)  находятся  как  положительное  решение  системы  алгебраических  уравнений

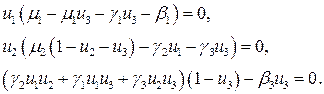
При    первое  уравнение  будет  удовлетворено  только  при  .  В  этом  случае  при    третье  уравнение  будет  удовлетворяться  только  при  .  Т.е.,  при  этих  условиях  реализуется  стационарная  точка  ,  ,  .  Собственные  значения  матрицы  Якоби  в  этой  стационарной  точке  ,  ,    будут  в  этом  случае  отрицательными  и,  соответсвенно,  стационарная  точка  будет  устойчивой.  Т.  о.,  для  уничтожение  делящихся  клеток  необходимо,  чтобы  скорость  их  уничтожения  была  больше  скорости  их  роста.  При  этом  возможно  и  уничтожение  погибших  клеток,  если  скорость  их  уничтожения  препаратами  будет  больше  скорости  их  накопления.

Список  литературы:

1.Акоев  И.Г.  Биофизика  познает  рак.  М.:  Наука,  1988.  —  160  с.

2.Астанин  С.А.,  Лобанов  А.И.  Трехмерная  модель  роста  неваскуляризированной  опухоли  в  ткани  //  Математика.  Компьютер.  Образование.  —  2005.  —  Ч.  1.  —  C.  759—769.

3.Астанин  С.А.,  Колобов  А.В.,  Лобанов  А.И.,  Пименова  Т.П.,  Полежаев  А.А.,  Соляник  Г.И.  Влияние  пространственной  гетерогенности  среды  на  рост  и  инвазию  опухоли.  Анализ  методами  математического  моделирования  //  Медицина  в  зеркале  информации.  М.:  Наука,  2008.  —  С.  188—223.

4.Балыкина  Ю.Е.,  Колпак  Е.П.  Введение  в  Matlab.  СПб:  Соло.  2013.  —  302  с.

5.Балыкина  Ю.Е.,  Колпак  Е.П.  Математические  модели  функционирования  фолликула  щитовидной  железы  //  Вест.  С.-Петерб.  ун-та.  Сер.  10:  Прикладная  математика,  информатика,  процессы  управления.  —  2013.  —  Вып.  3.  —  С.  20—31.

6.Васильев  Ю.М.  Биология  злокачественного  роста.  М.:  Наука.  1965.  —  180  с.

7.Горбунова  Е.А.,  Колпак  Е.П.  Математические  модели  одиночной  популяции  //  Вест.  С.-Петерб.  ун-та.  Сер.  10:  Прикладная  математика,  информатика,  процессы  управления.  —  2012.  —  Вып.  4.  —  С.  18—30.

8.Долгих  В.Т.  Опухолевый  рост:  учеб.  пособие/В.Т.  Долгих.  Ростов  н/Д.:  Феникс,  2007.  —  160  с.

9.Жимулев  И.Ф.  Общая  и  молекулярная  генетика.  Новосибирск:  Изд-во  Новосиб.  ун-та,  2002.  —  459  с.

10.Колбин  А.С.,  Курылев  А.А.,  Павлыш  А.В.,  Проскурин  М.А.,  Балыкина  Ю.Е.  Научный  анализ  исходов  в  онкологии.  Особенности  фармакоэкономической  экспертизы  //  Мед.  техн.  Оценка  и  выбор.  —  2012.  —  Т.  2  (8).  —  С.  87—93.

11.Колбин  А.С.,  Сидоренко  С.В.,  Балыкина  Ю.Е.  Исследования  в  области  новых  антибактериальных  средств  —  есть  ли  перспективы?  //  Педиатрическая  фармакология.  —  2010.  —  Т.  7.  —  №  5.  —  С.  12—16.

12.Колобов  А.В.,  Губернов  В.В.,  Полежаев  А.А.  Автоволны  в  модели  роста  инвазивной  опухоли  //  Биофизика.  —  2009.  —  Т.  54.  —  Вып.  2.  —  C.  334—342.

13.Колобов  А.В.,  Полежаев  А.А.  Влияние  случайной  подвижности  злокачественных  клеток  на  устойчивость  фронта  опухоли  //  Компьютерные  исследования  и  моделирование.  —  2009.  —  T.  1  —  №  2.  —  С.  225—232.

14.Колобов  А.В.,  Анашкина  А.А.,  Губернов  В.В.,  Полежаев  А.А.  Математическая  модель  роста  опухоли  с  учетом  дихотомии  миграции  и  пролиферации  //  Компьютерные  исследования  и  моделирование.  —  2009.  —  Т.  1.  —  №  4.  —  с.  415—422.

15.Моисеенко  В.М.,  Блинов  Н.Н.,  Хансон  К.П.  Биотерапия  при  злокачественных  новообразованиях  //  Российский  онкологический  журнал.  —  1997.  —  №  5.  —  C.  7—59.

16.Слепков  В.А.,  Суховольский  В.Г.,  Хлебопрос  З.Г.  Популяционная  динамика  в  моделировании  роста  раковых  опухолей  //  Биофизика.  —  2007.  —  Т.  52.  —  Вып.  4.  —  С.  733—740.

17.Эммануэль  Н.М.  Кинетика  экспериментальных  опухолевых  процессов.  М.:Наука,  1977.  —  419  с.

18.Byrne  H.M.,  Breward  C.J.W.,  Lewis  C.E.  The  role  of  cell-cell  interactions  in  a  two-phase  model  for  avascular  tumour  growth  //  Journal  of  Mathematical  Biology.  —  2001.  —  Vol.  45.  —  №  2.  —  P.  125—131. 

19.Chaplain  M.A.J.,  Sherratt  J.A.  A  new  mathematical  model  for  avascular  tumor  growth  //  Journal  of  Mathematical  Biology.  —  2000.  —  Vol.  43.  —  №  4.  —  P.  291—312.

20.Mohammed  Shuker  Mahmood,  Silvia  Mahmood,  Dusan  Dobrota  //  Formulation  and  numerical  simulations  of  a  continuum  model  of  avascular  tumor  growth  //  Mathematical  Biosciences.  —  2011.  —  Vol.  231.  —  №  2.  —  P.  159—171.