ПОВЫШЕНИЕ УСТОЙЧИВОСТИ АЛГОРИТМОВ РЕКОНСТРУКЦИИ ТОМОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ

Лавров Семен Александрович

инженер, РФЯЦ-ВНИИТФ, г. Снежинск

E-mail: semlav@list.ru

Как известно [3, 5] задача решения уравнения Радона является некорректно поставленной задачей, небольшие погрешности в проекционных данных могут привести к большим погрешностям в реконструируемой функции.

Методы повышения устойчивости алгоритмов реконструкции томографического изображения (метод усечения частот и метод Тихонова) могут быть недостаточными для повышения качества изображения, в особенности, когда проекционные данные являются достаточно зашумленными (влияние ошибок измерений электронной системы сбора данных, технических и физических факторов сканирующей системы томографического комплекса).

Одним из подходов для повышения устойчивости алгоритмов реконструкции является использование кратномасштабного анализа теории вейвлетов как инструмента фильтрации проекционных данных и с целью повышения устойчивости алгоритмов реконструкции.

Вейвлеты – это обобщенное название семейств математических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени [6, 14, 2].

Кратномасштабный анализ позволяет анализировать изображение одновременно для разных масштабов. Кратномасштабный анализ определяется следующими свойствами [1, 9, 4, 2]:

рассмотрим цепочку пространств

, они имеют свойства

, где , ;

;

 для ;

и пусть существует , что – ортонормированный базис в , где .

Идея заключается в том, что для любого набора замкнутых подпространств, удовлетворяющих этим условиям, существует ортонормированный базис вейвлетов  для , что для

,  – ортогональное проектирование на .

Другими словами кратномасштабный анализ может описать подпространства, определяемые свойствами, описанными выше, причем . Кроме того, существует , тогда, для  выполняется

,

где  – ортонормированный базис в ,

, .

Функцию  называют “масштабирующей функцией” [4]. Кроме того, существует функция , называемая “вейвлетом, ассоциированным с данным кратномасштабным анализом” [4], для которого . Функция  может быть выражена следующим образом: , где , где черта обозначает комплексное сопряжение.

Тогда получим

Вводим , , тогда

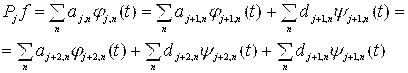                                 (1)

и такое преобразование можно продолжить далее (см. рисунок 1).

Рисунок 1 – Схематичное представление вейвлет–преобразования

 – коэффициенты дискретного вейвлет–преобразования (их еще называют аппроксимирующие и детализирующие коэффициенты вейвлет-преобразования [6]). Соответственно

            (2)

         (3)

Таким образом, в данном случае дискретное вейвлет–преобразование производит перевод последовательности коэффициентов  в последовательности коэффициентов  [21]. Множества ,  позволяют по формулам (1)–(3) численно находить коэффициенты дискретного вейвлет–преобразования.

Применим преобразование (1) к зашумленным проекционным данным параллельной веерной геометрии сканирования , получим следующее представление [2]:

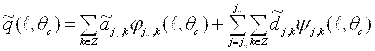,                    (4)

где:

,  – коэффициенты вейвлет–преобразования;

 – масштабирующая функция;

 – вейвлет, ассоциированный с данным кратномасштабным анализом;

с=1,…, M₁ (M₁ – число отсчетов ракурса).

Для веерной геометрии сканирования получим следующее:

,

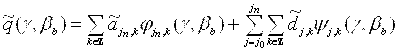где:

b=1,…, M₂ (M₂ – число отсчетов ракурса).

Считается, что шум содержится в высокочастотных компонентах, т. е. находится в коэффициентах вейвлет-преобразования, отвечающих за более малые масштабы (). Фильтрация сводится к обрезанию “высоких частот”, что равносильно приравниванию к нулю коэффициентов  ниже заданного значения (порога). В результате ожидается, что структура обрабатываемых данных, которая лежит в основе сигнала и может быть зашумлена, сохранится и проявится после очищения от шума [8]. Существуют различные примеры задания порогов, например предложенные Donoho и Johnstone в работе [15] и Birge и Massart [10, 11] и их модификации.

Таким образом, алгоритм вейвлет–фильтрации проекционных данных сводится к следующим шагам [2]:

1.  Проведение вейвлет–преобразования проекционных данных. Например, с использованием стационарного дискретного вейвлет–преобразования;

2.  Задание порога для коэффициентов вейвлет–преобразования  в соответствии с их уровнем;

3.  Проведение пороговой обработки;

4.  Восстановление проекционных данных по измененным коэффициентам. Например, с использованием обратного стационарного дискретного вейвлет–преобразования.

Существуют различные типы пороговой обработки [18, 20, 19]. Пусть ,  – вейвлет–коэффициенты некоторого уровня  до фильтрации и после соответственно,  – значение порога, тогда:

мягкая пороговая обработка определяется следующим образом

                            ;

жесткая пороговая обработка

                   ;

аффинная пороговая обработка

закручивающаяся пороговая обработка

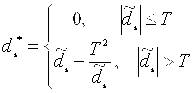
В том числе при сжатии изображений используется равномерное квантование ( – параметр сжатия):

Далее приведен пример этих типов пороговой обработки (см. рисунок 2).

Рисунок 2 – Пример использования различных типов пороговой обработки:

а) без пороговой обработки, б) мягкая пороговая обработка,

в) жесткая пороговая обработка, г) аффинная пороговая обработка,

д) закручивающаяся пороговая обработка,

е) равномерное квантование;

Очевидно, что выбор порога Т играет важную роль. Слишком малое значение порога не может удалить шумовые составляющие, слишком большие значения могут удалить полезные составляющие сигнала [20]. Выбор порога также может быть нескольких типов. Порог может зависеть от уровня вейвлет–коэффициентов или от их пространственной локализации.

·     глобальный порог: значение порога на всех уровнях постоянно, ;

·     адаптирующийся в пространстве порог: изменение значения порога зависит от свойств пространственной локализации каждого вейвлет-коэффициента;

·     порог, зависящий от уровня: для каждого уровня вейвлет-преобразования выбираются различные значения порога.

Некоторые способы поиска порога:

1.  Универсальный порог [15, 13]: , n – число отсчетов сигнала. Этот порог является оптимальным для мягкой вейвлет-фильтрации и случайного гауссовского шума.

2.  Минимаксный порог [18]: ,  – выбирается исходя из минимаксного правила, т. е. , где  – оценка среднеквадратичной ошибки между искомой и найденной функциями.

3.  Штейновская объективная оценка риска [16, 22]: в основе стоит тот же принцип, что и при поиске минимаксного порога, но с различными оценками ошибки.

4.  Штрафной порог [10]: порог устанавливается на основании правила Birge-Massart,  , где , – вейвлет-коэффициенты , отсортированные в порядке убывания своих абсолютных значений, n – число отсчетов сигнала, .

5.  Адаптированный порог: ,  – локальная ошибка исследуемой функции, которая может быть оценена с использованием алгоритма [12].

Как видно при определении всех порогов нужно знать . Наиболее широко используемая оценка была предложена Donoho и Johnstone [17]:

,

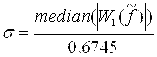где  – нижний уровень детализирующих вейвлет-коэффициентов.

Таким образом, изменяя значения детализирующих коэффициентов , ответственных за высокие частоты, т. е. определяя их “вклад” в высокочастотные составляющие шумов и артефактов, можно провести фильтрацию проекционных данных .

Кроме рассмотренных типов пороговой обработки автором предлагается ввести в рассмотрение обработку, основанную на синтезе жесткой пороговой обработки и равномерного квантования. Ее название «Пороговая обработка с перепадом»:

где    – значение порога,  – параметр сжатия ().

В качестве сравнения двух реконструкций будем использовать количественный анализ характеристик соответствующих функций. Для анализа погрешности были использованы две оценки уровней ошибок реконструкции между изображениями [7]. t_i,j и h_i,j – плотности i-го элиза в j-ой строке матриц для первой и второй реконструкций (матрицы изображений имеют размер ).

         ;                            

err₁ – нормированная абсолютная средняя мера различия, err₂ – средняя квадратичная ошибка реконструкции.

Теорема: Вейвлет–фильтрация проекционных данных для пороговой обработки с перепадом для корректного выбора значения порога и использование метода регуляризации уменьшает или не изменяет нормированную абсолютную среднюю меру различия и среднюю квадратичную ошибку реконструируемого распределения линейных коэффициентов ослабления.

Доказательство: Будем рассматривать веерные проекционные данные, для параллельных проекционных данных доказательство будет аналогичным. Используя (1) можем записать зашумленные проекционные данные в следующем виде:

,

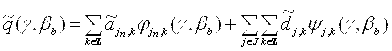где:

b=1,…, M₂ (M₂ – число отсчетов ракурса).

Проекционные данные без шума запишутся следующим образом:

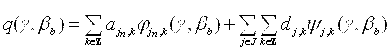
Корректный выбор значения порога означает, что существует множество , зависящее от порогового значения Т и , такое что  для , и существует множество , такое что  для , для которых выполняется

где:

 (N₂ – число отсчетов детектора).

Так как шум содержится в высокочастотных компонентах, т.е. находится в коэффициентах вейвлет-преобразования, отвечающих за более малые масштабы [8, 15], тогда отфильтрованные проекционные данные  (используется вейвлет–фильтрация для пороговой обработки с перепадом) представимы формулой:

,

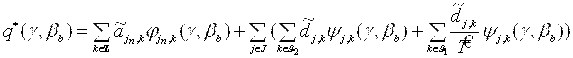где  – параметр сжатия ().

Рассмотрим нормированную абсолютную среднюю меру различия, 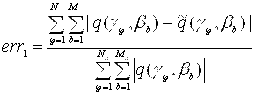, как видно знаменатель постоянен, поэтому достаточно рассмотреть только числитель и только для одного значения , а затем результат обобщить на сумму всех значений.

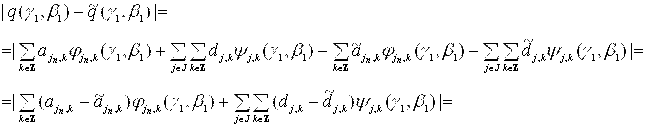
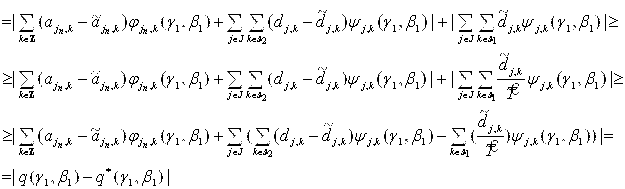
Таким образом, получили

,

т. е. вейвлет-фильтрация для пороговой обработки с перепадом уменьшает или не изменяет нормированную абсолютную среднюю меру различия. Для средней квадратичной ошибки реконструкции и для двумерного вейвлет-преобразования доказательство проводится аналогичным образом.

Если зашумленные проекционные данные приближаются к точным (без шума), относительно среднеквадратичной ошибки, тогда параметр регуляризации можно выбрать таким образом, что регуляризованное решение будет приближаться к точному (41), т. е. из  следует , где  – реконструируемые распределения линейных коэффициентов ослабления для соответствующих проекционных данных.

Но корректность выбора порога играет важную роль. Как было отмечено выше, слишком большие значения могут удалить полезные составляющие сигнала [20]. При проведении вейвлет–фильтрации для пороговой обработки с перепадом для параметра сжатия  всегда можно вернуться к исходной функции, применяя параметр сжатия . В этом заключается главное преимущество данной фильтрации.

На рисунке 3 представлены реконструкции изображений по зашумленным проекционным данным (на идеальные проекционные данные аддитивно накладывался гауссовский шум с ) с использованием различных методов фильтрации.

Рисунок 3 – Реконструкции изображений по зашумленным проекционным данным

Список литературы:

1.Добеши И. Десять лекций по вейвлетам. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 464 с.

2.Лавров С. А., Симонов Е. Н. Реконструкция томографических изображений методом обратного проецирования с использованием вейвлет-фильтрации проекционных данных // Медицинская физика. – 2011. – № 1. – С. 59–68.

3.Петров Ю. П., Сизиков В. С. Корректные, некорректные и промежуточные задачи с приложениями: Учебное пособие для вузов. – СПб: Политехника, 2003. – 261 с.

4.Пикалов В. В., Непомнящий А. В. Итерационный алгоритм с вэйвлет-фильтрацией в задаче двумерной томографии // Вычислительные методы и программирование. – 2003. – Т. 4. – С. 244–253.

5.Симонов Е. Н. Рентгеновская компьютерная томография. Монография. –Снежинск: РФЯЦ-ВНИИТФ, 2002. – 364 с.

6.Смоленцев Н. К. Основы теории вейвлетов. Вейвлеты в Matlab. – М.: LVR Пресс, 2005. – 304 с.

7.Хермен Г. Восстановление изображений по проекциям: Основы реконструктивной томографии. – Пер. с англ. – М.: Мир, 1983 – 352 с.

8.Штарк Г. -Г. Применение вейвлетов для ЦОС. – Пер. с англ. – М.: Техносфера, 2007. – 192 с.

9.Aldroubi A., Unser M. Wavelets in medicine and biology. Boca Raton: CRC Press, 1996.

10.Birge L., Massart P. "From model selection to adaptive estimation," in D. Pollard, Festchrift for L. Le Cam, Springer, 1997, pp. 55–88.

11.Birge L., Massart P. Gaussian model selection. J. Eur. Math. Soc. 3, 2001. – pp. 203–268.

12.Chang S. G., Yu B., Vetterli M. Spatially adaptive wavelet thresholding with context modeling for image denoising. IEEE Transactions on Image Processing, 2000. – Vol. 9, № 9. – pp. 1522–1531.

13.Coifman R., Donoho D. Translation-invariant De-noising. in Wavelets and Statistics, Antoniadis, A. and Oppenheim, G., Eds. New York NY: Springer-Verlag, 1995.

14.Daubechies I. The wavelet transform, time-frequency localization and signal analysis // IEEE Trans. Inform. Theory. – 1990. – Vol. 36. – pp. 961–1005.

15.Donoho D. De-noising by soft-thresholding // IEEE Trans. Inform. Theory. – 1995. – 41, № 3. – pp. 613–627.

16.Donoho D. Nonlinear solution of linear inverse problems by wavelet-vaguelette decompositions // Journal of Applied and Computational Harmonic Analysis, 1995. – Vol. 2, № 2. – pp. 101–126.

17.Donoho D., Johnstone I. Adapting to Unknown Smoothness via Wavelet Shrinkage // Journal of American Statistics Association, 1995. – Vol. 90, № 432. – pp. 1200-1224.

18.Donoho D., Johnstone I. Ideal spatial adaptation via wavelet shrinkage. – Biometrika, 1994. – Vol. 81. – pp. 425–455.

19.Gao H. Wavelet shrinkage denoising using the non-negative garrote // J. Comp. Graph. Statist. – 1998. – Vol. 7. – pp. 469–488.

20.Jin Yinpeng, Angelini E., Laine A. Wavelets in medical image processing: de-noising, segmentation, and registration. – New York. – 2004. – 66 p.

21.Louis A. K., Maass D., Rieder A. Wavelets: theory and applications. – New York: Wiley, 1997. – 342 p.

22.Stein C. Estimation of the mean of a multivariate normal distribution. Annals of Statistics, 1981. – Vol. 9. – pp. 1135–1151.