СКОРОСТЬ СХОДИМОСТИ ПРИБЛИЖЕННЫХ МЕТОДОВ РАСЧЕТА НЕСТАЦИОНАРНОГО ДВИЖЕНИЯ ЖИДКОСТИ НАД ТВЕРДЫМ ТЕЛОМ

Ерунова Ирина Борисовна

канд. физ.-мат. наук, доцент, Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург

E-mail: 

В работе исследуется математическая модель фазового перехода между твердым телом и жидкостью с движущейся свободной границей раздела сред.

Оценки скорости сходимости приближенного решения стацио­нарной задачи о движении жидкости над твердым телом были получены в [3, с. 4]. Разрешимость полной системы уравнений Навье-Стокса и Стефана была доказана в [2, с. 26]. Существование единственного приближенного решения полной системы термодина­мических уравнений, уравнений движения жидкости и границы раздела фаз в нестационарном случае рассматривалось в [1, с. 89]. В настоящей работе получены оценки скорости сходимости единствен­ного приближенного решения нестационарной системы уравнений Навье-Стокса и Стефана к точному решению следующей задачи.

Пусть твердое тело и жидкость с коэффициентами теплопроводности  и , коэффициентами удельной теплоемкости  и  соответственно занимают в пространстве область

Область  ограничена снизу границей

и сверху

.

Граница раздела сред Г не пересекается с  и . Твердое тело с плотностью  расположено в области , ограниченной снизу , а сверху Г. Жидкость с плотностью  и динамической вязкостью  занимает область , ограниченную снизу Г, а сверху .

Задача состоит в приближенном определении температуры , скорости движения жидкости , давления жидкости , перемещения  свободной границы Г в направлении нормали , удовлетворяющих начальным и граничным условиям

                                                               (1)

                                 (2)

                                            (3)

                                                                                        (4)

здесь:  — удельная теплота плавления. Область  может быть продолжена в направлении осей  и  с периодами и  соответственно. Предполагается, что  периодические функции по переменным  и  с периодами и .

Рассмотрим этапы решения задачи (1)—(4). Пусть Т время плавления, выберем натуральное число , обозначим шаг по времени  а моменты по времени   Процесс начинается с начальных условий (4)

начальная граница  известна. Предположим, существует единственное приближенное решение  в момент времени . Задача состоит в определении нового приближенного решения в момент времени

Температура  является решением линейной задачи фиксированной области

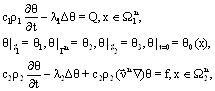                            (5)

с известными

Следующая задача состоит в определении приближенных  и , удовлетворяющих нестационарной системе уравнений Навье-Стокса в ,

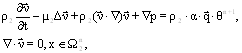                   (6)

с заданными  

Наконец, новое приближенное перемещение  границы  получается из уравнений

                                       (7)

В анализе нестационарных задач (5)—(7) используется разностная схема Кренка-Николсона для переменной по времени. На каждом шаге итераций приближенные решения предлагаемых вариационных формулировок задач (5) и (6) получаются методом конечного элемента. Рассмотрим непрерывные функции

Основным результатом работы является следующая теорема.

Теорема. Пусть

Если существует точное решение задачи (1)—(4)

тогда задача (1)—(4) имеет единственное приближенное решение

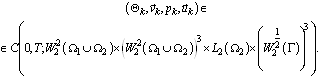
Если для точного решения задачи (1)—(4) выполняются дополнительные условия

тогда существует положительное число  такое, что для любого  справедливы неравенства

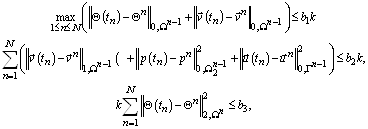
где постоянные ,  и  не зависят от .

Список литературы:

1. Ерунова И. Б. Об оценках скорости сходимости приближенного решения задачи об испарении жидкости // Сборник трудов III Всероссийская научно-практическая конференция «Актуальные проблемы управления информационными системами ». 2009. — СПб. С. 87—91.
2. Ерунова И. Б., Ривкинд В. Я.. Исследование задачи об испарении жидкости // Вестник Ленингр. университета. 1991. вып. 2, № 8. С. 22—27.
3. Erunova I., Neittaanmaki P. Convergence estimates for approximation of the steady flow liquid and gas over a solid. Report 18. 1997. —Jyvaskyla: University of Jyvaskyla. 15 p.