РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ВЫСОКИХ СТЕПЕНЕЙ НА БАЗЕ КОМПЬЮТЕРНОЙ ДИАКОПТИКИ

Бакимжанов Бауыржан

студент 2 курса, кафедра ВТИС КГУ им.Коркыт Ата, г. Кызылорда

Е-mail: mehanika_15@mail.ru

Тайышева Зере Адилбеккызы

студентка 1 курса, кафедра ВТИС КГУ им.Коркыт Ата, г. Кызылорда

Сейтмуратов Ангысын

научный руководитель, д.ф.-м.н, ассоц.профессор КГУ, г. Кызылорда

Из электротехники известно, что расчет переходных процессов электрических цепей связан с решением дифференциальных уравнений и одной из сложных моментов решения их в операторной форме является – решение характеристического уравнения, описывающего гармонический состав.

Так для цепочки в N ячеек:

Характеристическое уравнение принимает вид:

A_nXⁿ  + A_n-1X^n-1 + A_n-2X^n-2 +  …. A₁X + A₀ = 0;                                            (1)

Точное решение подобных полиномов представляет большую трудность без специальных компьютерных программ, а полиномы выше третьего порядка не имеют точного решения.

Ниже покажем, что для определенного класса алгебраических полиномов существует простой способ решения.

При составлении характеристического полинома пятого порядка мы получили уравнение:

 X⁵+0,275X⁴ +11,01X³ +1,15X² +3,27X +0,0313 = 0;                                    (2)

Замечаем, что график из коэффициентов при X имеет вид некого хребта, как будет доказано ниже, достаточно точное решение этого класса уравнение можно проводить простым разбиением его на три части:

 X²+0,275X +11,01 = 0;                                                                                  (3)

 X₁= -0,1375+i 3,31;

X₂= -0,1375 - i 3,31;

11,01X² +1,15X +3,27 = 0;                                                                            (4)

X₃= -0,0,0521+i 0,54;

X₄= -0,0,0521-i 0,54; 

3,27X +0,0313 = 0;                                                                                        (5)

X₅= - 0,00957;

Точные решения:

X₁= -0,087+i 3,27;  X₂= -0,087-i 3,27; 

X₃= -0,047 + i 0,55;  X₄= -0,047 - i 0,55;

X₅= - 0,00996;

Замечаем, что приближенные значения корней   отличаются от истинных всего на 2 – 3 %

Данный способ решения алгебраических полиномов будем называть – диакоптикой алгебраических уравнений некоторого класс характеристических уравнений электрических цепей.[2,с. 45][5,с. 90]

Докажем и покажем на примерах, что внешним признаком разложения полиномов является то, что начальные и конечные коэффициенты  полиномом должны быть меньше средних, а это в свою очередь обязывает постепенное уменьшение модулей корней полиномов.[4,с 31-32]

Так для полинома: P⁴+aP³+bP²+cP+d=0 по теореме Виета имеем

a=X₁+X₂+X₃+X₄ ;

b=X₁X₂+X₁X₃+X₁X₄+X₂X₃+X₃X₄+X₂X₄ ;

c=X₁ X₂X₃+X₁X₂X₄+X₂X₃X₄+X₁X₃X₄ ;

d=X₁X₂X₃X₄ ;

Если Х₁<X₂<=X₃>X₄  нетрудно вычислить, что в этом случае между коэффициентами будет следующая зависимость: a<b<=c>d

Для проверки найденного критерия эффективного разложения полиномов была составлена программа на языке Borland Pascal Version 7.0 [1,с 288],[3]

Ниже приведен пример, в которых вначале задаются корни уравнения пятой степени, далее по теореме Виета находятся коэффициенты многочлена, записывается уравнение, вычисляются приближенные значения корней простым разбиением на части и далее рассчитывается погрешность вычисленных корней с истинными значениями.

Пример №1

Введем переменные х многочлена 5-ой степени

-3        x 1= -3

30       x 2= 30

200     x 3= 200

40       x 4= 40

-3        x 5= -3

Уравнение имеет вид:х5-2688x4+7520x3+20158x2+13589x1+2160000=0

В результате решения:

x1=-1.590E+02        погрешность1= 5.198E+01%

x2=-6.741E-01         погрешность2= 1.022E+00%

x3=-2.681E+00        погрешность3= 1.013E+00%

x4= 2.798E+00         погрешность4= 9.301E-01%

x5= 2.688E+03         погрешность5= 0.000E+00%

Как нетрудно заметить, погрешность расчетов составляет несколько процентов, что зачастую достаточно в инженерных расчетов, а при необходимости провести уточнение по известным методам.

Ниже показана рисунок по методу расчета основных параметров и моделирования  геометрических составляющих (биссектрисы, медианы, радиусы, описывающие и вписывающие окружности и т.д.) и по трем сторонам рассчитываются, масштабируется и строятся основные геометрические линии

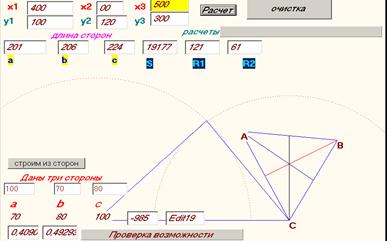
Рисунок 1- Расчет основных параметров и моделирования  геометрических составляющих

В случае неправильной постановки задачи об этом дается сообщение и предоставляется возможность нового ввода параметров.

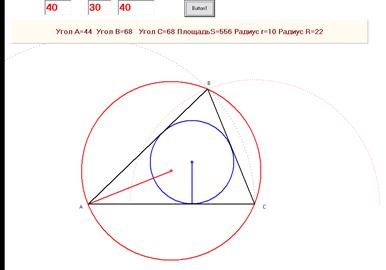
Рисунок 2- Расчет  по трем сторонам основной геометрической линии

При моделировании статических объектов следует в цикле сохранять постоянные интервалы между повторяющимися элементами.

Исходя из вышеизложенного, в работе были рассмотрены основные теоретические принципы создания математических и физических моделей статически и динамических программ, для решения алгебраических полиномов высоких степеней.

Моделирование физических процессов позволяет с заданной точностью рассчитать необходимые параметры процесса, наглядно иллюстрировать динамический и статический ход физического явления.

Проведенные исследования могут быть использованы для решения широких задач в области математики и физике, позволят активизировать познавательную активности в обучении  средний и высшей школе.

Список литературы:

1. Баженова И.Ю. Языки программирования-М.:Диалог-МИФИ,1997 - 288 с.
2. Дмитришин Р.В., Шаповалов Ю.И. Диакоптический алгоритм анализа сложных линейных цепей на ЭВМ // Автоматизация проектирования в электронике.– Киев, 1975.– Вып. 12.– С. 42–46.
3. Миллер Т., Пауэл Д. Использование Delphi 7. Специальное издание. К.: Диалектика, 1997.
4. Сейтмуратов А.Ж. Метод декомпозиции в тории колебания двухслойной пластинки в строительных конструкциях// Научно-технический и производственный журнал ПГС .-2006.-№3.-С.31-32
5. Dumitriu L., Iordach M., Mandache L. Diakoptic modified nodal method for symbolic analysis of analog circuits // SMACD–2002.– Sinaia, 2002.– P. 89–94.