ОБРАБОТКА  ЦИФРОВЫХ  СИГНАЛОВ  В  ЭЛЕКТРОЭНЕРГЕТИКЕ

Сикорский  Сергей  Петрович

E-mail: 

Ковалев  Глеб  Александрович

E-mail: 

Ляхнов  Денис  Валерьевич

студенты  3  курса,  кафедра  электроснабжения  промышленных  предприятий  ОмГТУ, 
РФ,  г.  Омск

E-mail:  denis95.16@mail.ru

Осипов  Дмитрий  Сергеевич

научный  руководитель,  канд.  техн.  наук,  доцент  ОмГТУ, 
РФ,  г.  Омск

Цифровая  обработка  сигналов  заключается  в  том,  что  напряжение,  ток,  или  любой  другой  физический  сигнал  преобразовываются  в  последовательность  чисел,  которая  способна  подвергаться  математическим  преобразованиям  в  вычислительном  устройстве.  Трансформированный  цифровой  сигнал,  т.  е.  эту  числовую  последовательность  при  необходимости  можно  преобразовать  обратно  в  напряжение  или  ток.

Первоначальный  сигнал,  предположим  напряжение,  является  непрерывной  зависимостью  от  времени.  Подобный  сигнал,  определенный  в  каждый  момент  времени,  называют  аналоговым  (analog).  А  представляющая  этот  сигнал  последовательность  чисел,  в  данной  обработке,  называется  дискретным  рядом  (discreteseries).  Аналоговому  сигналу  она  не  может  соответствовать  точно.  Числа,  которые  составляют  последовательность,  представляют  собой  значения  сигнала  в  отдельные  (дискретные)  моменты  времени  и  называются  отсчетами  сигнала  (samples).  Они,  как  правило,  берутся  через  одинаковые  промежутки  времени  T,  которые  называются  периодами  дискретизации.  Величина  обратная  периоду  дискретизации  –  частота  дискретизации:.  Круговая  частота,  соответствующая  ей  определяется  следующим  образом:  .

Преобразование  в  последовательность  от  счетов  аналогового  сигнала  называется  дискретизацией  (sampling),  результатом  этого  преобразования  называют  дискретным  сигналом  [1,  с.  127–128].

При  вычислении  комплексных  амплитуд  гармоник  сигнала  используется  формула,  представляющая  линейную  комбинацию  его  отсчетов. 

При  работе  с  данными  дискретными  последовательностями  зачастую  оперируют  номерами  отсчетов  и  спектральных  гармоник  сигналов  не  привязывая  их  к  действительному  масштабу  частоты  и  времени.  Такое  выражение  сигнала  называется  дискретным  преобразованием  Фурье:

        (1)

Также  существует  дискретное  преобразование,  обратное  Фурье,  которое  переходит  к  временным  отсчетам  от  дискретного  спектра.  Оно  выражается  следующей  формулой:

        (2)

Данное  выражение  отличается  от  прямого  ДПФ  (1)  знаком  в  показателе  комплексной  экспоненты,  а  также  перед  оператором  суммирования  наличием  множителя  1/N  [1,  c.  608].

Растекание  спектра

В  анализируемом  сигнале  последовательность  отсчетов  будет  являться  периодически  продолженной  во  времени  как  вперед,  так  и  назад.  При  этом  следует  отметить:  если  значения  конечных  и  начальных  отсчетов  сигнала  будут  достаточно  сильно  различаться,  при  периодическом  повторении  на  стыках  сегментов  возникают  скачки,  из-за  которых  спектр  сигнала  расширяется.

Это  явление,  называемое  растеканием  спектра(spectrumleakage),  можно  нагляд­но  проиллюстрировать  на  простейшем  примере  вычисления  спектра  дискретно­го  гармонического  сигнала

(3)

Если  анализируемая  последовательность  содержит  целое  число  периодов  гармо­нического  сигнала  (то  есть  если  отношение  NωT/(2π)  является  целым  числом),  то  периодически  продолженный  сигнал  представляет  собой  гармонические  коле­бания  (без  скачков),  а  подстановка  (3)  в  формулу  ДПФ  (1)  показывает,  что  вычисленное  ДПФ  содержит  лишь  два  спектральных  отсчета,  отличных  от  нуля:

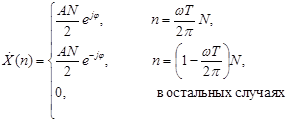(4)

Таким  образом,  подобно  спектру  непрерывного  гармонического  сигнала,  ДПФ  отличается  от  нуля  только  для  двух  значенийn.  Однако  если  отношение  NωT/(2π)  не  является  целым  числом,  спектр  становится  значительно  более  богатым.  Это  имеет  простое  объяснение:  в  данном  случае,  когда  отношение  NωT/(2π)  не  равно  целому  числу,  периодически  продолженная  последовательность  уже  не  будет  являться  набором  отсчетов  непрерывной  синусоиды.  Вследствие  этого,  в  полном  соответствии  со  свойствами  преобразования  Фурье,  в  спектре  появятся  дополнительные  составляющие.

В  качестве  примера  показано,  что  сигнал  происходит  в  виде  суммы  трех  синусоид  (50,  250,  350  Гц).

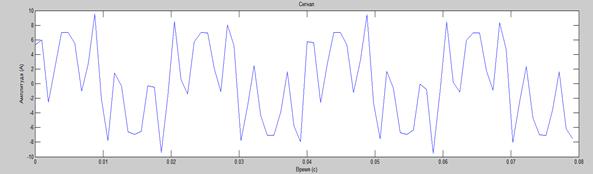
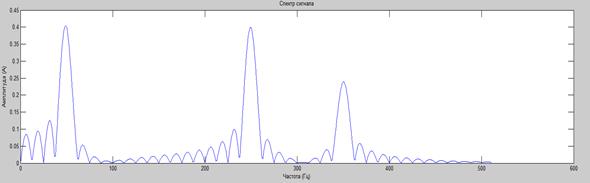
Рисунок  1.  Растекание  спектра

Из  рисунка  видно,  что  при  вычислении  ДПФ  появляются  дополнительные  составляющие  в  спектральном  составе.  Это  явление  называют  растеканием  спектра.

Эффект  растекания  спектра  наблюдается  в  том  случае,  если  хотя  бы  для  одной  из  дискретных  гармоник,  входящих  в  спектральный  состав  последовательности,  с  частотой  f_iна  интервале  NT  укладывается  нецелое  число  периодов  T_iи  отношение:

(3)

оказывается  не  целым  числом,  а  частота  гармоники  f_i­–  не  кратной  периоду  дискретизации  по  частоте:

Вследствие  этого  в  периодическом  продолжении  гармоники  с  частотой  f_iпоявятся  разрывы  (скачки)  на  границах  периода  последовательности,  из-за  которых  спектр  расширяется.

Для  уменьшения  эффекта  растекания  спектра  (полностью  он  принципиально  неустраним)  применяют  весовые  функции  (окна)  –  вещественные  неотрицательные  последовательности,  максимальные  в  центре  и  монотонно  спадающие  к  границам,  что  ослабляет  влияние  разрывов  при  периодическом  продолжении  последовательности  [2,  c.  166–167].

Фурье  –  преобразование  нестационарных  сигналов

На  практике  сигнал  тока  является  случайной  величиной.  Пример:  жилой  массив.  В  каждой  квартире  постоянно  включаются  или  отключаются,  причём  в  разное  время,  отдельные  электроприёмники.  Рассмотрим  нестационарный  сигнал  и  проведем  для  него  преобразование  Фурье.

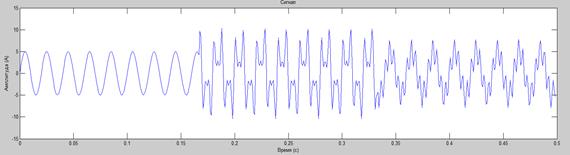
Рисунок  2.  Фурье  преобразование  нестационарного  сигнала

Сравнивая  рисунки  1  и  2  делаем  вывод:  преобразование  Фурье  не  учитывает  время  появления  гармоник.  Т.  е.  преобразование  Фурье  дает  информацию  о  частотах,  но  не  сообщает,  когда  они  присутствуют.

Полученная  характеристика  содержит  похожие  три  пика,  как  и  ранее,  создастся  впечатление,  что  все  три  частоты  в  сигнале  присутствуют  на  всем  рассматриваемом  интервале.  Это  есть  главный  недостаток  преобразования  Фурье  –  преобразование  дает  информацию  о  частотах,  но  не  сообщает,  когда  они  присутствуют.  Сигналы  разные,  но  преобразование  Фурье  дает  похожий  результат  без  указания  времени  появления  гармоник.

Список  литературы:

1. Сергиенко  А.Б.  Цифровая  обработка  сигналов.  //  А.Б.  Сергиенко  –  СПб.:  Питер,  –  2002.  –  608  с.
2. Солоника  А.И.  Цифровая  обработка  сигналов  и  MATLAB:  учеб.  пособие  //  А.И.  Солонина,  Д.М.  Клионский,  Т.В.  Меркучева,  С.Н  Петров.  –  СПб.:  БХВ–  Петербург,  –  2013.  –  512  с.:  ил.  –  (Учебная  литература  для  вузов).