Статья опубликована в рамках: XXXVII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 24 декабря 2015 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
E-mail:
Сибирякова Валентина Александровна
научный руководитель, старший преподаватель, ФПМК, каф. программирования, ТГУ,
РФ, г. Томск
Задача коммивояжёра – важная задача транспортной логистики, отрасли, занимающейся планированием транспортных перевозок. Задача состоит в определении кратчайшего гамильтонова цикла в графе – отыскании наилучшего маршрута, и является одной из самых интересных, практически значимых и одновременно сложных задач оптимизации. Выделяют два типа решения этой задачи: точные и эвристические [1].
Широко распространенным точным не переборным алгоритмом решения задачи коммивояжера является метод ветвей и границ [2]. Суть метода – в направленном частичном переборе допустимых решений с отсевом подмножеств, заведомо не содержащих оптимальных решений. То есть вычисляется нижняя оценка стоимости всех маршрутов, затем на каждом шаге в результате анализа матрицы стоимости определяется дуга (ветвь), которая добавляет к этой стоимости минимальное значение из всех возможных.
Одним из эвристических методов искусственного интеллекта является муравьиный алгоритм Марко Дориго. Этот алгоритм имитирует передвижение колонии муравьев в природе [6].
Направление движения муравья определяет случайное число, которое отправляет его из i в город j с большей вероятностью, если функция Pi,j(t) примет наибольшее значение. Вероятность перехода высчитывается по формуле (1):
|
|
|
где: τi,j – феромон между этими городами,
di,j(-1) – видимость города,
α и β – коэффициенты, регулирующие решение. Если α = 0, то алгоритм становиться жадный и выбор основывается только на расстоянии между городами, если β = 0, то выбор города базируется на значении феромона [8].
Феромоны – это некоторое вещество, которое «откладывают» муравьи, помечая пройденный маршрут между городами. Количество ферамона для муравья с номером k, проходящему по ребру (i,j), будет вычисляться по формуле (2):
|
|
|
где: Tk(t) – маршрут, пройденный муравьём k,
Lk(t) – цена текущего решения для k-ого муравья,
Q – параметр, имеющий значение порядка цены оптимального решения [8].
Дополнительная модификация алгоритма заключается во введении «элитных» муравьёв. Их основное назначение – усиление лучших маршрутов за счет выделения большего количества феромонов, которое вычисляется по формуле (3).
|
|
|
где: L* – длина наилучшего текущего маршрута,
Q – параметр, имеющий значение порядка цены оптимального решения.
В такой системе количество элитных муравьёв является дополнительным параметром, требующим определения. Ибо, для слишком большого числа элитных муравьев алгоритм может «застрять» на локальных экстремумах.
Феромоны, как и в природе, испаряются. Скорость испарения зависит от параметра, который, требует отдельного рассмотрения. Если значение скорости будет слишком велико, решение быстро выродится.
Генетический алгоритм – это эвристический метод поиска с использованием механизмов, напоминающих биологическую эволюцию [4].
Суть метода в том, чтобы представить маршрут в виде цепочки генов – хромосомы, с которой могут происходить все возможные биологические изменения – мутация, кроссинговер и скрещивание.
Дадим несколько определений, модифицированных для нашей задачи.
Мутация – это преобразование хромосомы, случайно изменяющее одну или несколько позиций генов. В нашем случае, два случайно выбранных гена будут меняться местами.
Кроссинговер (так же кроссовер или скрещивание) – это операция, при которой из двух хромосом порождается одна или несколько новых. В простейшем случае кроссинговер в генетическом алгоритме реализуется так же, как и в биологии, но с небольшой модификацией, так как маршрут не должен проходить через 1 город дважды [5]. Хромосомы разрезаются в случайной точке и обмениваются частями без повторений, с дальнейшим сдвигом и добавлением недостающих генов. Например, (1, 2, 3, 4, 5) и (2, 1, 4, 3, 5) разрезаем между третьим и четвертым генами и обмениваем их части, сдвигая повторяющиеся гены. Получаются потомки: (1, 2, 3, 5, 4) и (2, 1, 4, 5, 3).
Селекция – это выбор определенной доли популяции, которая останется «в живых» на данном этапе эволюции. Селекция необходима, так как множество потомков и мутантов имеют сниженную жизнеспособность и отсеиваются в процессе естественного отбора.
«Эволюционный процесс» продолжается несколько жизненных циклов (поколений). Критерием остановки может быть: нахождение глобального решения; исчерпание числа поколений, отпущенных на эволюцию; исчерпание отпущенного на эволюцию времени [3; 4].
Схема интегрированного поиска
Основная идея интегрированного поиска – объединение алгоритмов в многоуровневую модель, в зависимости от требований к решению [7].
На первом предварительном этапе будут генерироваться одно или несколько множеств, для получения первоначальной популяции решений. В данном блоке возможно использование «быстрых» алгоритмов.
Далее получаем семейство решений с помощью генетического алгоритма. Главная цель этого уровня – быстро получить удовлетворительное решение, не заботясь о том, что оно может «застрять» на локальных экстремумах. Эти решения оцениваются и подаются на вход в роевые алгоритмы.
Затем, на последнем этапе, выбираем наиболее приемлемый подход для решения задачи: ММК – модифицированный алгоритм муравьиной колонии или РИ – алгоритм на основе роевого интеллекта; Эти алгоритмы позволяют «вышибить» решение из локального экстремума.
Оцениваем эффективности полученного решения. При удовлетворительном результате окончательный вариант выдается пользователю (заказчику). Иначе происходит изменение управляющих параметров, и процесс повторяется либо до достижения критерия останова, либо до получения приемлемого решения.
Теоретическая временная сложность работы интегрированной системы составляет: О(N(1+N)), что незначительно превышает время работы роевых алгоритмов, но интегрированный метод обладает повышенной точностью.
Выводы
В данной работе сформулировано решение одной из основных проблем XXI века – транспортной проблемы.
Для решения поставленной задачи автор предлагает использование интегрированного подхода к нахождению оптимальных решений для задач транспортного типа с использованием методов, инспирированных природными системами.
Данные методы имеют значительные преимущества относительно стандартных методов решения. Они способны быстро адаптироваться к изменениям, варьировать точность в зависимости от требований и выдавать решение, приближенное к точному, за минимальное время. Это позволит создавать системы, использующие данный метод, и не требующие больших трудозатрат. Следовательно, расчеты можно будет производить как большим компаниям для огромного количества единиц автотранспорта, так и обычным пользователям с любого гаджета, для просчета единичных случаев.
Список литературы:
- Беспалько В.П. Образование и обучение с помощью компьютеров / В.П. Беспалько. – М. : Высш. шк., 1998. – 135 с.
- Борознов В.О. Дополнение метода ветвей и границ для решения задачи коммивояжера // Вестн. Ростов. гос. ун-та путей собщения. – 2007. – № 1. – С. 160–163.
- Борознов В.О. Исследования генетических методов решения задачи коммивояжёра / В.О. Борознов, О.Г. Ведерникова // Вестн. Ростов. гос. ун-та путей собщения. – 2004. – № 1. – С. 42–45.
- Гладков Л.А., Курейчик В.М., Курейчик В. В. Генетические алгоритмы / Л.А. Гладков. – Ростов-н/Д.: ООО «Ростиздат», 2004 г.
- Курейчик В.В. Эволюционные методы решения оптимизационных задач. Таганрог, 1999, ТРТУ.
- МакКоннелл Дж. Основы современных алгоритмов // Дж. МакКоннелл. – М.: Техносфера, 2004. – 368 с.
- Романовский И.В. Алгоритмы решения экстремальных задач / И.В. Романовский. – М.: Наука, 1977. – 352 с.
- Dorigo M., Maniezzo V., Colorni A. The Ant System: Optimization by a colony of cooperating objects // IEEE Trans. on Systems, Man, and Cybernetics. – 1996. – Part B.
дипломов


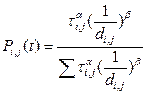
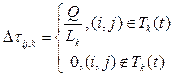
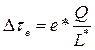
Оставить комментарий