Статья опубликована в рамках: XXXVI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 24 ноября 2015 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Сборник статей конференции
дипломов
ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ НАВЬЕ-СТОКСА В ПЕРЕМЕННЫХ «ВИХРЬ-ФУНКЦИЯ ТОКА»
Качалкина Яна Николаевна
магистр 1 курса, кафедра вычислительной техники СПбГЭТУ (ЛЭТИ),
РФ, г. Санкт-Петербург
E-mail: kachalkina_yana@mail.ru
Орлова Наталья Сергеевна
научный руководитель, канд. техн. наук, младший научный сотрудник, ученый секретарь Совета молодых ученых ЮМИ ВНЦ РАН,
РФ, г. Владикавказ
В настоящее время моделирование гидродинамических процессов является популярной задачей.
Основными уравнениями, описывающими плоское течение несжимаемой вязкой жидкости с постоянными свойствами при отсутствии внешних сил, являются два уравнения количества движения (уравнения Навье-Стокса) и уравнение неразрывности. Для решения двумерных уравнений Навье-Стокса наиболее популярным является подход с использованием переменных «вихрь-функция тока» [3]. Одной из трудоемких частей решения уравнений является итерационный процесс получения стационарного решения, физический смысл, которого заключается в выполнении итераций до тех пор, пока решение не будет зависеть от времени. Такой подход называется методом установления [2].
Рассмотрим задачу о ламинарном течении вязкой несжимаемой жидкости в каверне (рис. 1). Каверна квадратная, стороны равны L. Высота входного и выходного отверстия равны d. Стенки Г1, Г2, Г3, Г4 – неподвижные и непроницаемые; Г5, Г6 – входная и выходная границы соответственно. Распределение скорости u на входной границе направлено вдоль оси x по параболическому закону (закону Пуазейля). В выходном сечении распределение такое же, как на входной границе.
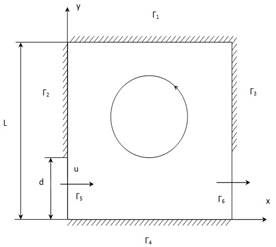
Рисунок 1. Схема каверны
Для численного решения предпочтительнее форма записи уравнения Навье-Стокса в переменных «вихрь – функция тока»:
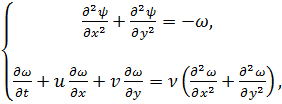 (4)
(4)
где: ![]() – вихрь;
– вихрь;
![]() – функция тока;
– функция тока;
![]() – вертикальная скорость;
– вертикальная скорость;
![]() – горизонтальная скорость;
– горизонтальная скорость;
![]() – кинематический коэффициент вязкости;
– кинематический коэффициент вязкости;
Начальные условия:
· в каверне: ![]() (5)
(5)
· между входным и выходным отверстиями:
![]() (6)
(6)
![]() (7)
(7)
где
![]() (8)
(8)
где: ![]() – начальный профиль скорости;
– начальный профиль скорости;
![]() ,
, ![]() – параметры параболического уравнения;
– параметры параболического уравнения;
![]() – высота входного отверстия;
– высота входного отверстия;
Граничные условия:
На стенках Г1, Г2, Г3:
![]() (9)
(9)
На стенках Г4, Г5, Г6:
![]() (10)
(10)
На стенках Г1, Г2, Г3, Г4:
![]() (11)
(11)
На стенках Г5, Г6:
![]() (12)
(12)
Для вычисления ![]() на стенках Г5 и Г6 были добавлены фиктивные слои, где значение
на стенках Г5 и Г6 были добавлены фиктивные слои, где значение ![]() принималось равным значению
принималось равным значению ![]() на границе.
на границе.
Расчетную область покрываем равномерной сеткой. Каждое дифференциальное уравнение в частных производных заменяется системой алгебраических уравнений, число которых равно числу внутренних узлов сетки.
Для нахождения поля скоростей в следующий момент времени, необходимо найти поле вихря и поле функции тока. Сначала определяется вихрь:
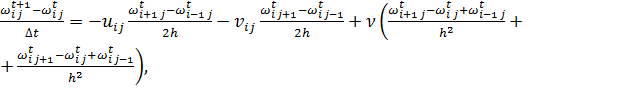 (13)
(13)
где ![]() (14)
(14)
![]() (15)
(15)
Затем, на основе полученных ![]() , методом итераций получаем
, методом итераций получаем ![]()
![]() (17)
(17)
Рассчитываются новые граничные значения ![]() с использованием ранее полученных
с использованием ранее полученных ![]() и
и ![]() во внутренних точках.
во внутренних точках.
На твердых стенках Г1, Г2, Г3, Г4:
![]() (18)
(18)
На твердых стенках Г5, Г6:
![]() (19)
(19)
Затем, снова перечитываются ![]() и
и ![]() до тех пор, пока задача не выйдет на стационарное решение с заданной точностью.
до тех пор, пока задача не выйдет на стационарное решение с заданной точностью.
С помощью разностной схемы получены результаты численного решения стационарной задачи, при заданном числе Рейнольдса.
На рисунке 2 показаны линии стационарного поля течения внутри каверны при числе Рейнольдса равным 150 и 100.
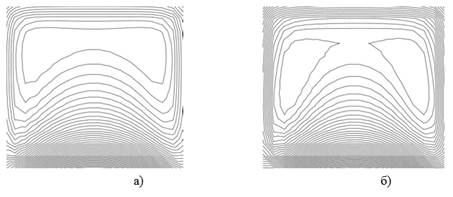
Рисунок 2. Линии тока стационарного решения а) Re = 150; б) Re=100
Видно, что течение имеет циркуляционный характер. Наибольшая интенсивность расположения линий тока находится в нижней части, где находятся входное и выходное отверстия. При меньших значениях числа Рейнольдса вихрь разрывается в центре на два симметричных вихря (рис. 2. б).
Рассмотрим графики горизонтальной и вертикальной составляющих скорости в центре каверны при Re = 100 (рис. 3.).
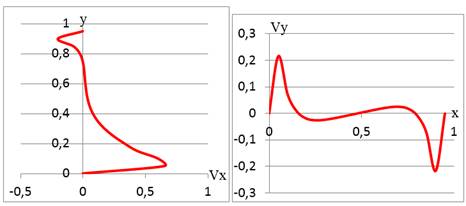
Рисунок 3. Горизонтальная и вертикальная составляющие скорости
Такие перепады скоростей образуются из-за двух, формирующихся внутри каверны, вихрей. Оба вихря движутся против часовой стрелки.
Заключение.
С помощью метода конечных разностей построена конечно-разностная схема, аппроксимирующая систему уравнений Навье-Стокса в переменных «вихрь-функция тока». Полученные разностные уравнения решаются методом установления (итерации).
Написана программа, моделирующая движение жидкости в каверне с начальными и граничными условиями. Графически были представлены и проанализированы линии тока установившегося решения для различных чисел Рейнольдса и графики горизонтальной и вертикальной составляющих скорости. При большом числе узлов сетки вычисление занимает продолжительное время, решением данной проблемы является распараллеливание алгоритма вычислений.
Список литературы:
- Иванов В.Г. Численное решение уравнений Навье-Стокса в переменных «функция тока-вихрь», Национальный исследовательский Томский государственный университет, Томск, 2012, стр. 1–3.
- Каменецкий Е.С. Решение уравнений в частных производных методом конечных разностей // Математический анализ и математическое моделирование: тр. междун. конф. молодых учен. Владикавказ, 2010 г., стр. 27–35.
- Роуч П. Вычислительная гидродинамика. Москва: Мир, 1980 г., стр. 618.
- Chow W.K., Gao P.Z. Large Eddy Simulation of Turbulent Convective Cavity Flow, International Journal of Computational Fluid Dynamics, – 2004, – Vol. 18 (8), – pp. 641–650.
дипломов


Оставить комментарий