МОДЕЛИРОВАНИЕ  ДВУХФАЗНОЙ  СИСТЕМЫ  МАССОВОГО  ОБСЛУЖИВАНИЯ

Черанёв  Александр  Александрович

студент  3  курса,  кафедра  радиоэлектронных  и  телекоммуникационных  систем  ИРИТ-РТФ  УрФУ,  РФ,  г.  Екатеринбург

Е-mail:  kraxc @yandex.ru

Самусевич  Галина  Александровна

научный  руководитель,  доцент,  канд.  тех.  наук,  ИРИТ-РТФ  УрФУ,  РФ,  г.  Екатеринбург

Представляется  стохастическая  модель  двухканальной  системы  массового  обслуживания  (СМО)  с  ограничениями  на  время  пребывания  заявки,  как  в  очереди,  так  и  в  системе.  Один  поток  входных  заявок.  Поток  входных  заявок  и  оба  потока  обслуживания  являются  простейшими.  Имеется  возможность  задать  наибольшее  число  входных  приоритетных  заявок  и,  следовательно,  время  работы  модели,  что  позволяет  изучать  эффективность  рассматриваемой  системы,  как  в  ходе  переходного  процесса,  так  и  в  установившем  режиме  ее  работы.

Разрабатываемый  программный  продукт  предназначен  для  создания  двух  лабораторных  работ: 

1.  лабораторная  работа  для  студентов  бакалавриата  для  изучения  влияния  относительного  приоритета  на  эффективность  СМО.  Дисциплина  —  «Основы  теории  массового  обслуживания».

2.  лабораторная  работа  для  студентов  магистратуры  предполагает  изучение  принципов  моделирования  стохастических  динамических  процессов.  Дисциплина  —  «Методы  моделирования  и  оптимизации».

Программный  продукт  будет  разработан  на  языке  C++  с  использованием  алгоритмов  для  решения  поставленной  задачи  и  получения  необходимых  данных.  В  итоге,  будет  смоделирована  двухканальная  система  массового  обслуживания  с  ограничениями  на  время  пребывания  заявки,  как  в  очереди,  так  и  в  системе. 

Описание  переменных

M   —  число  входных  заявок  (j[1,  M]);

t_j   =  t_j-1  +  η  —  момент  времени  появления  в  системе  j-ой  заявки,

где  η  =  1/λ  —  среднее  значение  интервала  времени  между  соседними  заявками,  λ  —  параметр  показательного  закона  распределения  вероятностей  случайной  величины  ;

  —  время  ожидания  в  очереди  j-ой  заявкой  освобождения  i-го  канала;

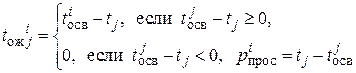
  —  момент  времени  освобождения  i-го  канала,  i  =  1,  2,

где  μ_i  –  средняя  величина  времени  обслуживания  заявки  i-ым  каналом.  показательный  закон  распределения  вероятностей,  определяющая  длительность  обслуживания  j-ой  заявки  i-ым  каналом;

  —  время  пребывания  j-ой  заявки  в  системе;

  —  наибольшее  время  пребывания  заявки  в  очереди;

  —  наибольшее  время  пребывания  заявки  в  системе.

Текущие  показатели  эффективности  системы

b   —  суммарное  число  обслуженных  заявок  к  моменту  времени  t_j;

c   —  число  заявок,  покинувших  систему  необслуженными  из-за  ограничения  на  время  пребывания  в  очереди  к  моменту  времени  t_j;

d   —  число  заявок,  покинувших  систему  необслуженными  из-за  ограничения  на  время  их  пребывания  в  системе  к  моменту  времени  t_j;

—  суммарное  время  обслуживания  заявки  i-м  каналом;

  —  суммарное  время  простоя  i-го  канала;

  —  суммарное  время  пребывания  заявок  в  очереди  к  моменту  времени  t_j;

  —  суммарное  время  пребывания  заявок  в  системе  к  моменту  времени  t_j.

Результирующие  показатели  эффективности  системы

Результирующие  показатели  эффективности,  вычисляются  после  окончания  цикла  по  j  (когда  j  =  M)  для  момента  времени  .

  –—  вероятность  обслуживания;

  —  вероятность  отказов,  вызванных  ограничением  на  время  пребывания  заявки  в  очереди  и  на  время  пребывания  заявки  в  системе;

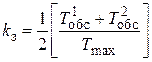  —  коэффициент  загрузки  системы;

  —  коэффициент  простоя  системы;

  —  суммарное  время  пребывания  заявок  в  очереди. 

  —  суммарное  время  пребывания  заявок  в  системе.

Приложение

Результаты  моделирования

Таблица  1.

Таблица  2.

Макет  разрабатываемой  программы

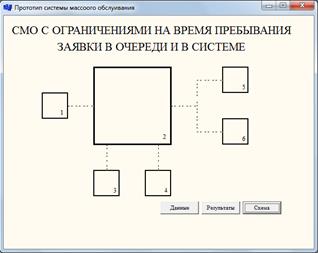
Рисунок  1.  Главное  окно  со  структурной  схемой  СМО  с  ограничениями.  (1  —  входящий  поток,  2  —  очередь,  3  —  Количество  отказов  из-за  превышения  времени  пребывания  в  очереди,  4  —  отказ  из-за  превышения  времени  пребывания  заявки  в  системе,  5,6  —  каналы  обслуживания)

Рисунок  2.  Окно  ввода  данных

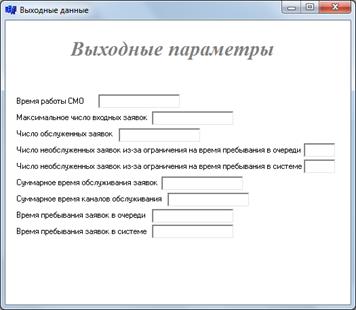
Рисунок  3.  Выходные  параметры

Список  литературы:

1.Моделирование  систем:  Учебник  для  студентов  высш.  Учеб.  заведений/[С.И.  Дворецкий,  Ю.А.  Муромцев,  В.А.  Погодин,  А.Г.  Схиртладзе].  М.:  Изд.  Центр  «Академия»,  2009.  —  320  с.

2.Советов  Б.Я.,  Яковлев  С.А.  С56  Моделирование  систем:  Учебник  для  вузов  3-е  изд.,  перераб.  и  доп.  М.:  Высш.шк.,  2001.  —  343  с.:  ил.  (УДК  519.87,  ББК  22.18,  С56).

3.Самусевич  Г.А.  Основы  теории  массового  обслуживания:  Конспект  лекций  /  Г.А.  Самусевич.  Екатеринбург:  Изд-во  ГОУ  ВПО  -  УГТУ  УПИ,  2005.  —  102  с.