Статья опубликована в рамках: XXXII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 мая 2015 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРИМЕНЕНИЕ МЕТОДОВ ТЕОРИИ ГРАФОВ ПРИ ОЦЕНКЕ ЭФФЕКТИВНОСТИ БИЗНЕС-ПРОЦЕССОВ
Петрова Марина Александровна
студент 2 курса магистратуры, кафедра УИТЭС ВлГУ им. А.Г. и Н.Г. Столетовых, РФ, г. Владимир
Е-mail : pma-33@yandex.ru
Шутов Антон Владимирович
научный руководитель, канд. физ.-мат. наук, доцент кафедры УИТЭС
ВлГУ им. А.Г. и Н.Г. Столетовых, РФ, г. Владимир
В теории графов существует огромное множество видов задач, которые можно использовать при оценке эффективности бизнес-процессов и их сравнения. В нашем случае разберем задачу нахождения пути максимальной эффективности.
Допустим, что задан определенный граф, в котором для каждой дуги (i; j) указаны два числа ![]() которые можно определить как эффект при выполнении конкретной операции —
которые можно определить как эффект при выполнении конкретной операции — ![]() и затраты на эту операцию —
и затраты на эту операцию — ![]() . Эффективность
. Эффективность ![]() пути
пути ![]() определяется как отношение его эффекта
определяется как отношение его эффекта ![]() к затратам
к затратам ![]() , то есть
, то есть ![]() Сама задача подразумевает поиск пути
Сама задача подразумевает поиск пути ![]() * максимальной эффективности:
* максимальной эффективности: ![]()
Допустим, что решение ![]() поставленной задачи уже известно, то по факту
поставленной задачи уже известно, то по факту ![]() в данном случае выполнено:
в данном случае выполнено:
![]()
![]() (1)
(1)
Соответственно, задача сводится к поиску минимального значения ![]() , для которого выполняется (1). Иначе говоря, необходимо выполнить поиск минимального
, для которого выполняется (1). Иначе говоря, необходимо выполнить поиск минимального ![]() , такого, чтобы все пути (длина которых равна
, такого, чтобы все пути (длина которых равна![]() ) в графе имели неположительную длину (неравенство (1) должно быть соблюдено также и для пути максимальной длины).
) в графе имели неположительную длину (неравенство (1) должно быть соблюдено также и для пути максимальной длины).
Алгоритм решения:
1. Допустим, что ![]() . Ищем путь m1 максимальной длины. Допускаем, что
. Ищем путь m1 максимальной длины. Допускаем, что ![]() (при
(при ![]() длина пути
длина пути ![]() равна нулю).
равна нулю).
2. Найдем максимальный путь ![]() при
при ![]() . Если длина пути
. Если длина пути ![]() , обозначаемая как
, обозначаемая как ![]() , равна нулю, то рассматриваемая задача уже решена. Если
, равна нулю, то рассматриваемая задача уже решена. Если ![]() , то считаем
, то считаем ![]() и отсюда можно найти максимальный путь
и отсюда можно найти максимальный путь ![]() при
при ![]() и т. д.
и т. д.
Далее необходимо рассмотреть путь максимальной эффективности с учетом штрафов. Допустим, что для каждой дуги ![]() — вершинного графа задаются два показателя: эффект
— вершинного графа задаются два показателя: эффект ![]() и время
и время ![]() . Каждый путь
. Каждый путь ![]() из начальной вершины в конечную вершину определяет некоторый процесс. Продолжительность пути в данном случае — это сумма времен его дуг. Если длительность (продолжительность) рассматриваемого процесса отлична от заданного изначально времени T, то налагаются штрафы
из начальной вершины в конечную вершину определяет некоторый процесс. Продолжительность пути в данном случае — это сумма времен его дуг. Если длительность (продолжительность) рассматриваемого процесса отлична от заданного изначально времени T, то налагаются штрафы ![]() , которые пропорциональны отклонению, т. е.:
, которые пропорциональны отклонению, т. е.:
![]()
где коэффициенты a и b могут быть и отрицательными, и положительными.
В конечном итоге задача подразумевает, что необходимо найти путь m*, который представляет собой максимизацию разности между эффектом и штрафами, т. е.:
![]()
Определим, что ![]() , где l — некоторый параметр,
, где l — некоторый параметр, ![]() — длительность (продолжительность) наиболее оптимального пути при параметре l, т. е. пути, который имеет максимальную длину, при этом подразумевая, что длина измеряется в
— длительность (продолжительность) наиболее оптимального пути при параметре l, т. е. пути, который имеет максимальную длину, при этом подразумевая, что длина измеряется в ![]() [1] .
[1] .
Из рассмотренного видно, что при увеличении l величина ![]() не возрастает. Определим
не возрастает. Определим ![]() и
и ![]() как длительности (продолжительности) наиболее оптимального пути при условии, что l равна a и, соответственно, b;
как длительности (продолжительности) наиболее оптимального пути при условии, что l равна a и, соответственно, b; ![]() — сами пути (для того, чтобы их найти, нужно решить 2 задачи, каждая из которых задача на поиск пути максимальной длины). Рассмотрим 6 случаев (первоначальную задачу можно разделить на 2 подзадачи — поиска максимума
— сами пути (для того, чтобы их найти, нужно решить 2 задачи, каждая из которых задача на поиск пути максимальной длины). Рассмотрим 6 случаев (первоначальную задачу можно разделить на 2 подзадачи — поиска максимума ![]() при
при ![]() и при
и при ![]() ).
).
Допустим, что ![]() в этом случае
в этом случае ![]() и:
и:
1. если ![]() , то
, то ![]() — оптимальное решение;
— оптимальное решение;
2. если ![]() , то
, то ![]() — оптимальное решение;
— оптимальное решение;
3. если ![]() , то, при сравнении по длинам
, то, при сравнении по длинам ![]() и
и ![]()
![]() , выбирать необходимо именно путь максимальной длины.
, выбирать необходимо именно путь максимальной длины.
Допустим, что ![]() тогда в этом случае
тогда в этом случае ![]() и:
и:
4. если ![]() , то
, то ![]() — оптимальное решение;
— оптимальное решение;
5. если ![]() , то
, то ![]() — оптимальное решение;
— оптимальное решение;
6. если ![]() , то данная задача вообще не имеет рациональных методов решения.
, то данная задача вообще не имеет рациональных методов решения.
Для обеспечения возможности применения данного алгоритма для задачи оценки эффективности бизнес-процессов (БП) нужно найти отображение множества БП в множество элементов графа [1].
Ориентированный граф включает три множества: множество вершин (V), множество дуг графа (Е) и множество весов графа (L).
Бизнес-процесс можно описать следующими множествами: множество участников бизнес-процесса (S), множество документов, сообщений, файлов (D), множество трудоемкостей выполнения функций бизнес-процесса (ТО), множество функций бизнес-процесса (O).
В данном случае возможны различные варианты отображения. Рассмотрим только некоторые из них.
1. D®V, S®Е — данное отображение определяет состояния БП и участников БП на каждом этапе обработки информации.
Рассмотрим пример.
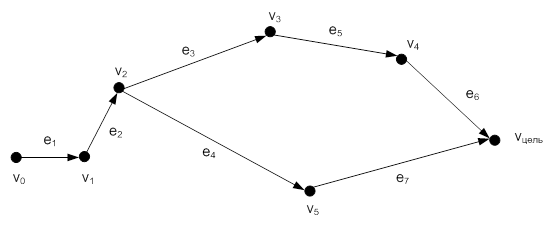
Рисунок 1 – Граф отображения D→V, S→Е
Таблица 1.
Множество E — множество участников БП (Пример)
|
Обозначения |
Описание |
|
e1 |
Консультант |
|
e2 |
Сметчик |
|
e3 |
Старший специалист отдела водных коммуникаций |
|
e4 |
Старший специалист отдела систем освещения |
|
e5 |
Специалист отдела водных коммуникаций |
|
e6 |
Специалист отдела систем освещения |
|
e7 |
Специалист отдела согласования |
Таблица 2.
Множество V — элементов множество документов, сообщений, файлов
|
Обозначения |
Описание |
|
V0 |
Заказ клиента |
|
v1 |
Техническое задание |
|
v2 |
Смета проекта |
|
v3 |
План-график выполнения проекта водных коммуникаций |
|
v4 |
Проект водных коммуникаций |
|
v5 |
План-график выполнения проекта системы освещения |
|
Vцель |
Проектная документация для клиента |
2. D®V, О®Е — данное отображение показывает состояния БД и функций БП. Рассмотрим пример.

Рисунок 2. Граф отображения D→V, О→Е
Таблица 3.
Множество E — множество функций БП
|
Обозначения |
Описание |
|
e1 |
Подготовка ТЗ исходя из заказа клиента |
|
e2 |
Расчет сметы проекта |
|
e3 |
Разработка план-графика подготовки проекта водных коммуникаций |
|
e4 |
Разработка план-графика подготовки проекта системы освещения |
|
e5 |
Подготовки проекта водных коммуникаций |
|
e6 |
Согласование проекта с водоканалом |
|
e7 |
Подготовки проекта системы освещения |
Таблица 4.
Множество V — множество документов, сообщений, файлов
|
Обозначения |
Описание |
|
V0 |
Заказ клиента |
|
v1 |
Техническое задание |
|
v2 |
Смета проекта |
|
v3 |
План-график выполнения проекта водных коммуникаций |
|
v4 |
Проект водных коммуникаций |
|
v5 |
План-график выполнения проекта системы освещения |
|
Vцель |
Проектная документация для клиента |
3. D®V, О®Е, Т®L — данное отображение показывает состояния БП и функций БП, а также трудоемкость их выполнения. Рассмотрим пример.
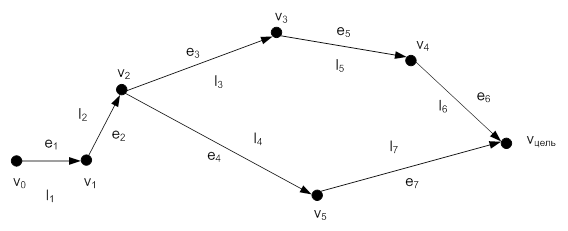
Рисунок 3. Граф отображения D→V, О→Е, Т→L
Таблица 5.
Множество E — множество функций БП
|
Обозначения |
Описание |
|
e1 |
Подготовка ТЗ исходя из заказа клиента |
|
e2 |
Расчет сметы проекта |
|
e3 |
Разработка план-графика подготовки проекта водных коммуникаций |
|
e4 |
Разработка план-графика подготовки проекта системы освещения |
|
e5 |
Подготовки проекта водных коммуникаций |
|
e6 |
Согласование проекта с водоканалом |
|
e7 |
Подготовки проекта системы освещения |
Таблица 6.
Множество V — множество документов, сообщений, файлов
|
Обозначения |
Описание |
|
V0 |
Заказ клиента |
|
v1 |
Техническое задание |
|
v2 |
Смета проекта |
|
v3 |
План-график выполнения проекта водных коммуникаций |
|
v4 |
Проект водных коммуникаций |
|
v5 |
План-график выполнения проекта системы освещения |
|
Vцель |
Проектная документация для клиента |
Таблица 7.
Множество L — множество трудоемкостей выполнения функций БП
|
Обозначения |
Описание |
|
l0 |
8 чел/часов |
|
l1 |
10 чел/часов |
|
l2 |
6 чел/часов |
|
l3 |
8 чел/часов |
|
l4 |
8 чел/часов |
|
l5 |
56 чел/часов |
|
L7 |
48 чел/часов |
|
L6 |
24 чел/часов |
Рассмотренные нами примеры представляют собой отдельные бизнес-процессы. С помощью графов можно строить модели разных уровней детализации — от элементарной функции до целого этапа обработки информации.
Список литературы:
1.Альпин Ю.А., Ильин С.Н. Дискретная математика: графы и автоматы. Учебное пособие. Казань: Казанский государственный университет им. В.И. Ульянова-Ленина, 2006. — 78 с
2.Cardoso J., «How to measure the control-flow complexity of web processes and workflows» in The Workflow Handbook, pp. 199—212, 2005.
3.Rol´on E., Ruiz F., Garc´ıa F., and Piattini M., «Towards a suite of metrics for business process models in BPMN» in 8th International Conference on Enterprise Information Systems, Paphos, Cyprus, 2006.
дипломов


Оставить комментарий