Статья опубликована в рамках: XXXII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 мая 2015 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
МЕТОДЫ ОБРАБОТКИ И СЖАТИЯ АУДИОСИГНАЛА С ПОМОЩЬЮ ВЕЙВЛЕТ АНАЛИЗА И БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Кондыбаева Алмагуль Бауржановна
студент 3 курса, кафедра инженерной кибернетики, НИТУ МИСиС, РФ, г. Москва
Е-mail : almakonde18@gmail.com
Шихеева Валерия Владимировна
научный руководитель, доцент. физ.-мат. наук, доцент НИТУ МИСиС, РФ, г. Москва
Введение
В данной работе рассматриваются методы обработки аудио сигналов. Целью данного исследования является поиск и исследование методов обработки сигналов.
Главной целью работы является изучение методов представления звука в цифровой системе. Это можно трактовать так, что это изучение возможностей математики получать звук таким образом, чтобы уничтожить искажения, недостатки качества, шумы, помехи и т. д., т. е. получение звука наиболее приближенному естественному живому настоящему звучанию, получение качественного, красивого звука.
Существует множество способов очистки от шумов, множество способов представления звука (окрас отдельных инструментов, работа с тембром), наложение отдельных эффектов реверберации и прочих различных трансформаций звука. И для того, чтобы поподробнее изучить вопрос методов и возможностей обработки звука исследуются этапы поиска, выбора подходящего базиса, отвечающий определенным критериям и требованиям, а также подбор подходящих преобразований. Также очень сильно накладывается требование быстродействия алгоритмов обработки. Это обеспечит повсеместное использование алгоритмов преобразований звука.
В данной работе описывается работа с аудио сигналом и представление его в цифровой системе, а также попытка, с помощью ряда экспериментов найти новые базисы наилучшим образом отвечающим решению обработки аудио сигнала.
Список сокращений:
1. АЦП — аналогово-цифровой преобразователь (analogue-to-digital converter as known as ADC)
2. ЦАП — Цифро-аналоговый преобразователь (digital-to analogue converter, DAC)
3. НЧ фильтры — низкочастотные фильтры
4. ВЧ фильтры — высокочастотные фильтры
5. ДПФ, DFT — Дискретное преобразование Фурье
6. БПФ, FFT — Быстрое преобразование Фурье
Сигнал. Дискретные и непрерывные сигналы.
Сигнал — зависимость одной величины от другой (функция).
С нашей точки зрения «сигнал» будет трактоваться как функция. Наша функция может трактоваться, как функция на интервале вещественных чисел R (непрерывный или аналоговый сигнал) или трактоваться, как функция на конечном множестве точек или как функция на бесконечном дискретном множестве точек (например Z дискретный или цифровой сигнал).
Дискретные и непрерывные аудио сигналы на множестве ![]() .
.
Большинство реальных звуковых сигналов являются непрерывными функциями (здесь мы пренебрегаем квантовыми эффектами).
Для обработки и работы с сигналом требуется перевести его в дискретную цифровую форму. Для этого как один из способов применяется равномерное по времени измерение значения сигнала на определенном промежутке времени и вводить полученные значения амплитуд в виде цифровой информации на компьютер. Измерения нужно делать часто, для того чтобы по полученному дискретному сигналу можно было бы восстановить исходный непрерывный аналоговый сигнал.
Такой процесс замеров сигналов и перевод в цифровой формат называется процессом дискретизации [2, с. 6].
Многие устройства проводят дискретизацию. Например, звуковая карта дискретизирует сигнал с микрофона. В результате таких операций (дискретизации) непрерывный (аналоговый) сигнал переводится в цифровой (дискретный).
Устройство, которое производит замеры аналогового сигнала называется аналогово-цифровым преобразователем (АЦП, analogue-to-digital converter as known as ADC) [2, с. 14].
Частота, с которой АЦП производит замеры называется частотой дискретизации [2, с. 12].
Важный вопрос:
С какой точностью можно восстановить исходный сигнал по его дискретным значениям и какие необходимы условия, действующие на частоту и исходный сигнал?
Читатель наверняка знаком с тем, что любую непрерывную функцию можно представить в виде ряда Фурье, разложенном на некотором отрезке.
Смысл разложения представляется в том, чтобы представить функцию в виде периодического ряда синусоид с различными амплитудами и фазами с кратными частотами. Амплитуды (коэффициенты) при синусоидах называются спектром функции.
Говорят, что сигнал имеет ограниченный спектр, если после определённого номера, все коэффициенты спектра равны 0.
Важное применение находит фундаментальная теорема Котельникова. Ответ мы ищем применяя ее.
Теорема 1.1 Котельникова-Найквиста-Шеннона (или теорема отсчетов):
Если аналоговый сигнал имеет конечный (финитный), ограниченный по ширине спектр, то он может быть однозначно без потерь восстановлен по своим замерам, взятыми с частотой, большей или равной удвоенной верхней частоте: ![]()
Тогда исходный аналоговый сигнал x(t) можно точно восстановить из его цифровых отсчетов x(nT), пользуясь интерполяционной формулой
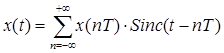
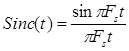
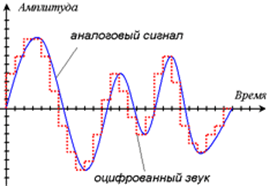
Рисунок .1 Оцифрованный звук
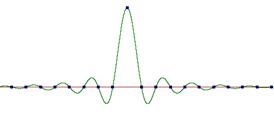
Рисунок 2. Бесконечно затухающие колебания
Устройство, которое интерполирует дискретный сигнал до непрерывного, называется цифрово-аналоговым преобразователем (ЦАП, digital-to analogue converter, DAC) [2, с. 15].
Например, в проигрывателях компакт-дисков для восстановления звука по цифровому звуковому сигналу, записанному на компакт-диск.
Наложение спектров (алиасинг)
Если попытаться оцифровать сигнал с недостаточной для него частотой дискретизации (или если спектр неограничен) по полученной цифровой выборке нельзя будет восстановить сигнал. Восстановленный сигнал будет выглядеть таким образом, как если бы, частоты лежащие выше половины частоты дискретизации, отразились от половины частоты дискретизации и перешли в нижнюю часть спектра.
Например, мы попытались оцифровать музыку, спектр которой лежит внутри частоты 20000 Гц, но при записи один из электроприборов сгенерировал помеху (например, дисплей) с ультразвуковой частотой в 40000 Гц, которая проникла в наш аналоговый звуковой сигнал. Мы производим оцифровку с частотой в 41000 Гц, при этом мы рассчитываем по т. Котельникова, что звук ниже 41000/2 Гц будет записан, верно. Но! Так как помеха лежит выше этой частоты, возникнет алиасинг. Потом помеха отразится в нижнею часть спектра на частоту около 5000 Гц. Затем мы пытаемся восстановить сигнал и пропускаем через ЦАП и слышим помеху на частоте 5000 Гц. Это шум. Таким образом помеха из неслышимой части ультразвуковой части переместилась в слышимую и появился шум на записи.
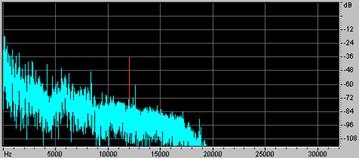
Рисунок 3 Помеха отразилась от половины частоты дискретизации в нижнюю часть спектра и наложилась на звук. Помеха переместилась в слышимый диапазон
Алиасинг.(на рисунке 3)
Как можно его избежать?
Существует 2 способа:
Использовать более высокую частоту дискретизации. Чтобы весть спектр уместился ниже половины частоты дискретизации
Второй способ: искусственно ограничить спектр сигнала перед оцифровкой.
Существуют устройства, называемые фильтрами для изменения спектра сигнала. Например, фильтры низких частот (НЧ- фильтры, low-pass filters), которые пропускают, не изменяя все частоты ниже заданной, и удаляет все частоты выше заданной.
Такие частоты называются частотами среза (cutoff frequency filters) фильтра.
Одно из важных применений НЧ фильтров является искусственное ограничение спектра сигнала перед оцифровкой. В этом случае фильтры называются анти-алиасинговыми. Так как они предотвращают возникновение алиасинга при оцифровке сигнала. Часто среза обычно равняется половине частоте дискретизации.
Импульсная Характеристика. Линейность. Инвариантность относительно сдвига .
Мы рассматриваем дискретные линейные системы. На вход подается последовательность чисел x[n] (дискретный сигнал). И на выходе получается последовательность числе y[n]. Как и для непрерывных систем свойства линейности формулируем также.
Для того, чтобы рассмотреть каким образом линейная система может преобразовать входной сигнал в выходной рассмотрим реакцию системы на цифровую дельта-функцию (функция Кронекера). Получаем сигнал вида ![]() =
=![]() т.е. короткий единичный импульс.
т.е. короткий единичный импульс.
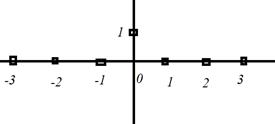
Рисунок 4. Цифровая дельта функция (на рисунке)
Очевидно, что любой дискретный сигнал можно разложить в сумму таких функций, сдвинутых по времени. Например, бесконечный сигнал x[n] можно представить в виде x[n] ![]() .
.
Здесь дельта-функция — это базисные функции. x[i]-коэффициенты в линейной комбинации.
Далее, существует еще одно предположение, которое разумно наложить на нашу систему: в идеальном случае преобразователи должны быть линейными.
Линейность.
1. T(u + v)=T(u)+T(v);
2. T(![]() )=
)=![]() T(u);
T(u);
Линейность-это разумное предположение, которое мы накладываем на нашу математическую модель системы.
Во-первых: эффект действия системы на два сигнала должен быть суммой эффектов действия на каждый из сигналов в отдельности. Во-вторых, если мы умножаем входную систему на некоторую величину, то и входной сигнал должен быть умножен на нее.
Инвариантность относительно сдвига.
Еще одно предположение для системы — это инвариантность. Это означает, что в различные моменты времени если мы задерживаем сигнал на некоторое время, то единственным эффектом на выходе будет задержка сигнала на то же время. Такое предположение называется инвариантным во времени или инвариантным относительно сдвига.
Введем оператор сдвига: ![]()
Инвариантность относительно сдвига представляем в виде:
T(![]() )=
)=![]() ;
;
Наиболее важным фактом, связанным с базисом Фурье F, является тот факт, что все линейные преобразования, инвариантные относительно сдвига диагонализируются базисом Фурье.
Лемма 1.1. Линейные преобразования, инвариантные относительно сдвига ![]() , все диагонолизируются фактически одним базисом, более того, он ортогональный [1, с. 231].
, все диагонолизируются фактически одним базисом, более того, он ортогональный [1, с. 231].
Теорема 1.2.Пусть T: ![]() линейное преобразование, инвариантное относительно сдвига. Тогда каждый элемент базиса Фурье F является собственным вектором преобразования T. Где T — диагонализируемое преобразование [1, с. 235].
линейное преобразование, инвариантное относительно сдвига. Тогда каждый элемент базиса Фурье F является собственным вектором преобразования T. Где T — диагонализируемое преобразование [1, с. 235].
Доказательство:
Зафиксируем m ![]()
![]()
Пусть ![]() -есть элемент базиса Фурье.
-есть элемент базиса Фурье.
Тогда существуют комплексные скаляры такие, что
![]() (1.0)
(1.0)
Для всех n потому, что F есть базис в ![]() .
.
Применим действия оператора сдвига на единицу:
(![]() )(n)=
)(n)=![]() ; (1.1)
; (1.1)
![]() , то из линейности следует, что:
, то из линейности следует, что:
T(![]() )(n)=
)(n)=![]() ;
;
С другой стороны из равенства (1.1) вытекает также, что
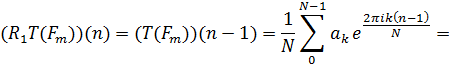
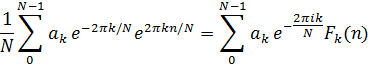
Но для всех n по предположению T есть преобразование, инвариантное относительно сдвига. Сравнивая полученные выше выражения для этих 2 величин и используя единственность разложения вектора по элементам базиса, получаем, что для каждого k=0,1,…,N-1 справедливо равенство:
![]() =
=![]() (1.2)
(1.2)
Если k![]() m , то
m , то ![]() , так как 0
, так как 0![]() .
.
Поэтому равенство 1.2 может выполняться, если только ![]() .
.
Следовательно, мы доказали, что ![]() , только когда k
, только когда k![]() m. Поэтому в равенстве 1.0 все слагаемые пропадают, за исключением членов с номерами k
m. Поэтому в равенстве 1.0 все слагаемые пропадают, за исключением членов с номерами k![]() m, получается
m, получается
![]()
Следовательно, ![]() есть собственный вектор преобразования T с собственным значением
есть собственный вектор преобразования T с собственным значением ![]()
Так как m выбрано произвольно, это показывает, что каждый элемент базиса Фурье есть собственный вектор преобразования Т \. Отсюда следует, что Т диагонализируемо.
Сформулируем еще одну очень важную теорему:
Теорема 1.3 Пусть T: ![]() -
-![]() есть линейное преобразовании. Тогда следующие утверждения верны:
есть линейное преобразовании. Тогда следующие утверждения верны:
1. Т есть преобразование инвариантное относительно сдвига.
2. Матрица ![]() представляющая Т в стандартном базисе Е, есть циркулянтная матрица.
представляющая Т в стандартном базисе Е, есть циркулянтная матрица.
3. Т есть оператор свертки
4. Т есть мультипликаторный оператор Фурье.
5. Матрица ![]() , представялющая Т в базисе Фурье F, есть диагональная матрица.
, представялющая Т в базисе Фурье F, есть диагональная матрица.
Утверждение о диагональной матрице (утв. 5) другими словами сформированное утверждение о том, что Т диагонализируется базисом Фурье.
Стратегия доказательств этой теоремы состоит в последовательном доказательстве 1->2->3->1,3<->4 & 4<->5.
Заметим, что теорема дает и обратную ей теорему, которая утверждает, что линейное преобразование, которое диагонализируется базисом Фурье, есть преобразование инвариантное относительно сдвига.
Индексы для матриц будут изменятся от 0 до N-1 так же, как и в обозначении векторов, т.е. записываем матрицу А размера n![]() как
как
![]()
Мы также распространим соглашение о периодичности для наших матрице, которое мы установили для наших векторов.
Дискретное преобразование Фурье
Представим векторы, которые мы рассматриваем в пространстве ![]() , т. е. последовательности N комплексных чисел. Сейчас мы введем несколько обозначений: сначала пронумеруем эти N чисел индексами j
, т. е. последовательности N комплексных чисел. Сейчас мы введем несколько обозначений: сначала пронумеруем эти N чисел индексами j ![]()
![]() и вместо записи компонент вектора z в виде
и вместо записи компонент вектора z в виде ![]() мы будем записывать их, как z(j). Это определяет новую точку зрения: мы рассматриваем z как функцию, определённую на конечном множестве.
мы будем записывать их, как z(j). Это определяет новую точку зрения: мы рассматриваем z как функцию, определённую на конечном множестве.
![]()
(и это соответствует формальному определению Последовательности, Как функции на множестве индексов)
Вектор в ![]() можно считать функцией, заданной в N точках, следовательно сигналом. Физически мы можем представить себе звуковой сигнал, например музыкальный фрагмент.
можно считать функцией, заданной в N точках, следовательно сигналом. Физически мы можем представить себе звуковой сигнал, например музыкальный фрагмент.
Система — это нечто, преобразующее входной сигнал в выходной. С нашей точки зрения система — это преобразование.
Z вектор столбец

Примем ![]() вместо
вместо ![]() для того, чтобы рассматривать функции для бесконемерного случая и применять в нашей работе.
для того, чтобы рассматривать функции для бесконемерного случая и применять в нашей работе.
![]()
С обычным покомпонентным сложением и скалярным умножением ![]() . Поэтому
. Поэтому ![]() есть N-мерное векторное пространство над полем С. Где одним из стандартных базисов является эвклидов базис E=
есть N-мерное векторное пространство над полем С. Где одним из стандартных базисов является эвклидов базис E=![]() .
.
Здесь ![]() , j=n,
, j=n, ![]() если n
если n![]() .
.
В этом обозначении комплексное скалярное произведение в ![]() определяется так:
определяется так: ![]()
C нормой:![]()
Мы сохраняем понятие ортогональности при условии равенства нулю: ![]()
z![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Также вектор z должен быть периодическим с периодом N:
z (j+N)=z(j) ![]()
Представим ![]() ,
,![]() ,
,![]() ,….,
,….,![]()
![]()
![]()
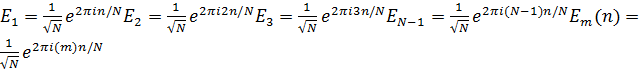
В ![]() воспользуемся Леммой 1.3: Множество
воспользуемся Леммой 1.3: Множество ![]() ,
,![]() ,
,![]() ,….,
,….,![]() есть ортонормированный базис пространства
есть ортонормированный базис пространства ![]() . (М.Фрейзер, 1999)
. (М.Фрейзер, 1999)
Доказательство: Пусть j,k ![]()
![]() =
=![]() =
=
![]() =
=![]() =
=![]()
Если j=k , то все члены внутри группы в последней сумме равны 1.

Следовательно, норма тождественно равна единице.
![]()
Для каждого j. Т. е. все ![]() имеют норму 1.
имеют норму 1.
Так как –N<=j-k<=N
Поэтому сумма есть частичная сумма геометрической прогрессии и
![]() =
=![]()
Сократив степени N при правых слагаемых:
![]() =
=![]() =1
=1
j-k есть целое число, поэтому для каждых j k не равных друг другу выполняется :
![]()
![]() =0
=0
Таким образом, мы получаем ортонормированные элементы ![]()
Поэтому ![]() есть ортонормированное множество. Следовательно мы получили ортогональное множество векторов
есть ортонормированное множество. Следовательно мы получили ортогональное множество векторов ![]() в непрерывном пространстве
в непрерывном пространстве ![]() , где определено комплексное скалярное произведение . и пользуясь Леммой 1.3 наше множество Линейно Независимое множество.
, где определено комплексное скалярное произведение . и пользуясь Леммой 1.3 наше множество Линейно Независимое множество.
Лемма 1.4: Пусть V — пространство с комплексным скалярным произведением, а B — ортогональное множество векторов в этом пространстве и 0 не принадлежит этому множеству. Тогда В есть линейно независимое множество.
Поэтому множество ![]() есть базис пространства
есть базис пространства ![]() .
.
Определение 1.1. Пусть z = ![]()
![]()
![]() / Для m=0,1,….,N-1 определим
/ Для m=0,1,….,N-1 определим
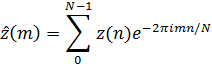
Пусть
![]()
Отображение ![]() в
в ![]() , котрое связывает z и
, котрое связывает z и ![]() называется Дискретным Преобразованием Фурье (ДПФ для него обычно используется аббревиатура DFT).
называется Дискретным Преобразованием Фурье (ДПФ для него обычно используется аббревиатура DFT).
Спектральный анализ.
Часто ДПФ применяется для наблюдения и анализа спектра сигнала. При этом обычно наиболее интересными являются лишь амплитуд ![]() отдельных гармоник, а не их фазы. В этом случае спектр обычно отображается в виде графика зависимости амплитуды от частоты.
отдельных гармоник, а не их фазы. В этом случае спектр обычно отображается в виде графика зависимости амплитуды от частоты.
Перед вычислением спектра сигнала нужно выбрать отрезок сигнала, на котором будет вычисляться спектр. Длина отрезка должна быть степенью двойки (для работы БПФ). Иначе сигнал надо дополнить нулями до нужной длины. После этого к выбранному участку сигнала применяют БПФ. Коэффициенты амплитуд считают по формуле ДПФ. При вычислении спектра указанным образом возможен следующий нежелательный эффект. При разложении функции в ряд Фурье мы полагаем, что функция периодическая, с периодом, равным размеру БПФ. Вычисляется спектр именно такой функции (а не той, из которой мы извлекли кусок). При этом на границах периодов такая функция наверняка будет иметь разрывы (ведь исходная функция не была периодической). А разрывы в функции сильно отражаются на ее спектре, искажая его. Для устранения этого эффекта применяются так называемые взвешивающие окна. Они плавно сводят на нет функцию вблизи краев анализируемого участка. Выбранный для анализа участок сигнала домножается на весовое окно, которое устраняет разрывы функции при «зацикливании» данного участка сигнала. Зацикливание происходит при ДПФ, так как алгоритм полагает, что ДПФ периодическая.
Свертка.
Свертка — основной процесс в цифровой обработке звуков (сигналов). Поэтому важно уметь эффективно ее вычислять. Прямое вычисление свертки требует N*M умножений.
N — длина исходного сигнала,
M — длина ядра свертки.
Часто длина ядра свертки достигает несколько тысяч точек, и число умножений становится огромным.
Теорема Свертки 1.4. Свертка во временной области эквивалентна умножению частотных областей. Свертка в частотной области эквивалентна умножению во временной области [2, с. 15].
Это очень важная теорема, которая позволяет нам понять, что возможна свертка двух сигналов, для этого необходимо перевести сигналы в частотную область, умножит спектры сигналов в частотной области, а затем перевести их обратно во временную область.
Часто возникает потребность произвести сверку очень длинного сигнала, не помещающегося в памяти компьютера, тогда применяется так называемая секвенционная свертка.
Суть ее в том, что длинный сигнал разбивается на более короткие части и каждая эта часть сворачивается с ядром отдельно.
Фильтрация.
Эффект от умножения спектров сигналов при свертке называется фильтрацией. Когда спектры умножаются друг на друга как комплексные числа, происходит умножение амплитуд гармоник исходного сигнала и ядра свертки (а фазы складываются).
В звукозаписи изменение спектра позволит очищать запись от шумов, компенсировать искажения сигнала, менять тембры инструментов, акцентировать внимание слушателей на отдельных партиях.
Ядро свертки при фильтрации называют фильтром. Часто так называют все устройство, осуществляющее процесс фильтрации. Длина (размер) фильтра — это длина ядра свертки.
Вейвлеты.
К настоящему времени известно свыше 4300 вейвлетов, однако, лишь простейшие вейвлеты — Вейвлеты Хаара удовлетворяют нужным условиям (1,5,6,7 требования см. ниже).
Требования к вейвлетам:
1. Вычислительная простота
2. Хорошие качества приближения
3. Вычислительная устойчивость
4. Гладкость
5. Компактность носителя у базисных вейвлетов (или быстрое убывание на бесконечность, при отсутствии такой компактности)
6. Симметричность базисных вейвлетов
7. Ортогональность вейвлетного разложения
Вейвлеты на множестве ![]() .
.
Продолжаем рассматривать дискретные сигналы. Мы рассмотрели способ построения базиса Фурье для анализа сигналов, но следует отметить его недостатки: это не локализованность в пространстве. Это означает, что векторы базиса Фурье распределены настолько «равномерно» насколько это возможно.
Мы говорим, что вектор z ![]()
![]() локализован в пространстве около
локализован в пространстве около ![]() , если большинство компонент z(n) вектора z равны нулю или по крайней мере относительно малы всюду, за исключением нескольких значений n, близких к
, если большинство компонент z(n) вектора z равны нулю или по крайней мере относительно малы всюду, за исключением нескольких значений n, близких к ![]()
Элемент ![]() базиса Фурье не локализован в пространстве около
базиса Фурье не локализован в пространстве около ![]() , потому что его компоненты
, потому что его компоненты ![]() =
=![]() имеют одинаковую амплитуду. Эта ситуация противоположна локализации.
имеют одинаковую амплитуду. Эта ситуация противоположна локализации.
В более общем случае пространственно локализованный базис полезен потому, что он гарантирует локальный анализ сигнала. Если, допустим, что некоторый коэффициент велик, то мы можем идентифицировать ту локальную область, с которой коэффициент связан.
У нас уже есть один пример локализованного базиса — это евклидов базис или так называемый, стандартный базис. Он локализован наилучшим образом, каждый базисный вектор имеет только одну ненулевую компоненту. Однако очень хотелось бы достигнуть частотной локализации, как в базисе Фурье. Т. е. линейности и инвариантности. Поэтому базисные векторы должны состоять из очень малых групп частот.
Использование частотно-локализованных базисов позволяет нам также имитировать общую технику фильтрования.
Таким образом, наша конечная цель — это получить базис, элементы которого пространственно и частотно локализованы. Тогда коэффициенты разложения векторов в этом базисе будут давать пространственную и частотную информацию.
Поэтому мы сможем совершить одновременно: частотный и временной анализ такого вектора и вейвлеты дадут нам такой базис!
Когда мы говорим об аудио сигнале, мы имеем ввиду, что вектор — функция зависит от времени. Таким образом, вектор z(t) зависит от t, где t — это время.
Также хотелось бы, чтобы переход от стандартного эвклидова базиса к новому базису B был быстрым, вычислялся с помощью быстрого алгоритма, так как от этого зависит качество решения задачи в реальном размере.
Можем использовать формулу свертки Быстрого Преобразования Фурье для быстрого изменения базиса. Возможно, это поможет.
![]()
Но существует одно наблюдение, которое нам препятствует: если новый базис ортонормированный, то мы не можем получить частотно-локализованный ортонормированный базис, т. к. его векторы будут с равными амплитудами.
Это наблюдение не настолько обескураживающее, как кажется, т. к. из него следует незначительная модификация исходной идеи и приводит к основополагающим результатам.
Для того, чтобы рассматривать один вектор, множество полных сдвигов, которого образует ортонормированный базис, мы рассмотрим два вектора со множеством сдвигов по четным периодам. Один из будет называться отцовским. Bторой, материнским вейвлетом.
Лемма 1.5.Множество ![]() ортонормировано тогда и только тогда, когда выполняется равенство
ортонормировано тогда и только тогда, когда выполняется равенство
![]() [1, с. 158]
[1, с. 158]
Определение 1.2. Предположим, что M![]() N,N=2M, u,v
N,N=2M, u,v ![]()
![]()
A(n) — это система матриц из u,v:
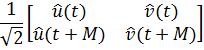
Теорема 1.4. Предположим, что M![]() N,N=2M, u,v
N,N=2M, u,v ![]()
![]() . Тогда,
. Тогда, ![]() =
=![]() ; Есть ортонормированный базис
; Есть ортонормированный базис ![]() тогда и только тогда, когда система матриц А(n) унитарна для каждого n=0,1,2,…M-1.
тогда и только тогда, когда система матриц А(n) унитарна для каждого n=0,1,2,…M-1.
Эквивалентно,
B есть вейвлет первого порядка тогда и только тогда, когда
![]()
![]()
& ![]() [1, с. 162]
[1, с. 162]
Доказательство.
Матрица унитарна тогда и только тогда, когда ее столбцы образуют ортонормированный базис в ![]() .
.
По лемме 1.5 множество ![]() ортонормировано тогда и только тогда, когда выполняется равенство
ортонормировано тогда и только тогда, когда выполняется равенство
![]()
Это означает, что первый столбец матрицы A(n) имеет длину равную 1 для n=0,1,…M-1; Далее утверждается что, ![]() =0 для всех j,k=0,1,…,M-1;
=0 для всех j,k=0,1,…,M-1;
когда выполняется равенство ![]()
Это означает, что столбцы матрицы А(n) ортогональны, следовательно, В есть ортонормированный базис ![]() .
.
В общем случае показать, что отцовский и материнский базисы являются ортонормированными не очень легко. Однако нетрудно построить их таким образом, чтобы матрицы A(n) были унитарными для всех n=0,1,…M-1;
Мы можем вычислить обратное Дискретно преобразование Фурье и получить пример вейвлет базиса первого этапа.
На ![]() и
и ![]() наложено условие, что их среднее равно 1. Это означает, что одно из слагаемых может быть равно 0. Таким образом, в один из векторов не будет иметь компоненты в направлении
наложено условие, что их среднее равно 1. Это означает, что одно из слагаемых может быть равно 0. Таким образом, в один из векторов не будет иметь компоненты в направлении ![]() (
(![]() ).
).
Это позволяет нам выделить низкие и высокие частоты. Поэтому u-это вектор, содержащий низкие частоты (низкочастотный фильтр), а v-это вектор, содержащий высокие частоты (высокочастотный фильтр).
Такое представление ведет к очень неожиданным и разнообразным результатам.
Выводы
Таким образом, мы только прикоснулись к возможностям обработки аудио сигнала.
Как мы видим Преобразование Фурье хорошо тем, что требует малых вычислительных ресурсов (речь идет об алгоритме БПФ), но его главным недостатком всегда будет нелокализованность и возникающие трудности для локального анализа сигнала. Таким образом, амплитуды всегда будут равны 1 и не будет возможности скорректировать сигнал более тщательно. Поэтому вейвлеты интересны тем, что могут создать такой базис, который будет частотно-локализован, ортонормирован, периодичен, который позволит корректировать и приближать сигнал к более качественному, более идентичному аналоговому, живому звуку. Этот раздел математики относительно новый в мире и поэтому полностью не изучен. Но природа самих вейвлетов естественным образом подталкивает и интуитивно дает понять, что у них есть большой прикладной потенциал и поэтому они требуют исследований.
Список литературы:
1.Введение в вейвлеты в свете линейной алгебры. М. Фрейзер. Издательство: Бином. Лаборатория знаний. ISBN 978-5-94774-557-3, 0-387-98639-1; 2008 г. / An Introduction to Wavelets Through Linear Algebra ISBN 978-5-94774-557-3, 0-387-98639-1; 2008 г.
2.Введение в цифровую обработку сигналов (математические основы). А. Лукин (2002 г). Издательство: Лаборатория компьютерной графики и мультимедиа, МГУ.
3.Введение в теорию вейвлетов. Ю.К. Демьянович, В.А. Ходаковский. СПб., 2007.
отправлен участнику


Оставить комментарий