РАСЧЁТ  ЭЛЕКТРИЧЕСКИХ  ЦЕПЕЙ  С  ИСПОЛЬЗОВАНИЕМ  СИСТЕМ  ЛИНЕЙНЫХ  АЛГЕБРАИЧЕСКИХ  ВЫРАЖЕНИЙ

Ли  Геннадий  Инокентиевич

студент  1  курса,  кафедра  Электроэнергетики  и  электротехники  Дальневосточного  федерального  университета,  РФ,  г.  Владивосток

E -mail:  li-gena-1996@mail.ru

Дмух  Галина  Юрьевна

научный  руководитель,  канд.  пед.  наук,  доц.  кафедры  алгебры,  геометрии  и  анализа  ШЕН  Дальневосточного  Федерального  Университета,  РФ,  г.  Владивосток

Статья  посвящена  методу  расчёта  электрических  цепей  с  использованием  систем  линейных  алгебраических  уравнений.  В  ней  рассмотрены  основные  методы  и  понятия.  Приведён  пример,  показывающий  рациональность  и  практичность  использования  систем  линейных  алгебраических  уравнений  в  электротехнике.  Так  же  рассматриваются  вопросы  взаимодействия  и  связи  математики  и  инженерии.

Инженерное  дело  тесно  связано  с  математикой.  Математические  методы  нашли  широкое  применение  в  различных  инженерных  специальностях.  Можно  сказать,  что  инженерия  стимулирует  развитие  математики,  ведь  многие  математические  методы  появлялись  из  потребностей  инженерной  практики.  Например,  метод  наименьших  квадратов,  который  используется  для  обработки  результатов  наблюдений,  возник  из  потребностей  геодезической  практики.  Цель  инженерной  математики,  помочь  инженеру  в  познании  практически  важных  моделей  и  методов,  которые  ориентированы  на  решение  различных  инженерных  задач.  Следовательно,  инженерное  дело  не  может  развиваться  и  реализоваться  без  математического  аппарата.

Например,  инженер-электротехник,  при  решении  различных  задач  использует  системы  линейных  алгебраических  уравнений  (СЛАУ).

Системой  линейных  алгебраических  уравнений  содержащей  m  уравнений  и  n  неизвестных,  называется  система  вида:

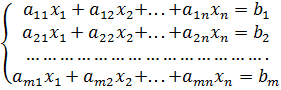
где:  числа  ,  ,    называются  коэффициентами  системы,  числа  –  свободными  членами. 

подлежат  нахождению  [1,  с.  29].

Первые  СЛАУ  встречаются  ещё  в  вавилонских  и  египетских  рукописях  II  века  до  н.  э.,  а  также  в  трудах  древнегреческих,  индийских  и  китайских  мудрецов.  В  китайском  трактате  «Математика  в  девяти  книгах»  словесно  изложены  правила  решения  систем  уравнений,  были  замечены  некоторые  закономерности  при  решении.  На  протяжении  многих  лет  выдающиеся  математики  своего  времени  разрабатывали  методы  решения  СЛАУ.  На  данный  момент  существует  множество  различных  методов  решения  систем.  В  своей  работе  я  разберу  один  из  основных  методов  решения  СЛАУ,  метод  Гаусса.

Суть  метода  заключается  в  том,  что  систему  линейных  алгебраических  уравнений  приводят  к  ступенчатому  виду,  используя  элементарные  преобразования.

Приведённая  система  имеет  ступенчатый  вид 

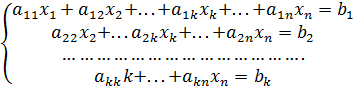
где  .  Коэффициенты    называются  главными  элементами  системы  [1,  c.  34]. 

Составив  ступенчатую  систему,  решаем  её.  Если  система  оказывается  треугольной,  то  есть  ,  то  система  имеет  единственное  решение.  Если  же  ,  то  исходная  система  имеет  множество  решений.

В  электротехнике  часто  встречаются  задачи,  в  которых  необходим  расчёт  электрической  цепи,  то  есть  необходим  расчёт  напряжения  и  силы  тока  во  всех  ветвях  цепи.  Например,  известны  сопротивления  и  ЭДС,  но  нет  значений  силы  тока.  Для  решения  таких  задач  используют  правила  Кирхгофа.

Разберём  этот  метод  на  конкретной  задаче.  При  решении  будем  использовать  метод  Гаусса.  Этот  метод  является  наиболее  простым,  и  подходит  практически  к  любой  системе.

Пример:

Дана  схема  (рисунок  1),  и  известны  сопротивления  резисторов  и  ЭДС  источников( ).  Требуется  найти  токи  в  ветвях

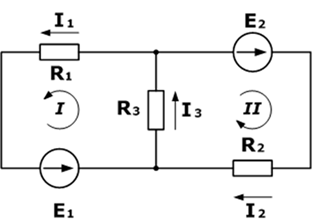
Рисунок  1.  (Схема  электрической  цепи)

Решение:

Первое  правило  Кирхгофа  гласит,  что  алгебраическая  сумма  токов,  сходящихся  в  узле,  равно  0.  Значит:    

Второй  закон  Кирхгофа:  алгебраическая  сумма  падений  напряжений  на  всех  ветвях,  принадлежащих  любому  замкнутому  контуру  цепи,  равна  алгебраической  сумме  ЭДС  ветвей  этого  контура.  С  помощью  этого  закона  составим  уравнения  для  первого  и  второго  контура  цепи: 

Теперь  из  трёх  уравнений  составляем  систему  уравнений:

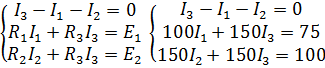
Из  коэффициентов  перед  неизвестными  составляем  матрицу:

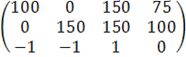
Решение  можно  разбить  на  два  этапа.  Сначала  с  помощью  элементарных  преобразований  приведём  систему  к  ступенчатому  виду:

1-ую  строку  делим  на  100: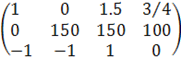 

к  3  строке  добавляем  1  строку,  умноженную  на  1: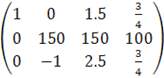 

2-ую  строку  делим  на  150: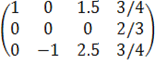 

к  3  строке  добавляем  2  строку: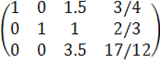 

Теперь  решаем  ступенчатую  систему:

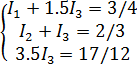
Так  как  ,  система  имеет  единственное  решение.

Находим  значения  токов:

Вычислительная  техника  выполняет  такие  операции  за  доли  секунд.  Таким  образом,  СЛАУ  играет  большую  роль  в  электротехнике.  С  помощью  СЛАУ  можно  быстро  и  точно  рассчитать  эклектическую  цепь.

Список  литературы:

1.Письменный  Д.  «Конспект  лекций  по  высшей  математике»,  Айрис-пресс,  2006,  4-е  изд.,  —  608  с.

2.Сигорский  В.П.  Математический  аппарат  инженера.  Изд.  2-е,  стереотип.  «Texнiкa»,  1977,  —  768  с.

3.Шебес  М.Р.,  Каблукова  М.В.  Задачник  по  теории  линейных  электрических  цепей:  Учеб.  пособ.  для  электротехнич.,  радиотехнич.  спец.  вузов.  4-е  изд.,  перераб.  и  доп.  М.:  Высш.  шк.,  1990.  —  544  с.