ОСЕВАЯ  ПОДАТЛИВОСТЬ  КОНИЧЕСКИХ  РОЛИКОПОДШИПНИКОВ

Масленникова  Галина  Владимировна

Угрюмов  Родион  Львович

студенты  кафедры  «Технология  машиностроения»  Механико-технологического  факультета  Московского  государственного  машиностроительного  университета  (МАМИ),  РФ,  г.  Москва

E -mail:  galincka@list.ru

Булавин  Игорь  Александрович

научный  руководитель,  канд.  техн.  наук,  доцент,  профессор  кафедры  «Технология  машиностроения»,  механико-технологического  факультета,  транспортно-технологического  института,  Московского  государственного  машиностроительного  университета  (МАМИ),  РФ,  г.  Москва

E -mail:  Bulavin-mami  @  yndex.ru

В  различных  агрегатах  машин  подшипники  качения  устанавливаются  с  зазором,  без  зазора  или  с  предварительным  натягом.  Величина  зазора  зависит  от  типа  и  размера  подшипника,  режима  работы  узла.  В  ряде  случаев  необходимы  осевые  преднатяги. 

Если  в  подшипниковых  узлах,  по  условиям  эксплуатации,  наличие  зазоров  или  значительных  упругих  смещений  колец  под  действием  внешних  нагрузок  является  недопустимым,  то  подшипники  устанавли­ваются  с  предварительным  натягом.  Преднатяг  подшипников  —  один  из  важнейших  параметров  качества  сборки  редукторов  ведущих  мостов  автомобилей  (рисунок  1).  Осевая  податливость  конических  роликоподшипников  —  это  один  из  важнейших  параметров,  определяющих  точность  регулирования  преднатяга  подшипниковых  узлов.

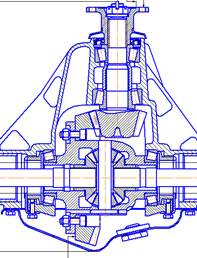
Рисунок  1.  Редуктор  ведущего  моста  легкового  автомобиля.  Подшипники  ведущей  и  ведомой  шестерни  установлены  с  осевым  преднатягом

Повышение  осевой  и  радиальной  жесткости  подшипниковых  узлов  для  обеспечения  стабильности  параметров  зацепления  шестерен  в  редукторах  достигается  это  за  счет  главной  особенности  конических  радиально-упорных  подшипников  —  нелинейной  характеристики  осевых  упругих  смещений  колец  подшипников  при  действии  осевой  нагрузки.  Нелинейный  характер  осевой  податливости  объясняется  контактом  тел,  имеющих  три  конических  поверхности  (рисунок  2).

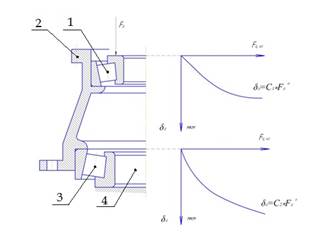
Рисунок  2.  В  дуплексе  регулируемых  подшипников  каждый  подшипник  имеет  свою  нелинейную  харатеристику  осевой  податливости  (1,3  —  подшипники  регулируемого  с  преднатягом  дуплекса,  2  —  корпус,  4  —  фальш-оправка)

В  литературе  для  конических  роликоподшипников  приводится  нелинейная  осевая  характеристика  податливости,  показывающая,  что  с  увеличением  осевой  нагрузки  на  конический  подшипник  приращение  осевого  смещения  колец  относительно  друг  друга  уменьшается.  Это  и  позволяет,  создавая  преднатяг  подшипников,  существенно  (в  десятки  и  сотни  раз)  повысить  осевую  и  радиальную  жесткость  подшипников  узлов  по  сравнению  с  отдельно  взятым  подшипником  в  состоянии  поставки.

Близко  описывает  осевое  смещение  колец  в  конических  роликоподшипниках  эмпирическая  зависимость  приведенная  в  работе  Пальмгрена  А.:

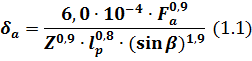
где:  —  осевая  сила  на  подшипник,  (кг), 

z  —  число  роликов;

—  длина  ролика,  (мм);

β  —  угол  наклона  наружного  кольца,  (град.). 

В  Московском  Государственном  машиностроительном  университете  (МАМИ)  получена  уточненная  эмпирическая  зависимость  для  расчета  осевого  смещения  колец  с  учетом  дополнительных  параметров  геометрии  :

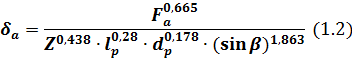
где:  —  осевая  сила  на  подшипник,  (кг),

Z  —  количество  роликов;                                                               

d  —  диаметр  роликов,  (мм);

l —  длина  роликов,  (мм);

β  —  угол  конуса  наружного  кольца,  (град.).

Результаты  расчета  и  экспериментальных  исследований  приведены  на  рисунке  3.  Так  как  подшипники  установлены  последовательно,  то  суммарная  характеристика  дуплекса  определяется  алгебраическим  сложением  двух  характеристик  (рисунок  4).  При  этом  показатель  степени  m=2/3,  определяющий  степенную  функцию  как  полукубическую  параболу  должен  быть  единым  для  каждого  из  подшипников.

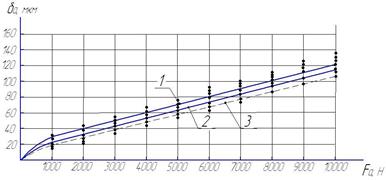а)

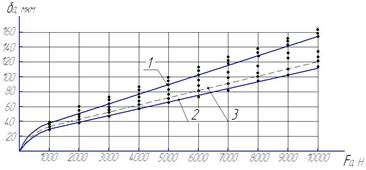б)

Рисунок  3.  Осевое  упругое  смещение  колец  в  подшипниках  7610К1  (а)  и  7613К1  (б):  кривая  1  —  аппроксимирована  по  экспериментальным  данным,  кривая  2  —  эмпирическая  формула,  3  —  теоретическая  формула

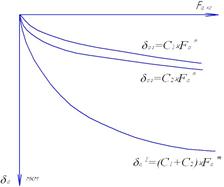
Рисунок  4.  Суммарная  жесткостная  характеристика  осевых  упругих  смещений  при  создании  преднатяга  в  дуплексе  регулируемых  подшипников

Все  экспериментальные  исследования  осевой  податливости  проводились  в  диапазоне  1000—10000Н  осевого  нагружения  с  одновременным  вращением  корпуса  с  частотой  30  мин^-1  с  использованием  специальной  установки  (рисунок  5)  на  базе  винтового  пресса.  Исследуемые  подшипники  устанавливались  на  специальной  фальш-оправке. 

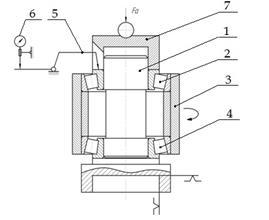
Рисунок  5.  Схема  измерения  осевого  смещения  колец  в  конических  роликоподшипниках  при  действии  осевой  нагрузки  (1  —  оправка,  2,4  —  исследуемые  подшипники  одного  типа,  3  —  фальш-корпус,  5  —  равноплечий  рычаг,  6  —  индикатор,  7  —  втулка  для  нагружения)

Для  определения  теоретической  зависимости  осевых  упругих  смещений  коническом  подшипнике  были  приняты  следующие  допущения:

1.  Осевая  нагрузка  на  подшипник  равномерно  распределяется  между  всеми  телами  качения.

2.  Между  рабочими  торцами  роликов  и  направляющим  бортом  внутреннего  кольца  зазор  отсутствует.

3.  Смещение  коле  происходит  вследствие  упругих  контактных  деформаций  в  направлении  нормальной  нагрузки  при  контакте  упругих  тел  двойной  кривизны  (величина  обратная  радиусу).

4.  Двойная  кривизна  образована  радиусами  ролика  и  радиусом  бомбины  (бочкообразности)  ролика  и  поверхностей  качения  колец  подшипника.

Из  теории  упругих  контактных  деформаций  для  контактирующих  тел  двойной  кривизны  известна  зависимость: 

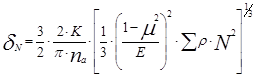,  (1.3)

где    —  табличный  коэффициент,  учитывающий  кривизну  упругих  тел  в  контакте  и  определяемый  в  зависимости  от  вспомогательной  величины  . 

(Обозначим  ).

При  контактировании  поверхностей  двойной  кривизны  (рисунок  7)  с  радиусами  R₁₁>R₁₂  и  R₂₁>R₂₂  вспомогательная  величина    определяется  по  выражению:

                                                                                                                (1.4)

где:        —  сумма  главных  кривизны  соприкасающихся  тел  в  начальной  точке  касания,

μ  —  коэффициент  Пуассона,

Е  —  модуль  упругости,

N  —  нормальная  нагрузка  в  контакте.

Осевое  смещение  колец  в  коническом  подшипнике  (рисунок  6)  представим  как  сумму  перемещений,  возникающих  за  счет  контактных  деформаций  на  поверхности  качения:

    ,  (1.5)

где:    —  это  смещение  ролика  относительно  наружного  кольца  по  оси  подшипника,

  —  смещение  внутреннего  кольца  относительно  ролика.

Нормальная  нагрузка  в  контакте  ролика  с  наружным  и  внутренним  кольцами  определяется  по  формуле:

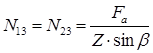,(1.6) 

где:  F_a—  осевая  нагрузка  на  подшипник,

Z  —  число  роликов  в  подшипнике.

Смещение  внутреннего  кольца  относительно  ролика  —    имеет  предел  по  силе  F_a,  при  которой  выбирается  зазор  между  торцами  роликов  и  направляющим  бортом  внутреннего  кольца.

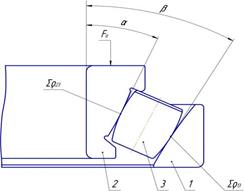
Рисунок  6.  Осевое  смещение  колец  в  коническом  подшипнике  (1  —  наружное  кольцо,  2  —  внутреннее  кольцо,  3  —  ролик)

Тогда,  подставляя  полученное  выражение  и  с  учетом  обозначений,  принятых  на  рисунке  8,  получаем  теоретическую  зависимость  для  определения  осевых  упругих  смещений  в  коническом  подшипнике:

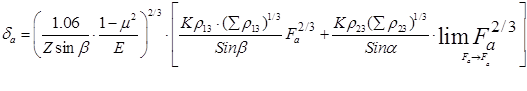,  (1.7)

где:    и    —  коэффициенты,  определяемые  по  таблице  /2/  в  зависимости  от  величин  соответственно;

  ,    —  суммы  главных  кривизны  соответственно  в  контакте  ролика  с  наружным  и  внутренним  кольцами,

  —  сила,  при  которой  выбирается  зазор  между  торцами  роликов  и  направляющим  бортом  внутреннего  кольца  подшипника.

При  сжатии  дуплекса  регулируемых  подшипников  суммарное  осевое  смещение  будет  равно  сумме  смещений  в  каждом  подшипнике.

Тогда,  представив  полученную  зависимость  в  виде  степенной  функции:.

Суммарное  осевое  смещение  внутреннего  кольца  одного  подшипника  относительно  внутреннего  кольца  другого  подшипника  в  дуплексе  будет  равно:

  ,  (1.8)

где    и    —  постоянные  коэффициенты  осевых  жесткостных  характеристик  регулируемых  подшипников,  зависящие  от  геометрии  и  определяемые  приближенно,  вследствие  малости  ,  по  выражению:

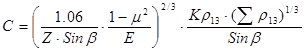  (1.9)

Табличные  величины  2K/(πn_a)  зависят  от  вспомогательного  комплексного  коэффициента  кривизны  контактирующих  поверхностей  cos  τ,  который  определяется  по  формуле:

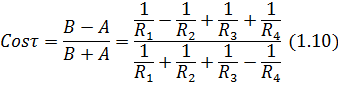
Зная  cos  τ  можно  определить  по  таблице  в  справочнике  значение  величины  2K/(πn_a).

Для  контактирующих  поверхностей  вращения  радиусами  R₁,  R₂  и  R₃,  R₄,  R₂>R₁  и  R₄>R₃  в  соответствии  с  рисунками  7  и  8.

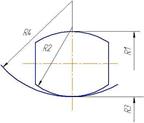
Рисунок  7.  Схема  для  определения  вспомогательного  комплексного  коэффициента  кривизны  контактирующих  поверхностей  cos   τ

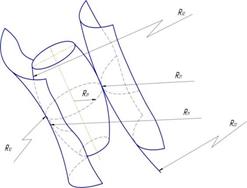
Рисунок  8.  К  определению  суммы  главных  кривизн  в  контакте

Для  компенсации  погрешностей  углов  конуса  наружного  кольца,  ролика  и  поверхности  качения  внутреннего  кольца,  рабочие  поверхности  выполняются  с  так  называемой  «бомбиной»  —  бочкообразностью.  Величина  бомбины  задается  в  технических  условиях  на  изготовление  колец  подшипников  и  находится  в  пределах  от  8  до  20  мкм.

Для  определения  кривизны  бомбинированной  поверхности  необходимо  знать  радиус  бомбины,  который  определяется  по  формуле:

где:  b  —  ширина  поверхности  качения  колец  или  роликов  (мм);

а   —  величина  бомбины  (бочкообразности)  (мм).

Определение  параметров  а  и  b  выполнялось  с  помощью  профилометра-профилографа  «Калибр-201».  Для  этого  были  записаны  с  горизонтальным  увеличением  ГУ=4  и  вертикальным  увеличением  ВУ=1000  профилограммы  поверхностей  качения  наружного  кольца,  ролика  и  внутреннего  кольца,  представленные  на  рисунке  12. 

Величина  бомбины  составляет  а=9  мкм,  у  ролика  а=22  мкм,  у  внутреннего  кольца  а=8  мкм  (рисунок  9). 

Если  поверхность  не  является  бомбинированной,  то  в  расчетах  кривизны  необходимо  принимать  радиус  ,  тогда  кривизна  этой  поверхности  в  этом  сечении  будет  равна  ρ=0.

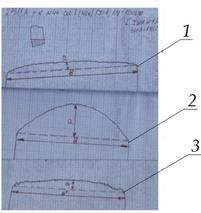
Рисунок  9.  Профилограммы  поверхностей  качения:  1  —  наружного  кольца,2  —  ролика  и  3  —  внутреннего  кольца  конического  роликоподшипника  (горизонтальное  увеличение  ГУ=4,  вертикальное  увеличение  ВУ=1000,  профилометр-профилограф  КАЛИБР-201,  а-высота  бомбины,  в-ширина  поверхности  качения

Таким  образом,  в  результате  исследований  установлено,  что  коэффициенты  осевой  податливости  имеют  диапазон  С₁+С₂=(1,0…2,5)∙10^-2  для  подшипников  с  углами  конуса  β=12⁰  и  С₁+С₂=(1,0…2,5)∙10^-3  для  подшипников  с  углами  конуса  β=30⁰.

Исследование  влияния  погрешности  формы  проведено  в  соответствии  с  разработанной  методикой  для  погрешностей:  ΔR  –  Отклонение  от  округлости  на  поверхно­сти  качения  (рисунок  10)  и  ΔТ-  торцевое  биение  наружного  кольца  относительно  оси  вращения  вала,  по  схеме  однофакторного  эксперимента.

Зависимость  математически  может  быть  описана  степенной  функцией  вида:

y=  а  ∙  х^m                                                                       (1.12)

где:  y  =  δa^ΔR  –  δa₀  —  усредненная  разность  упругих  смещений  подшипника  с  отклонением  его  округлости  в  исходном  состоянии;

х  =  ΔR/ΔR₀  —  отношение  отклонения  от  округлости  на  поверхности  качения,  образованном  в  результате  сборки  к  исходному  значению  —  ΔR₀;

a  и  m  —  постоянные  коэффициенты,  определяемые  по  формулам  мето­да  наименьших  квадратов.

Принятая  математическая  модель  позволила  получить  частную  эм­пирическую  зависимость  осевых  упругих  смещений  в  кони­ческом  подшипнике  под  нагрузкой  с  учетом  отклонения  от  округлости,  на  поверхности  качения  наружного  кольца:

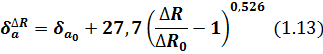
где:  ΔR  —  погрешность  формы  поверхности  качения  после  сборки  наружного  кольца  с  корпусом,  (мкм);

ΔR₀  —  допустимая  погрешность  формы  поверхности  качения  наружного  кольца  в  состоянии  поставки,  (мкм);

  —  осевая  податливость  в  коническом  подшипнике  в  состоянии  поставки,  (мкм);

27,7  —  постоянный  коэффициент.

Рисунок  10.  Круглограмма  поверхностей  качения  наружных  колец  конических  роликоподшипников  записанных  в  процессе  исследования  влияния  отклонения  от  круглости  на  осевую  податливость

  По  полученной  формуле  выполнялись  расчеты,  результаты  которых  представлены  на  графике  (рисунок  11).

Полученные  результаты,  исследования  осевого  смещения  колец  конических  роликоподшипников  редукторов  позволяют  сделать  следующие  выводы:

1.  Теоретическая  зависимость  осевой  податливости  (1.7)  в  конических  роликоподшипниках  с  углами  конуса  b=12°…30⁰  при  действии  осевой  нагрузки  получена  на  основе  теории  контактных  деформаций.

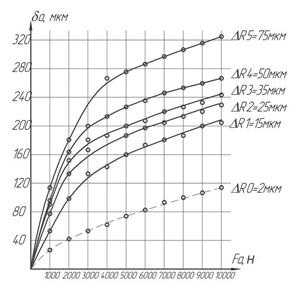
Рисунок  11.  Изменение  монтажной  высоты  конического  роликоподшипника  при  действии  осевой  нагрузки  в  зависимости  от  действительной  погрешности  формы  на  поверхности  качения  ΔR

2.  Экспериментально  получена  эмпирическая  зависимость  (1.20).

3.  Проверка  результатов  расчета  показала,  что  разброс  значений  составил  не  более  5…6  %.

4.  Экспериментально  установлено  влияние  на  осевую  податливость  в  конических  роликоподшипниках  погрешностей  сборки  на  поверхностях  качения.

5.  Осевая  податливость  в  подшипниках  при  создании  преднатяга  в  пределах  диапазона  сил  заданных  моментом  трения  составляет  0,02…0,08  мм.

6.  Полученные  пределы  осевого  сжатия  подшипников  при  создании  преднатяга  позволяют  определить  линейный  допуск  на  преднатяг  и  другие  параметры  процесса  регулирования  в  технологии  сборки.

Список  литературы:

1.Булавин  И.А.,  Груздев  А.Ю,  Будыкин  А.В.  «Технология  сборки  подшипниковых  узлов  с  предварительным  натягом  в  редукторах  ведущих  мостов  автомобилей»,  журнал  «Сборка  в  машиностроении,  приборостроении»  —  2013  г.,  —  №  6  —  стр.  32—38.

2.Булавин  И.А.,  Груздев  А.Ю,  Будыкин  А.В.  «Определение  параметров  наладки  процесса  создания  преднатяга  в  подшипниках  агрегатов  машин»,  журнал  «Автомобильная  промышленность»,  —  2013  г.,  —  №  8,  —  стр.  37—40.

3.Булавин  И.А.,  Груздев  А.Ю,  Будыкин  А.В.  «Преднатяг  подшипников  в  агрегатах  машин»,  журнал  «Технология  машиностроения»,  —  2013  г.,  —  №  3,  —  стр.  31—37.