МАТЕМАТИЧЕСКАЯ  МОДЕЛЬ  РАСЧЕТА  САМОЗАПУСКА  АСИНХРОННЫХ  ДВИГАТЕЛЕЙ  ПРИ  НЕСИНУСОИДАЛЬНОСТИ  ПИТАЮЩЕГО  НАПРЯЖЕНИЯ

Шпота  Артем  Андреевич

студент  1  курса  магистратуры,  кафедра  Электроснабжение  промышленных  предприятий,  Омский  государственный  технический  университет,  РФ,  г.  Омск

Art -93-sh@yandex.ru

Планков  Александр  Анатольевич

научный  руководитель,  канд.  техн.  наук,  старший  преподаватель,  кафедра  Электроснабжение  промышленных  предприятий,  Омский  государственный  технических  университет,  РФ,  г.  Омск

Индивидуальный  выбег  при  наличии  близкого  КЗ,  что  имеет  место  для  расчетного  случая,  происходит  по  более  крутой  характеристике,  чем  при  свободном  выбеге  так  как  двига­тель  переходит  в  генераторный  режим.  В  асинхронном  двигателе,  вследствие  быстрого  затухания  эдс,  тормозной  момент  практически  не  вызывает  дополнительного  торможения  и  в  расчетах,  как  правило,  не  учитываются.

Таким  образом,  расчет  индивидуального  выбега  без  учета  электромагнитных  переходных  процессов  связан  с  решением  дифференциаль­ного  уравнения  движения,  которое  может  быть  записано  в  виде:

;

или  .

Ввиду  гладкости  функции    для  решения  уравнения  могут  быть  использованы  простые  методы  численного  интегрирования  дифференциальных  уравнений,  например,  метод  Эйлера.  Конечной  целью  расчета  выбега  является  построение  кривых  выбега  и  нахождение  скорости  элек­тродвигателей  к  моменту  восстановления  питания.

При    можно  получить  кривую  выбега  в  виде:

,

где    —  начальная  частота  вращения.

Практически,  если  время  перерыва  питания  или  КЗ  меньше    в  пять  и  более  раз,  можно  пользоваться  формулой  независимо  от  харак­тера  момента  сопротивления  механизма.

При  численном  решении  методом  Эйлера  алгоритм  решения  строится  на  последовательности  временных  интервалов  .  Так  при  решении  урав­нения  находится  приращение  скольжения  на  каждом  ин­тервале:

,

где    находится  по  формуле  и  скольжение  в  начале  следующего  интервала    находится  как:

.

Расчет  разгона  электродвигателей.  Процесс  разгона  после  восстановления  питания  анализирует­ся  с  помощью  уравнения  движения

,

где  ∆m  —  избыточный  момент  на  валу  двигателя.

Время  самозапуска  может,  быть  определено  интегрированием  уравнения  (3.9)  методом  Эйлера,  который  основан  на  замене  уравнения  движения  соотношением

,

где:    —  конечные  приращения  скольжения  и  времени;

  —  значение  избыточного  момента  в  рассматриваемом  интер­вале  частоты  вращения.

Расчет  процесса  разгона  электродвигателей  с  момента  восстановления  питания  связан  с  решением  системы  дифференциальных  уравнений,  является  принципиально  групповым  и  производится  в  следующей  последовательности  [1]:

1.  Определяются  индуктивные  сопротивления  трансформатора  и  дру­гих  элементов,  расположенных  между  источником  питания  и  сборными  шинами,  к  которым  подключены  рассматриваемые  двигатели,  а  так  же  находятся  сопротивления  двигателей  в  зависимости  от  скольжения,  приведенные  к  базисным  условиям.

2.  Определяется  эквивалентное  сопротивление  двигателей,  участвующих  в  самозапуске  при  :

  .

3.  Находится  напряжение  двигателей  в  момент  подачи  питания,  т.  е.  в  момент  начала  самозапуска:

  .

4. Рассчитываются  вращающий  момент  и  момент  сопротивления  каждого  двигателя,  участву­ющего  в  самозапуске  при  этом  можно  использовать  формулы.

5. Определяется  избыточный  момент  на  валу  каждого  двигателя:

.

Быстрее  всех  запустится  двигатель,  у  которого  больше  отношение  .

6. Находится  приращение  скольжения    на  интервале  ∆t:

.

Скольжение  в  начале  следующего  интервала  времени  будет  определяться  так:

  .

На  каждом  последующем  интервале  времени  процесс  повторяется,  начиная  с  пункта  2  при  новом  значении  скольжения.  При  этом  напряжение  на  шинах  электродвигателей  повышается,  что  облегчает  самозапуск.

По  достижению  одним  из  двигателей  номинального  скольжения  двигатель  вводится  в  расчет  своим  .  Если  избыточный  момент  на  валу  одного  или  нескольких  двигателей  получается  отрицательным,  то  самозапуск  оказывается  или  затянутым,  или  невозможным  вообще.  В  этом  случае  необходимо  выяснить  условия,  при  которых  самозапуск  будет  обеспечен.  То  есть  необходимо  решить  вопрос  о  возможнос­ти  уменьшения  времени  перерыва  питания,  целесообразности  отклю­чения  части  электродвигателей  или  их  разгрузки  и  снова  рассчитать  процесс  самозапуска.  Расчет  заканчивается  при  достижении  всеми  двигателями  установившегося  значения  скольжения. 

Полное  время  самозапуска  двигателей  определяют  как  сумму  отдельных  интервалов  времени. 

Известно,  что  при  наличии  ВГ  значения  активного  сопротивления  увеличиваются  пропорционально  ,  а  реактивного-пропорционально    (где  ν  —  номер  ВГ)

 ,

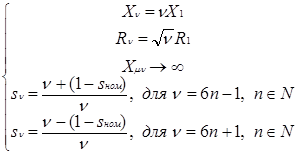где:  R₁  и  Х₁  —  активное  и  реактивное  сопротивление  на  основной  частоте;

R _ν  и  Х_ν  —  активное  и  реактивное  сопротивление  на  частоте  ВГ;

Х_μν   —  индуктивное  сопротивление  ветви  намагничивания  на  частоте  ВГ.

На  характер  изменения  скорости  при  самозапуске  оказывают  влияние  массогабаритные  параметры  АД

,

где:  T_j  —  электромеханическая  постоянная  времени;

m ʹ_дв  —  момент,  развиваемый  АД  с  учетом  ВГ.

При  самозапуске  более  легкого  АД  для  выхода  на  номинальную  скорость  вращения  потребуется  меньше  времени  по  сравнению  с  более  тяжелым  АД,  при  этом  характер  изменения  скорости  будет  носить  колебательный  характер  (рисунок  1).

Рисунок  1.  Влияние  массогабаритных  параметров  АД  на  характер  изменения  его  скорости  при  самозапуске

У  АД  с  большим  значением  момента  инерции  колебания  скорости  вращения  при  самозапуске  будут  менее  заметны,  однако  увеличение  массогабаритных  параметров  АД  приведет  к  значительному  увеличению  времени  самозапуска  АД  (рисунок  2).

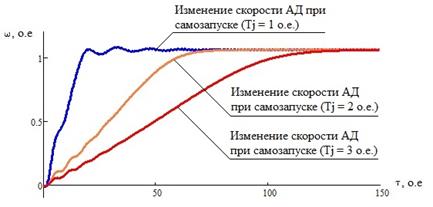
Рисунок  2.  Влияние  массогабаритных  параметров  АД  на  характер  изменения  его  скорости  при  самозапуске

Далее  выполняется  проверка  необходимости  учета  несинусоидальности  при  исследовании  устойчивости  узлов  нагрузок  СЭС

.

В  случае  одновременного  выполнения  предложенных  критериев  учета  несинусоидальности  момент  АД  определяется  по  формуле  [4]

.

При  расчете  несинусоидальных  режимов  СЭС,  как  правило,  не  учитывается  нагрев  токоведущих  частей,  что,  может  привести  к  погрешностям  при  определении  потерь  мощности  и  электроэнергии  в  элементах  сети.

Допустимость  несинусоидальности  напряжения,  питающего  двигатель,  зависит  главным  образом  от  дополнительного  его  нагрева  [2],  возникающего  вследствие  дополнительных  потерь  мощности  [3].

Установлено,  что  несинусоидальность  питающего  напряжения  приводит  к  увеличению  времени  самозапуска  АД  (рисунок  3),  что  в  итоге  увеличивает  нагрев  АД.

Рисунок  3.  Изменение  времени  самозапуска  АД  при  учете  несинусоидальности

Время  самозапуска  АД  при  k_U  =  0  %:  t₀  =  5,18  с.

Температура  нагрева  АД  при  k_U  =  0  %:  T₀  =  23,7  ⁰С.

Время  самозапуска  АД  при  k_U  =  12  %:  t₁₂  =  6,39  с.

Температура  нагрева  АД  при  k_U  =  12  %  :  T₁₂  =  26,4  ⁰С.

Список  литературы:

1.Веников  В.А.  Переходные  электромеханические  процессы  в  электрических  системах:  Учеб.  для  электроэнергет.  спец.  вузов.  4-е  изд.,  перераб.  и  доп.  М.:  Высш.  шк.,  1985.  —  536  с.,  ил.

2.Винокуров  М.Р.  Повышение  точности  расчета  вращающего  момента  асинхронного  двигателя  с  учетом  поверхностоного  эффекта  в  стержнях  ротора  [Текст]  /  М.Р.  Винокуров,  А.А.  Моисеенко,  Н.Ю.  Масловцева  //  Вестник  Донского  государственного  технического  университета.  —  2011.  —  Т.  11,  —  №  5  (56).  —  С.  621—629.

3.Куликов  Ю.А.  Переходные  процессы  в  электрических  системах:  учеб.  пособие  /  Ю.А.  Куликов.  Изд.  2-е,  испр.  и  доп.  Новосибирск  :  Изд-во  НГТУ,  2006.  —  284  с.  —  («Учебники  НГТУ»).

4.Мустафаев  Р.И.  Разработка  трехфазной  математической  модели  асинхронного  двигателя  [Текст]  /  Р.И.  Мустафаев,  Р.А.  Саидов,  Л.Г.  Гасанова  //  Проблемы  энергетики.  —  2007.  —  №  4.  —  С.  19—22.