Статья опубликована в рамках: XXVII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 16 декабря 2014 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ИЗОБРАЖЕНИЙ
Мифтахутдинов Динар Ильдусович
студент 1 курса магистратуры, факультет технической кибернетики и информатики, КНИТУ-КАИ им. А.Н. Туполева, РФ, г. Казань
E -mail: mdi_55@mail.ru
Ризаев Ильдус Султанович
научный руководитель, канд. техн. наук, профессор каф. АСОиУ, КНИТУ-КАИ им. А.Н. Туполева, РФ, г. Казань
В данной статье рассмотрены вопросы геометрической обработки изображений. Материал базируется на работах, приведенных в списке источников, в основном на монографии.
Важность указанных вопросов связана с тем, что обнаружение и распознавание объектов в бортовой системе летательного аппарата основана на оценке их характеристик на изображениях.
Процесс геометрической обработки можно выполнять в два этапа. На первом этапе выполняются сложные в вычислительном отношении координатные преобразования, описываемые функциями x = F(m, n), y = G (m, n). Эти преобразования производятся для ограниченного числа точек, расположенных в узлах регулярной прямоугольной решетки плоскости исходного изображения. Число узловых точек можно выбрать значительно меньше их общего количества, получив приемлемое время преобразования. На втором этапе в пределах отдельных фрагментов выполняются массовые координатные преобразования всех элементов изображения по простейшим, обычно линейным, функциям. Такие преобразования называют поэлементными.
Для поэлементных преобразований используются следующие подходы [1]:
1. Приближение функции в окрестностях узловой точки рядом Тейлора;
2. Кусочно-аффиное приближение;
3. Кусочно-билинейное приближение.
Наиболее оптимальным является подход, основанный на кусочно-билинейном преобразовании.
Если рассматривать пространственную привязку изображений, то наиболее быстро пространственная привязка изображений осуществляется с использование систем ГЛОНАСС/GPS. Однако из-за ошибок измерения навигационных параметров в этом случае необходимо решать задачу уточнения пространственной привязки изображений. Принципиально важным здесь является выбор механизма фильтрации вектора положения, вектора скорости и вектора ориентации летательного аппарата.
Один из подходов основан на фильтрации непосредственно самих измерений, полученных посредством систем ГЛОНАСС/GPS, по методу наименьших квадратов [3]. Этот метод дает оптимальные по точности оценки при допущении, что ошибки измерений подчинены нормальному закону и имеют нулевые математические ожидания. В этом случае проводят 2K + 1 измерений искомого параметра, считая, что отсчеты имеют номера от –K до K. Затем методом наименьших квадратов находят постоянный коэффициент полинома 2-го порядка, который принимают в качестве значения параметра в нулевой момент времени. Этот подход позволят получить быстрый алгоритм вычислений.
В качестве опорной координатной информации для привязки изображений могут выступать высокоточные электронные карты [3]. В этом случае процесс привязки базируется на автоматической или автоматизированной идентификации объектов карты (обычно это речная сети и береговые линии морей и озер) с одноименными объектами на изображении. Данный подход уступает по оперативности решению аналогичной задачи по данным систем ГЛОНАСС/GPS, но позволяет выполнять ее практически с точностью, определяемой разрешающей способностью изображения и точностью карты. Кроме того, он отличается высокой степенью автономности.
При использовании электронных карт на них выделяются опорные точки, которые затем ищутся на изображении. В результате устанавливается соответствие между опорными точками изображения и электронной карты, на основе которого определяются картографические координаты остальных точек на изображении.
В случае реализации автоматической процедуры привязки изображения к электронной карте, как правило, применяются корреляционно-экстремальное совмещение контуров [2].
Современные системы дистанционного зондирования Земли, используемые для решения разведывательных и навигационных задач, широко применяют метод одновременной съемки земной поверхности в нескольких спектральных диапазонах.
При комплексировании синхронно формируемых изображений необходимо решить задачи геометрического объединения и фотометрического выравнивания. В результате формируется суммарное изображение, которое является либо улучшенным за счет использования множества спектральных диапазонов, либо за счет многократного увеличения полосы обзора.
Пусть необходимо выполнить комплексирование изображений для увеличения полосы обзора. Опишем изображения, формируемые в результате синхронной съемки, как Bi(mi, ni), i = 1, …, I, mi = 1, …, M, ni = 1, …, N, где i — номер изображения, I ≥ 2 — число сканирующих устройств. Эти изображения регистрируются в различных системах координат (mi, ni) и имеют небольшие перекрытия по координате mi. Необходимо на основе объединения Bi(mi, ni), i = 1, …, I, сформировать в заданной картографической проекции изображение D(x, y), x = 1, …, X, y = 1, …, Y, соответствующее случаю съемки некоторым виртуальным датчиком с многократно расширенной полосой обзора [4]. Из-за неточности измерения параметров юстировки датчиков и смещения их полей зрения в общих областях имеются взаимные нелинейные геометрические искажения. Поэтому для получения общего изображения, охватывающего суммарную область наблюдения всех датчиков, необходимо устранить общие и относительные геометрические искажения, присущие сканерной съемке.
Возможны три различные технологии получения единого кадра по серии синхронно формируемых снимков [4].
1. Одно из исходных изображений выбирается в качестве базового, и далее к нему последовательно присоединяются все остальные. Функции геометрической коррекции определяются на основе координат одноименных точек, принадлежащих областям перекрытия. На втором этапе суммарное изображение преобразуется в заданную картографическую проекцию.
2. Вначале выполняется геометрическая нормализация исходных изображений, при которой учитываются детерминированные искажающие факторы. Затем для полученных изображений на основе одноименных точек определяются параметры функций геометрического преобразования и осуществляется последовательное совмещение нормализованных снимков в плоскости единого кадра.
3. На основе сопоставления множества одноименных точек вместо определения функций геометрического соответствия производится уточнение углов взаимной ориентации датчиков в некоторой общей системе координат. Поскольку эти углы остаются неизменными как в общей плоскости, так и на краях присоединяемых изображений, то следует ожидать более высокой точности совмещения на всей плоскости суммарного изображения. Кроме того, такой подход позволяет объединить процедуры геометрического совмещения и нормализации исходных изображений.
Процессы формирования и координатной обработки данных от различных датчиков описываются преобразованиями, определяемые функциями опроса датчика t = St(m, n) и сканирования сцены r = Sr(t); законом движения летательного аппарата η = Sη(t); функцией изменения вектора сканируемой точки R = SR(r, η); функциями преобразования координат сканируемой точки в геодезическую систему λ = Sλ(R), φ = Sφ(R) и функциями преобразования геодезических координат в картографические x = Sx(λ, φ), y = Sy(λ, φ) [4].
В этом случае процесс преобразования (mi, ni) в (λ, φ) можно описать как
λ = Fλ(mi, ni; ψi, θi), φ = Fφ(mi, ni; ψi, θi), i = 1, …, I, (1.1)
где: ψi = (αуi, ωуi, χуi) — вектор установочных углов i-го датчика;
θi = (αi, ωi, χi) — вектор углов ориентации летательного.
Установочные углы не изменяются во времени и определяют направление системы координат датчика по отношению к конструктивным осям летательного аппарата. Углы ориентации самолета изменяются во времени, и их значения передаются вместе с видеоданными. Поскольку одноименные точки, находящиеся в перекрывающихся частях изображений, формируются различными датчиками в различное время, то в общем случае ψi ≠ ψi+1, θi ≠ θi+1.
Аналогично выражениям (5.1) можно определить функции геометрической обработки изображений Bi(mi, ni), i = 1, …, I, т. е. функции их преобразования в картографическую систему координат:
x = F(mi, ni; ψi, θi), y = G(mi, ni; ψi, θi), i = 1, …, I. (1.2)
Любые две одноименные точки изображений Bi(mi, ni) и Bi+1(mi+1, ni+1), сформированные датчиками Дi и Дi+1, при точном описании функций Fλ, Fφ, F, G и абсолютно точном измерении векторов ψi, ψi+1, θi, θi+1 должны иметь одни и те же геодезические (λ, φ) и картографические (x, y) координаты.
В процессе геометрического трансформирования элементы совмещаемых изображений Bi(mi, ni) и Bi+1(mi+1, ni+1) проектируются в плоскость xy в виде двух объединяющихся множеств Di и Di+1, элементы которых составляют часть суммарного изображения D(x, y):
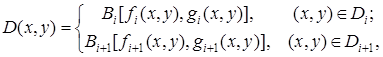 (1.3)
(1.3)
где функции fj(x, y) = mj, gj(x, y) = nj — функции обратного координатного соответствия (x, y) ↔ (m, n), рассмотренные ранее.
Функции обратного координатного соответствия можно также представить в виде:
![]()
Таким образом, зная значения векторов углов ориентации датчиков и самолета можно выполнить геометрическое совмещение изображений.
Список литературы:
1.Злобин В.К., Еремеев В.В. Обработка аэрокосмических изображений. М.: ФИЗМАТЛИТ, 2006. — 288 с.
2.Лурье И.К., Косиков А.Г. Теория и практика цифровой обработки изображений/Дистанционное зондирование и географические информационные системы. Под ред. А.М. Берлянта. М.: Научный мир, 2003. — 168 с.
3.Ризаев И.С. Геоинформационные системы: учебное пособие / И.С. Ризаев. Казань: Изд-во Казан.гос.техн.ун-та,2013. — 139 с.
4.Шовенгердт Р.А. Дистанционное зондирование. Модели и методы обработки изображений. М.: Техносфера, 2010. — 560 с.
дипломов


Оставить комментарий