Статья опубликована в рамках: XXVII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 16 декабря 2014 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АНАЛИЗ ОСОБЕННОСТЕЙ ОРГАНИЗАЦИИ НЕЙРОННЫХ СЕТЕЙ
Гаглоева Марина Валерьевна
студент 2 курса, кафедра информационных систем в экономике Северо-Кавказского горно-металлургического института (государственного технологического университета, РФ, г. Владикавказ
Авосопянц Наринэ Владимировна
студент 2 курса, кафедра информационных систем в экономике Северо-Кавказского горно-металлургического института (государственного технологического университета), РФ, г. Владикавказ
E-mail : nari5555@mail.ru
Гаглоева Индира Эдуардовна
научный руководитель, канд. техн. наук, ассистент кафедры информационных систем в экономике Северо-Кавказского горно-металлургического института (государственного технологического университета), РФ, г. Владикавказ
Интеллектуальный анализ данных представляет собой процесс обработки разнородных данных и выявления в них скрытых закономерностей, помогающих принимать решения. В связи с лавинообразным возрастанием объема информации в различных отраслях человеческой деятельности методы интеллектуального анализа данных получили наибольшую актуальность. К основным методам интеллектуального анализа данных относятся: искусственные нейронные сети, генетические алгоритмы, нечеткие множества [1].
В настоящее время технология интеллектуального анализа данных содержит множество различных подходов обнаружения знаний. Одним из эффективных методов при решении подобных задач является применение искусственных нейронных сетей.
Нервная система человека состоит из множества нейронов характеризуется большой степенью сложности, так как примерно 1011 нейронов участвуют в примерно 1015 передающих связях. Нейрон обладает уникальной способностью приема, обработки, а также передачи сигналов по нервным путям, которые образуют коммуникационную систему мозга.
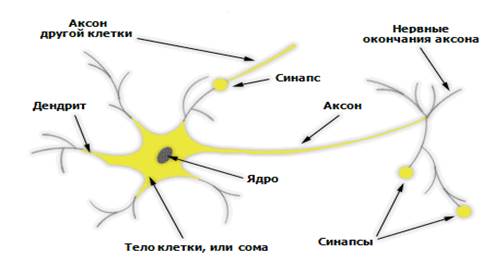
Рисунок 1. Биологический нейрон
На рисунке 1 приведена структура биологического нейрона. Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие — воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам [2; 3].
В настоящее время большое внимание уделяется вопросам исследований искусственных нейронных сетей, так как с помощью нейронной сети можно смоделировать работу нервной системы, а также ее способность обучаться и исправлять ошибки.
Составной частью нейронной сети является нейрон, в состав которого входят сумматоры, умножители и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи, веса синапсов.
На рисунке 2 представлена структура искусственного нейрона.
Сумматор выполняет сложение сигналов, поступающих по синоптическим связям от других нейронов или внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента — выхода сумматора. Это функция называется «функцией активации» или «передаточной функцией» нейрона [4].
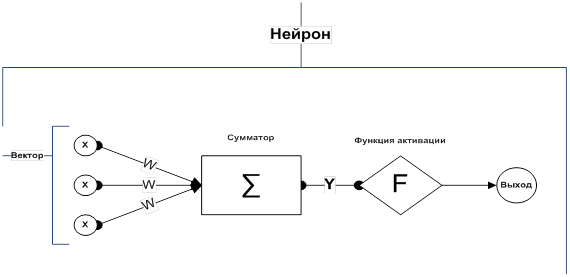
Рисунок 2. Структура искусственного нейрона
Математическая модель нейрона описывается выражением (1).
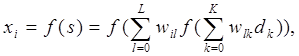 (1)
(1)
где: dk — компонент входного вектора![]() ;
;
wlk — весовые коэффициенты между входным и скрытым слоями ![]() ;
;
wil — весовые коэффициенты между скрытым и выходным слоями ![]() ;
;
L — число нейронов в скрытом слое;
f (s) — функция активации;
xi — выходной сигнал.
При моделировании нейронных сетей могут быть использованы различные типы архитектур, такие как самоорганизующиеся сети Хемминга и Хопфилда, сети Кохонена, рециркуляционные, рекуррентные, встречного распознания и др. На рисунке 3 рассмотрена структура многослойного персептрона и схема преобразования множества входных данных dk в правильный выходной сигнал xi.
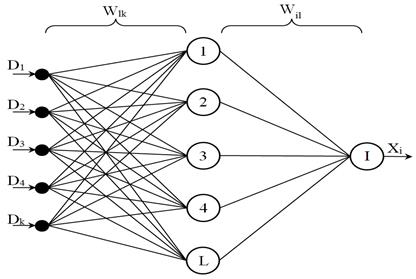
Рисунок 3. Схема преобразования входных данных
Для каждого входного сигнала заранее экспериментальным путем определяется количество нейронов на входе, на выходе имеется один нейрон, отражающий конечный результат.
Таким образом, на вход нейронной сети подается k-мерный вектор Dk. Оптимальное количество нейронов в скрытом слое L подбирается экспериментально. Выражение (1) описывает результат классификации множества входных сигналов Xi=Xi(Dk).
Наиболее распространенные функции активации нейронных элементов приведены в таблице 1.
Таблица 1.
Перечень функции активации нейронов
|
Наименование функции |
Функция |
Область значений |
|
Пороговая бинарная |
|
0, 1 |
|
Пороговая биполярная |
|
-1, 1 |
|
Сигмоидная |
|
[0, 1] |
|
Полулинейная |
|
|
|
Линейная |
f(S) = kS |
|
|
Радиальная базисная |
|
(0, 1) |
|
Полулинейная с насыщением |
|
(0, 1) |
|
Линейная ограниченная |
|
(-1,1) |
|
Гиперболический Тангенс |
|
(-1,1) |
|
Модифицированная Пороговая |
|
-1, 1 |
|
Биполярная сигмоидная |
|
[-1,1] |
|
Треугольная |
|
(0, 1) |
Применение различных функций активации определяется классом решаемых нейронной сетью задач.
Наибольшее распространение получила сигмоидная функция активации нейронов, так как является монотонной и всюду дифференцируемой, т. е. непрерывной, возрастающей функцией в диапазоне значений [0, 1]. Данная функция описывается формулой:
![]() (2)
(2)
Таким образом, многослойный персептрон с сигмоидной функцией активации нейронов способен аппроксимировать любую функциональную зависимость.
Важным этапом при построении нейросетовой модели является выбор алгоритма обучения. Можно выделить три основных вида алгоритма [2; 3]:
1. алгоритмы инициализации, которые относятся к методам, инициализирующим веса нейронной сети до ее обучения;
2. контролируемое обучение (с учителем), при котором изменяются веса, используя наборы обучающих выборок, включающих входные значения и известные значения выходов;
3. неконтролируемое обучение (без учителя), при котором веса изменяются, используя наборы входов.
Рассматриваемая многослойная нейронная сеть прямого распространения обучается с учителем. Это означает, что должно быть задано множество пар векторов:{dn, gn}, где {dn} — формализованное условие задачи, а{gn} — известное решение (истинный выход) для этого условия.
Совокупность пар {dn, gn} составляет обучающее множество.
Количество элементов в обучающем множестве N — должно быть достаточным для обучения сети, чтобы под управлением алгоритма сформировать набор параметров сети, дающий нужное отображение D→X.
Задача обучения нейронной сети сводится к подбору таких значений весов сети, чтобы ошибка была минимальна для данного обучающего множества {dn, gn}. Каждый раз, когда входной вектор от учебного набора применен к сети, сеть производит фактический выход. Мы можем таким образом определить квадратичную ошибку для этого входного вектора, суммируя квадратичные ошибки в каждом узле выхода:
![]() (3)
(3)
Процесс обучения рассматривается как задача многомерной оптимизации, которая состоит в поиске оптимальных значений весовых коэффициентов w. Главная задача в обучение нейронной сети, это минимизировать квадратичную ошибку. Мы может также определить полную квадратичную ошибку ![]() , суммируя все пары входа — выхода в учебном наборе [5]:
, суммируя все пары входа — выхода в учебном наборе [5]:
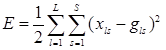 (4)
(4)
Рассмотрим узел s в скрытом слое, его выход характеризуется функцией f(nets), где nets является суммой выходов входного слоя:
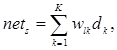 (5)
(5)
Для минимизации квадратичной ошибки, будем использовать алгоритм градиентного спуска. Определим, какое направление является «скоростным спуском» на поверхности ошибок и изменим каждый вес w так, чтобы мы двигались в этом направление. Математический это означает, что каждый вес w будет изменен на небольшое значение dw в направлении уменьшения E:
![]() (6)
(6)
где: ![]()
w (t) — вес во время t;
w (t+1) — обновленный вес.
Выражение (2.4) называется обобщенным дельта-правилом. Чтобы выполнить градиентный спуск, необходимо найти частную производную ![]() каждого веса.
каждого веса.
Для корректировки весов, между скрытым и выходным слоем, нужно найти частную производную, для каждого узла выходного слоя.
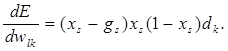 (7)
(7)
Таким образом мы нашли частную производную ошибки E по весам ![]() и можем использовать этот результат в уравнение (2.4), чтобы выполнить градиентный спуск для всех весов между скрытым и выходным слоям.
и можем использовать этот результат в уравнение (2.4), чтобы выполнить градиентный спуск для всех весов между скрытым и выходным слоям.
Теперь рассмотрим веса, между входным слоем и скрытым слоем.
 (8)
(8)
 (9)
(9)
Таким образом мы нашли частную производную ошибки ![]() по весу на основе известных величин.
по весу на основе известных величин.
В процессе экспериментов должны быть подобраны параметры, при которых достигаются приемлемые параметры скорости сходимости и качества решения.
Выбор структуры нейронной сети осуществляется в соответствии с особенностями и сложностью задачи. Для решения отдельных типов задач уже существуют оптимальные конфигурации. Если же задача не может быть сведена ни к одному из известных типов, приходится решать сложную проблему синтеза новой конфигурации.
Список литературы:
1.Рассел С., Норвиг П. Искусственные интеллект. Современный подход. М.: Изд-во «Вильямс», 2006. — 1408 с.
2.Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. М.: Горячая линия — Телеком, 2008. — 452 с.
3.Хайкин С. Нейронные сети: полный курс. М.: Изд-во «Вильямс», 2006. — 1104 с.
4.Кудухов А.Н. Гаглоева И.Э. Анализ особенностей обучения нейронных сетей // I Международная научно-практическая конференция «Проблемы и перспективы современной науки». Ставрополь: 2014. — С. 162—166.
5.Кудухов А.Н. Анализ структуры организации нейронных сетей // Труды молодых ученых. Владикавказ: Изд-во «Терек», — 2013, — Т. 4. — С. 96—101.
дипломов


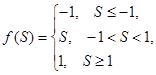
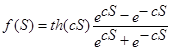
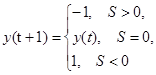
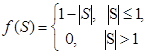
Оставить комментарий