Статья опубликована в рамках: XXVI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 18 ноября 2014 г.)
Наука: Технические науки
Секция: Энергетика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ В ЭЛЕКТРОЭНЕРГЕТИКЕ
Сикорский Сергей Петрович
E -mail: sikorskiysp@mail.ru
Ковалев Глеб Александрович
E-mail:
Батурина Екатерина Александровна
E -mail: katyonok2203.com@rambler.ru
студенты 2 курса, кафедра электроснабжения промышленных предприятий ОмГТУ, РФ, г. Омск
Осипов Дмитрий Сергеевич
научный руководитель, канд. техн. наук, доцент ОмГТУ, РФ, г. Омск
С развитием вычислительной техники создаются новые устройства, обеспечивающие функционирование электроэнергетических систем. Работоспособность данный устройств обеспечивается алгоритмически. В основе алгоритмического обеспечения лежат методы математического анализа нестационарных систем. В последние годы набирает популярность вейвлетный анализ сигнала (ВА) или вейвлет-преобразование (ВП).
Вейвлет-преобразование — интегральное преобразование, представляющее свертку вейвлет-функции с сигналом. Это способ преобразования функции (или сигнала) в форму, которая или делает некоторые величины данного сигнала более доступными для изучения. Понятие вейвлета — обобщённое название математических функций определенной формы, которые локальны во времени и по частоте и в которых все функции получаются из одной базовой, изменяя её (сдвигая, либо растягивая её).
С помощью ВП удобно решать многие практические задачи. В основном ВП применяется для анализа и обработки сигналов и функций, не постоянных во времени, когда результаты должны содержать координаты, до которых проявляются различные группы частотных составляющих или при быстрых изменениях частотных составляющих сигнала.
Непрерывное вейвлет-преобразование определяется следующим образом:

где: ![]() — функция преобразования, называющаяся материнским вейвлетом
— функция преобразования, называющаяся материнским вейвлетом
![]() — параметр сдвига
— параметр сдвига
![]() — параметр масштаба
— параметр масштаба
Преобразованный сигнал есть функция двух переменных, tau и s, параметры сдвига и масштаба, соответственно. psi(t) — функция преобразования, называющаяся материнским вейвлетом [2].
По сравнению с разложением в ряды Фурье вейвлеты способны с гораздо более высокой точностью представлять локальные особенности сигналов [1, с. 19].
Выделим основные достоинства и недостатки ВП:
Достоинства:
· Вейвлетные преобразования обладают всеми теми достоинствами, что и преобразования Фурье.
· Вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени.
· Базисные вейвлеты могут реализоваться функциями различной гладкости.
Недостатки:
· Сложность преобразования.
Анализ качества электроэнергии
Методы ВП непостоянных во времени сигналов можно использовать для определения качества электроэнергии.
На рис. 1 и рис. 2 в качестве примера были приведены выполненные авторами настоящей статьи результаты исследования в среде Matlab отчетов осциллограммы напряжения при действии возмущения.
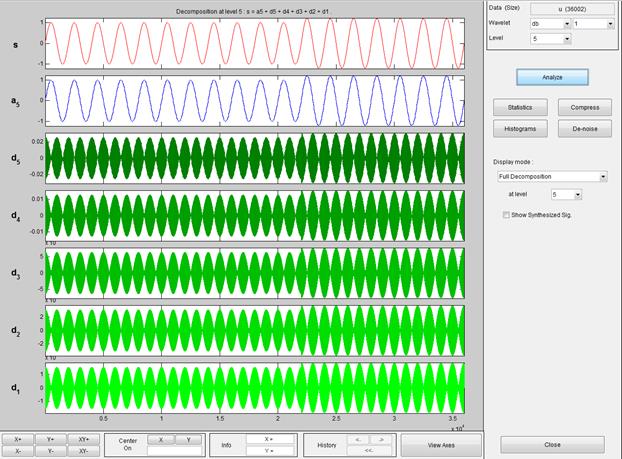
Рисунок 1. Вейвлет коэффициенты сигнала напряжения при включении линейной нгрузки
Для анализа энергетических переходных процессов использовались вейвлеты Добеши. Метод исследования основан на использовании вейвлетов при построении схем замещения линейных элементов ЭЭС, а также ВП интегро-дифференциальных уравнений, модулирующих более сложные элементы ЭЭС. Применение ВП приводит к ряду алгебраических уравнений для полной сети. Их решение представляется в терминах вейвлет- коэффициентов для напряжения в узлах сети. Фактические напряжения могут быть восстановлены через обратное ВП.
Одна из главных идей вейвлетного представления сигналов на различных уровнях декомпозиции (разложения)
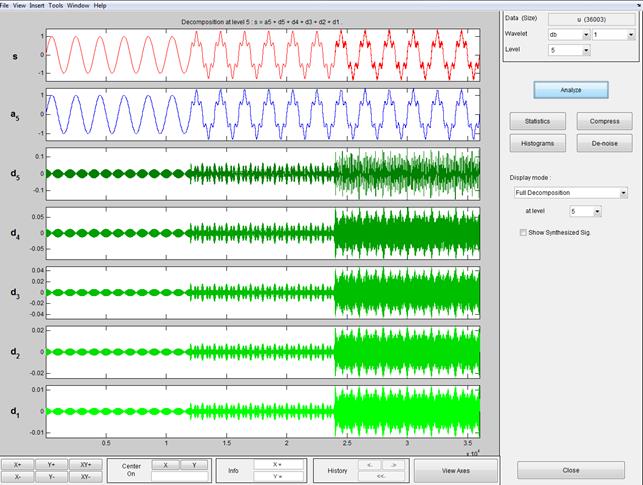
Рисунок 2. Вейвлет коэффициенты сигнала напряжения при включении в сеть нелинейной нагрузки (при наличии высших гармоник в кривой напряжения)
заключается в разделении функций приближения к сигналу на аппроксимирующую — грубую, с достаточно медленной временной динамикой изменений, и детализирующую — с локальной и быстрой динамикой изменений на фоне плавной динамики [1, с. 19].
В общем случае процесс идентификации и классификации переходных процессов в ЭЭС с помощью ВП может быть реализован путем разложения осциллограмм токов и напряжений на фундаментальные компоненты и представления их суммой базовых вейвлетных функций [1, с. 19].
Заключение
Следует отметить, что ВП открывает новые возможности и технические решения, способствует развитию и совершенствованию электроэнергетических систем. Оно может быть применено во многих областях электроэнергетики.
Список литературы:
1.Мисриханов А.М. Применение методов вейвлет-преобразования в электроэнергетике // Автоматика и телемеханика — 2006. — № 5 — С. 19.
2.Robi Polikar // The wavelet tutorial (Введение в вейвлет-преобразование, автор перевода — В.Г. Грибунин) [Электронный ресурс] — Режим доступа. — URL: http://www.autex.spb.su/download/wavelet/books/tutorial.pdf (дата обращения 10.10.2014).
отправлен участнику


Оставить комментарий