ПРОЦЕСС  ТЕПЛОПРОВОДНОСТИ  В  ТВЁРДЫХ  ТЕЛАХ.  ТЕМПЕРАТУРНЫЕ  ПОЛЯ

Джамалов  Адиль  Чубанович

студент  3  курса,  кафедра  управления  в  технических  и  биомедицинских  системах,  СКФУ,  филиал,  РФ,  г.  Пятигорск

E -mail:  popeye125544@mail.ru

Пирмагомедов  Олег  Владимирович

студент  3  курса,  кафедра  управления  в  технических  и  биомедицинских  системах,  СКФУ,  филиал,  РФ,  г.  Пятигорск

E -mail:  popeye125544@mail.ru

Ткаченко  Роман  Михайлович

научный  руководитель,  канд.  физ.-мат.  наук,  СКФУ,  филиал,  РФ,  г.  Пятигорск

Известно,  что  тела  могут  проводить  тепло.  Если  один  из  концов  длинного  стержня  поместить  в  костер,  а  стержень  сделан  не  из  горючего  или  легко  плавящегося  материала,  то  другой  конец  через  некоторое  время  тоже  нагреется,  насколько  быстро  и  на  какую  температуру  —  зависит  от  материала,  размеров  стержня  и  других  факторов.  Процесс  теплопроводности  —  один  из  таких,  которую  называют  процессом  тепломассопереноса,  играющую  огромную  роль  в  природе  и  в  технике.  Другие  процессы  такого  рода  —  диффузия,  благодаря  которой  смешиваются  разные  жидкости  или  газы,  процессы  гидро-  и  аэродинамики  (т.  е.  переноса  (движения)  жидкостей  и  газов).

Между  ними  много  общего,  несмотря  на  то,  что  каждый  из  таких  процессов  имеет  собственные  закономерности.  Эти  процессы  происходят  в  сплошной  среде.  При  их  математическом  моделировании  используется  один  и  тот  же  математический  аппарат  —  дифференциальные  уравнения  в  частных  производных.  Параметры  многих  технологических  процессов  изменяются  не  только  во  времени,  но  и  в  пространстве,  в  качестве  примера  могут  служить  процессы,  связанные  с  термической  обработкой,  диффузией  и  т.  п.  (в  теории  управления  этот  класс  процессов  назван  системами  с  распределенными  параметрами  (СРП)).  К  числу  СРП  относится  широкий  круг  типичных  управляемых  объектов,  охватывающих,  в  частности,  как  традиционные,  так  и  новейшие  технологии  в  самых  различных  областях  техники,  зачастую  практически  не  реализуемые  с  требуемыми  качественными  показателями  без  построения  соответствующих  систем  автоматического  управления,  что  и  явилось  главным  стимулом  к  созданию  теории  и  методов  управления  СРП.  В  наше  время,  очень  часто  внедряется  разработка  различных  приложений  при  расчетах  математических  задач  численными  методами.  Это  связанно  с  простотой  обработки  информации  вводимых  данных  и  экономии  времени.  При  этом  как  правило  программы  становятся  универсальными  для  всех  дальнейших  задач  того  же  типа.  Компьютеры  делают  основные  операции  над  числами,  не  затрачивая  больших  временных  ресурсов.  Поэтому  сегодня  все  больше  времени  уделяется  средам  разработок  таких  программ  и  самое  важное  они  дают,  куда  большую  точность,  нежели  решение  таких  задач  аналитическим  способом. 

В  данной  работе  рассмотрено  построение  математической  модели  теплопроводности  пластины  с  конечными  размерами  [1,  с.  127].  Параметры  пластины  приведены  в  таблице  1.

Таблица  1.

Начальные  параметры  пластины

где:  Т  —  входное  воздействие  в  виде  заданной  температуры;

1  —  температура  поверхности  равна  0;

0  —  поверхность  теплоизолированная.

Задана  прямоугольная  пластина  c  линейными  размерами  и  величиной  входного  воздействия,  вычисляемым  по  формулам:

;

;

;

,  где  N  =2.

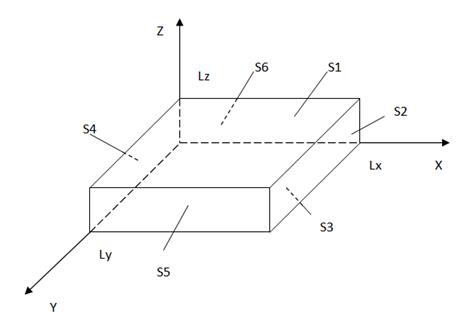
Рисунок  1.  Начальные  параметры  пластины

Математической  моделью  технологического  процесса  (объекта  управления)  называют  систему  математических  отношений  между  входными  и  выходными  параметрами  процесса  и  конструктивными  величинами,  показателями  качества,  а  также  ограничения,  накладываемые  на  параметры.

При  изучении  любого  физического  или  другого  какого-либо  явления  сначала  получают  качественное  описание  проблемы.  На  этапе  моделирования  качественное  представление  переходит  в  количественное.  Одновременно  определяют  функциональные  зависимости  между  переменными,  и  для  каждого  варианта  входных  данных  находят  выходные  данные  системы.

Для  перехода  от  содержательного  описания  к  математической  модели  необходимо:

1.  провести  декомпозицию  объекта,  разделив  его  на  элементарные  блоки,  узлы,  контуры,  процессы,  элементы  и  составить  структурную  схему  объекта;

2.  для  каждого  блока,  элемента,  контура  составить  уравнения,  описывающие  его  поведение  и  определить  математические  соотношения  между  параметрами  и  показателями  процесса;

3.  записать  все  математические  соотношения  между  элементами  системы  управления.

Для  математического  описания  процессов,  происходящих  в  объекте  необходимо  использовать:

·     уравнения  материального,  теплового  и  энергетического  баланса  с  учетом  гидродинамики  потоков  и  физических  свойств  жидкостей;

·     ограничения  на  параметры  процесса.

При  построении  математической  модели  используются:

1.  алгебраические  уравнения  для  описания  статических,  стационарных,  режимов  работы;

2.  обыкновенные  дифференциальные  уравнения  для  описания  динамических  объектов  с  сосредоточенными  параметрами  или  с  распределенными  параметрами;

3.  дифференциальные  уравнения  в  частных  производных  в  случае  описания  статических  моделей  объектов  с  распределенными  параметрами  по  нескольким  координатам  или  для  описания  динамических  нестационарных  процессов  объектов  с  распределенными  параметрами  [2,  с.63].

Уравнение,  описывающее  процесс  распространения  температуры  в  пластине  запишем  в  виде 

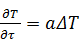  —  Общий  вид  уравнения  теплопроводности

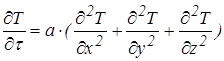  —  уравнение  теплопроводности  для  прямоугольной  системы  координат  (1)

где:  0  <x<L_x,  0  <y<L_y,  0  <z<L_z;  a  —  коэффициент  температуропроводности;

  —  температурное  поле  пластины; 

τ  —  время.

Запишем  граничные  условия:

Пластина  изготовлена  из  стали,  поэтому  для  неё  принимаем  следующие  значения:  коэффициент  температуропроводности  а  =  0,000019  м²/с.

Для  реализации  модели  проведем  дискретизацию  (рис.  2).  Разобьём  пластину  на  зоны  по  всем  трём  пространственным  координатам:

по  оси  X  с  шагом  дискретизации  ;

по  оси  Y  с  шагом  дискретизации  ;

по  оси  Z  с  шагом  дискретизации  . 

Шаг  дискретизации  по  времени  возьмём    с.

Определим  линейные  размеры  пластины:

L_x =  0,01*2  =  0,02  м,

L_y   =  0,02*0,4  =  0,008  м,

L_z   =  0,02*0,2  =  0,004  м.

Шаги  дискретизаций  высчитаем  по  формула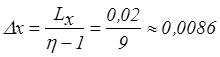м:

м,

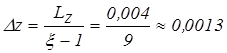м,

м.

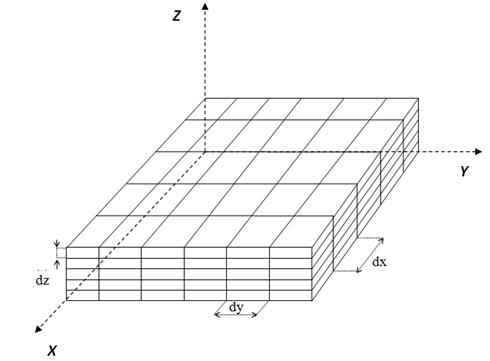
Рисунок  2.  Дискретная  модель  пластины

Входное  воздействие  в  виде  заданной  температуры  .  Тогда  получим

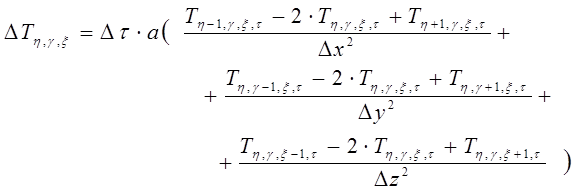         (2)

где—  разность  температур  в  соседних  точках  через  промежуток  времени  τ.

Температура  в  заданной  точке  вычисляется  по  формуле:

.

Учитывая  граничные  условия,  циклы  для  вычисления  температуры  по  всем  трём  пространственным  координатам  будут  иметь  вид:

по  оси  X;

по  оси  Y;

по  оси  Z.

График  изменения  температуры  для  точки  с  течением  времени  имеет  вид  (рис.  3):

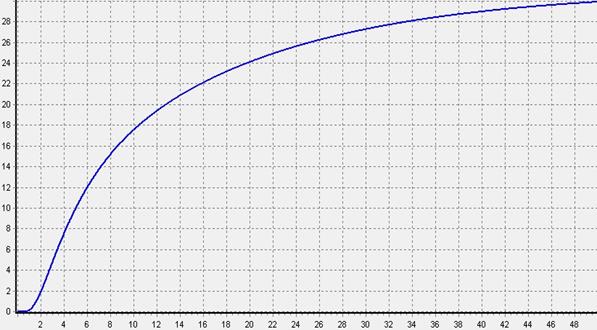
Рисунок  3.  График  изменения  температуры  пластины

В  ходе  работы  была  построена  математическая  модель  нестационарного  температурного  поля  внутри  пластины  заданных  размеров.  Для  вычисления  температурных  полей  можно  выбрать  императивный,  структурированный,  объектно-ориентированный  язык  Delphi,  и  среду  разработки  Embarcadero.

Список  литературы 

1.Базаров  И.П.  Термодинамика  /  М.:  Высшая  школа,  1983.  —  344  с.

2.Боглаев  Ю.П.  Вычислительная  математика  и  программирование  /  М.:  Высш.  Шк.,  1990.  —  544  с.

3.Першин  И.М  Системы  с  распределенными  параметрами.  Анализ  и  синтез.;  М.:  Научный  мир,  2012.  —  476  с.

4.Сухарев  М.В.  Основы  Delphi.  Профессиональный  подход;  М.:  Наука  и  техника,  2004.  —  600  c.