МОДЕЛИРОВАНИЕ  НАПРЯЖЕНИЙ  В  РЕЗИНОВОЙ  КАМЕРЕ  ГИДРАВЛИЧЕСКОГО  РУКАВА  С  ПОМОЩЬЮ  ТЕОРИИ  СИСТЕМ  С  РАСПРЕДЕЛЕННЫМИ  ПАРАМЕТРАМИ

Мерзлякова  Анна  Юрьевна

студент  4  курса,  кафедра  «Управление  и  информатика  в  технических

системах»  БИТТУ  (филиал)  СГТУ,  РФ,  г.  Балаково

E-mail:  anna 03.06.93@mail.ru

Мефедова  Юлия  Александровна

научный  руководитель,  канд.  техн.  наук,  доцент  БИТТУ,  РФ,  г.  Балаково

Теория  систем  с  распределенными  параметрами  предполагает  анализ  объектов  и  систем,  параметры  которых  зависят  не  только  от  времени,  но  и  от  пространственных  координат.  Поэтому  математические  модели  таких  объектов  представляют  собой,  как  правило,  дифференциальные  уравнения  в  частных  производных.  В  данной  работе  рассмотрен  пример  использования  данной  теории  для  моделирования  напряжений  в  резиновой  камере  гидравлическом  рукаве.  Данные  исследования  являются  начальными.  В  последствии  предполагается  исследовать  гидравлический  рукав  высокого  давления,  состоящий  из  нескольких  слоев  резиновой  камеры  и  металлических  оплеток,  решая  при  этом  контактную  задачу.

Рассмотрим  гидравлический  рукав,  используемый  в  качестве  гибкого  трубопровода  для  подачи  моторных  масел,  газов,  жидкостей,  топлива,  консистентных  смазок  под  давлением  в  агрегатах  различных  машин  и  оборудования.  В  процессе  работы  рукава  его  резиновые  и  металлические  слои  испытывают  механические  нагрузки  под  действием  силы  давления  транспортируемого  материала.  Смоделируем  задачу  распределения  механического  напряжения  во  внутренней  резиновой  камере  гидравлического  рукава.

В  качестве  моделируемого  рукава  примем  рукав  гидравлический  с  внутренним  диаметром  31,2  мм,  толщиной  внутренней  резиновой  камеры  1,4  мм  и  рабочим  давлением  20  МПа.  Материал  камеры  —  резина  плотностью  1200  кг/м³  и  с  коэффициентом  несжимаемости  0,00289  МПа^-1.  Особенностью  моделирования  будет  являться  тот  факт,  что  для  постановки  краевой  задачи  берется  произвольное  уравнение  из  справочника,  позволяющее  соблюсти  размерность  всех  входящих  величин.

Функция  Q(r,t)  (H/м²),  описывающая  распределение  механического  напряжения  в  резиновой  камере,  определяется  уравнением  [1,  c.  63]:

Данное  уравнение  одномерное  параболического  типа,  содержащее  первую  производную  по  времени.

Опишем  параметр  a,  входящий  в  данное  уравнение.  Для  получения  требуемой  размерности  данный  параметр  может  быть  рассчитан:

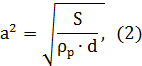
где:  S  —  площадь  поперечного  сечения  внутренней  камеры,  м²;

ρ_р  —  объемная  плотность  материала  внутренней  камеры,  кг/м³;

d  —  коэффициент  несжимаемости  материала  внутренней  камеры,  Па^-1.

Для  рукава  с  внутренним  диаметром  31,2  мм  и  толщиной  внутреннего  слоя  1,4  мм  площадь  поперечного  сечения  внутренней  камеры  составляет  6,504·10^-3  м².  Тогда  параметр  a:

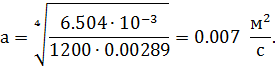
Так  как  механическое  напряжение  в  рукаве  в  начальный  момент  времени  отсутствует,  то  имеем  нулевые  начальные  условия:

Граничные  условия  представляются  в  виде:

·     при  воздействии  на  внутреннюю  поверхность  камеры  (r₀  =  0,156  м):

Примем  коэффициенты  ,  ,  рабочее  давление  внутри  резиновой  камеры    Па,  тогда  условие  (4)  примет  вид:

·     при  воздействии  на  внешнюю  поверхность  камеры  (r₁  =  0,163  м):

Примем  ,    и,  учитывая,  что  давление  на  внешнюю  поверхность  в  идеальном  случае  равно  нулю,  получим:

Для  выбранного  уравнения  параболического  типа  стандартизирующая  функция  имеет  вид  [1,  c.  64]:

С  учётом  принятых  начальных  (3)  и  граничных  (5),  (7)  условий  стандартизирующая  функция  (8)  принимает  вид:

Функция  Грина,  соответствующая  уравнению  (1)  [1,  c.  64]:

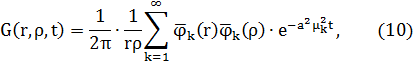
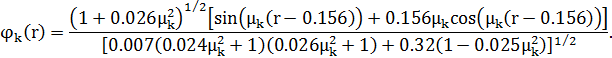
где  μ_k  —  расположенные  в  порядке  возрастания  положительные  корни  уравнения:

Преобразуем  данное  уравнение  с  учетом  вышеуказанных  условий:

Решая  его  графически  могут  быть  найдены  первые  положительные  корни.

Преобразованная  функция  Грина  примет  вид:

.

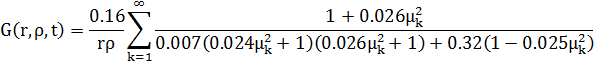
Идентификация  исходного  уравнения  позволяет  перейти  к  расчету  распределенной  выходной  величины,  являющейся  функцией  как  пространственной,  так  и  временной  координаты  и  рассчитываемой  как  пространственно-временная  композиция  от  произведения  функции  Грина  и  стандартизирующей  функции:

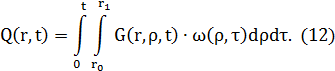
Решение  двойного  интеграла  (12)  имеет  вид:

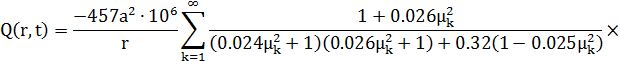
Ограничив  до  пяти  количество  корней  уравнения  (11)  получим,  что  последнее  выражение  для  расчета  выходной  распределенной  величины  при  a  =  0,007  м²/с  примет  вид:

Как  видно  из  последнего  выражения  выходная  распределенная  величина  является  функцией  двух  аргументов:  пространственной  координаты  r  и  временной  координаты  t.  Построим  график  этой  функции  при  фиксированном  времени  t  при  помощи  программы  MathCAD  (рисунок  1,  2).

Рисунок  1.  График  выходной  величины  Q(r,t)  при  t  =  1  с

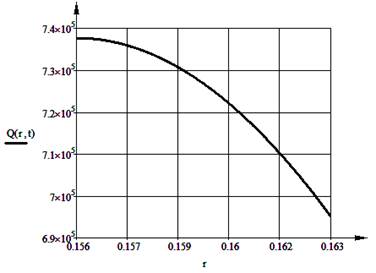
Рисунок  2.  График  выходной  величины  Q(r,t)  при  t  =  2  с

На  полученных  графиках  наблюдаем  монотонно  убывающую  в  пределах  от  внутреннего  (0,155  м)  до  внешнего  (0,163  м)  радиуса  резиновой  камеры  выходную  распределенную  величину  Q(r,t).  В  дальнейшем  планируется  исследовать  многослойную  конструкцию  рукава:  внутренняя  резиновая  камера,  металлическая  оплетка,  внешняя  резиновая  камера.  Для  этого  необходимо  решить  систему  из  трех  дифференциальных  уравнения  в  частных  производных.

Список  литературы:

1.Бутковский  А.Г.  Характеристики  систем  с  распределенными  параметрами.  М.:  Наука,  1979.  —  224  с.