ВЕЙВЛЕТ-АНАЛИЗ  СИГНАЛОВ  СИСТЕМ  С  ДИНАМИЧЕСКИМ  ХАОСОМ

Сергейчева  Анастасия  Николаевна

студент  5  курса,  кафедры  радиоэлектроники  и  квантовых  устройств  КНИТУ  им.  А.Н.  Туполева,  РФ,  Республика  Татарстан,  г.  Казань

E-mail:  anastasiya1703@bk.ru

Логинов  Сергей  Сергеевич

научный  руководитель  канд.  техн.  наук,  доцент,  КНИТУ  им.  А.Н.Туполева,  Институт  радиоэлектроники  и  телекоммуникаций,  кафедра  радиоэлектронных  и  квантовых  устройств,  РФ,  Республика  Татарстан,  г.  Казань

Вейвлеты  —  это  математические  функции,  позволяющие  анализировать  различные  частотные  компоненты  данных.  В  общем  случае  анализ  сигналов  производится  в  плоскости  вейвлет-коэффициентов  (масштаб-время-уровень),  которые  определяются  интегральным  преобразованием  сигнала  [9].  Вейвлет-спектрограммы  принципиально  отличаются  от  обычных  спектров  Фурье  тем,  что  дают  четкую  привязку  спектра  различных  особенностей  сигналов  ко  времени  [7].

На  сегодняшний  день  вейвлет-анализ  является  одной  из  самых  перспективных  технологий  анализа  данных,  его  инструменты  находят  применение  в  самых  различных  сферах  интеллектуальной  деятельности  [5].

Целью  данной  работы  является  исследование  вейвлет-спектров  нелинейных  систем  Лоренца,  Чуа,  Анищенко-Астахова,  Дмитриева-Кислова  с  динамическим  хаосом.

В  данной  работе  использовались  следующие  методы  спектрального  анализа:  дискретное  вейвлет  преобразование  и  непрерывное  вейвлет  преобразование.  Преимуществом  вейвлет-анализа  над  традиционными  методами  спектрального  анализа,  является  яркое  выделение  особенностей  сигнала  и  связь  спектральных  компонент  с  их  временным  расположением.  В  рамках  данной  работы  использованы  четыре  вида  вейвлетов:  Хаара,  Койфлеты,  Добеши  и  Биортогональные,  так  как  они  являются  ортогональными  и  имеют  компактный  носитель.

Проведен  спектральный  анализ  реализаций  нелинейных  систем  с  динамическим  хаосом,  выделены  особенности  спектров  их  сигналов.  Проанализированы  спектры  сигналов    переменных  систем  Лоренца,  Чуа,  Дмитриева-Кислова,  Анищенко-Астахова.  На  рисунке  1  в  качестве  примера  приведены  вейвлет-преобразования  непрерывного  и  дискретного  сигнала  системы  Дмитреева-Кислова.

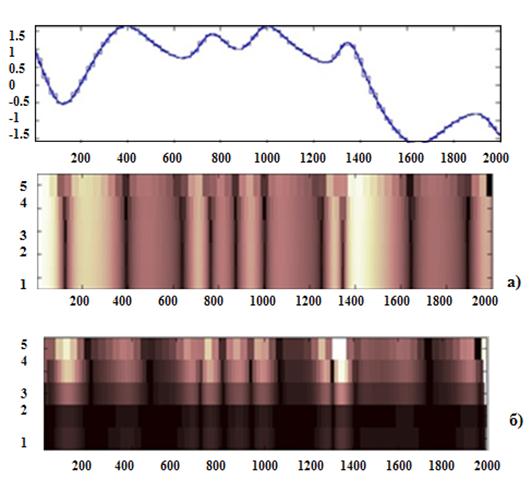
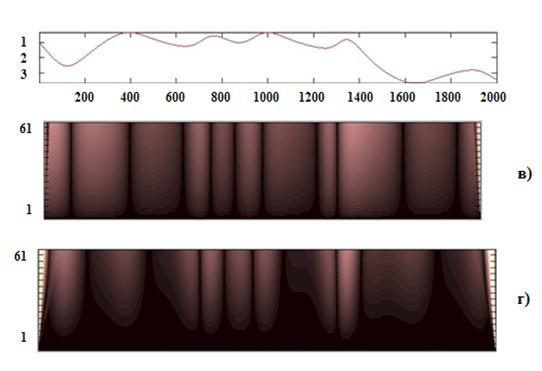
Рисунок  1.  спектры  сигналасистемы  Дмитреева-Кислова:  дискретное  вейвлет-преобразование  с  помощью  вейвлетов  а)  haar,  б)  coif  ;  непрерывное  вейвлет-преобразование  с  помощью  вейвлетов  а)  haar,  г)  coif

Ниже  представлена  таблица  характеристик  непрерывного  вейвлет  преобразования  системы  Дмитреева-Кислова  для  трех  ее  сигналов.

Таблица  1. 

Система  Дмитреева-Кислова

На  вейвлет-спектрограмме  вейвлета  haar  светлые  тона  соответствуют  изменение  амплитуды  сигнала,  а  темный  фон  постоянной  амплитуде.  У  вейвлета  coif  обратно  пропорциональное  изменение.  Показаны  пять  уровней  вейвлет-преобразований.  С  возрастанием  номера  уровня,  амплитуда  сигнала  уменьшается. 

На  подъеме  и  спаде  амплитуды  оттенки  будут  меняться  от  самого  светлого  до  темно-коричного  цвета.  Это  связанно  с  крутизной  фронтов.  Если  скорость  изменения  амплитуды  небольшая,  то  темный  оттенок,  если  же  большая,  то  светлее  оттенок.

На  полученных  спектрах  видны  характерные  частотные  компоненты  систем  с  нелинейной  динамикой.  Вейвлет-спектр  дает  более  подробную  информацию  о  характере  сигналов.  Таким  образом,  с  помощью  вейвлетов  можно  проводить  различные  операции  над  сигналами,  такие  как:  очистка  сигналов  от  шума,  сжатие  сигналов,  кратномасштабный  анализ,  выявление  точек  разрыва  и  характерных  особенностей  сигнала,  спектральный  анализ  и  выявление  долговременных  эволюций. 

Список  литературы:

1.Астафьева  Н.М.  Вейвлет-анализ:  основы  теории  и  примеры  применения  //УФН.  —  1996.  —  Т.  166.  —  №  11.  —  С.  1145—1170.

2.Дмитриев  А.С.,  Панас  А.И.  Динамический  хаос:  новые  носители  информации  для  систем  связи.  М.:  Изд.  физ.-мат.  лит.,  2002.

3.Дьяконов  В.П.  Вейвлеты.  От  теории  к  практике  М.:  СОЛОН-Р,  2002.

4.Карлов  Н.В.,  Кириченко  Н.А.  Колебания,  волны,  структуры.  М.:  физ.-мат.  лит.,  2003.

5.Киселев  Андрей  «Приложения  вейвлет-анализа».

6.Кузнецов  С.П.  Динамический  хаос.  М.:  Физ.-мат.  лит.,  2001.

7.Лоренц  Э.  Детерминированное  непериодическое  течение  //  Странные  аттракторы.  М.:  Мир,  1981.

8.Родионова  К.Ю.  «Использование  Вейвлет-преобразований  для  обработки  цифровых  сигналов».

9.Сонечкин  Д.М.,  Даценко  Н.М.,  Иващенко  Н.Н.  Оценка  тренда  глобального  потепления  с  помощью  вейвлетного  анализа  //  Изв.  РАН.  Физика  атмосферы  и  океана.  —  1997.  —  Т.  33.  —  №  2.  —  С.  184—194.

10.Сайт:  «Монографии  изданные  в  издательстве  Российской  Академии  Естествознания.» 

11.Хакен  Г.  Синергетика.  Иерархиии  неустойчивостей  в  самоорганизующихся  системах  и  устройствах.  М.:  Мир,  1985. 

12.Хакен  Г.  Информация  и  самоорганизация:  Макроскопический  подход  к  сложным  системам  /  Пер.  с  англ.  Ю.А.  Данилова.  М.  Мир,  1991.