«ПАРАБОЛИЧЕСКАЯ  ОМБИЛИКА»  ДЛЯ  ПОСТРОЕНИЯ  РОБАСТНО  УСТОЙЧИВОЙ  СИСТЕМЫ  УПРАВЛЕНИЯ  ТЕХНОЛОГИЧЕСКИМ  ПРОЦЕССОМ  СУШКИ

Ахметуллаев  Мершад  Аманжолович

студент  5  курса,  кафедра  КиИЛА  филиала  «Восход»  МАИ,  г.  Байконур

E -mail:  mershad@bk.ru

Кетебаев  Арман  Алдабергенович

студент  5  курса,  кафедра  КиИЛА  филиала  «Восход»  МАИ,  г.  Байконур

E-mail: 

Жуматаева  Жанат  Есиркеповна

научный  руководитель,  ст.  преподаватель  кафедры  ИТИиУ  филиала  «Восход»  МАИ ,  г.  Байконур

Проблема  робастности  в  настоящее  время  актуальна  применительно  к  системам  управления  объектами,  математическая  модель  которых  является  неполной  либо  содержит  неопределенности.

В  общем  смысле  робастность  подразумевает  устойчивость  к  внешним  воздействиям  в  условиях  неопределенности.  Если  выразить  робастность  посредством  понятия  чувствительности,  то  она  представится  как  низкая  чувствительность  запаса  устойчивости  к  изменению  параметров  объекта.

Робастными  называют  системы,  способные  сохранять  устойчивость  во  всем  диапазоне  изменений  параметров  в  результате  их  погрешностей,  условий  и  срока  эксплуатации. 

В  данной  работе  рассмотрено  построение  робастной  системы  управления  технологическим  процессом  сушки  в  классе  функций  катастроф  «параболическая  обмилика».  Математически,  процесс  можно  описать  в  виде:

,                                  (1.1)

где    —  коэффициент  усиления  объекта  управления,

  —  постоянная  времени, 

  —  температура  материала  (выходная  величина), 

  —  расход  топлива. 

Выражение  передаточной  функции  представляется  в  виде:

.                                        (1.2)

Предполагается,  что  процесс  сушки  состоит  из  одновременного  влияния  процесса  накопления  влаги,  определяющегося  скоростью  сушки  и  характером  теплового  объекта,  являющимся  инерционным  звеном  первого  порядка  (1.2)  [2,  с.  44—48].  Если  скорость  сушки  изменяется  по  закону  интеграла  ,  передаточная  функция  соответствующая  объекту  управления  выражается:

,

Образуется  система,  т.к.  к  уравнению  (1.1)  добавляется  новое  уравнение:

В  системах  управления  тепловыми  процессами  в  качестве  исполнительного  устройства  используется  интегрирующий  сервомеханизм  с  постоянной  интегрирования  . 

Система  автоматического  управления  с  пропорциональным  законом  управления    примет  вид

и  описывается  системой  дифференциальных  уравнений:

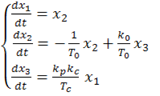                                      (1.3)

Применим  к  системе  закон  управления  в  форме  катастрофы  «параболическая  омбилика»,  чтобы  система  стала  робастно  устойчивой.

В  качестве  закона  управления  выберем

                            (1.4)

и  .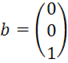

Таким  образом,  система  (1.3)  с  законом  управления  (1.4)  примет  вид:

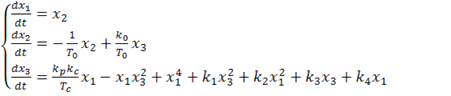        (1.5)

На  рисунке  1.1  изображена,  выполненная  в  среде  Vissim  6.0,  структурная  схема  системы  (1.5) 

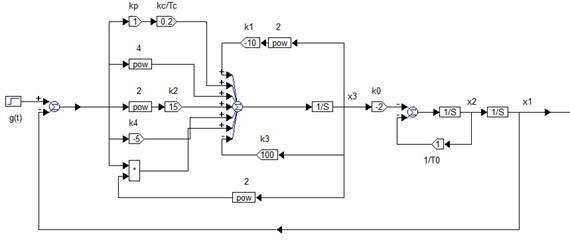
Рисунок  1.1.  Структурная  схема  системы

Исходя  из  этого,  система  (1.5)  характеризуется  следующими  стационарными  состояниями:

                                              (1.6)

,

где  , 

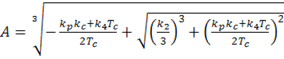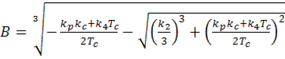  (1.7)

Представим  линеаризованную  систему  (1.5)  следующим  образом:

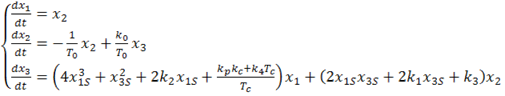    (1.8)

Система  (1.8)  при  стационарном  состоянии  (1.6)  имеет  вид:

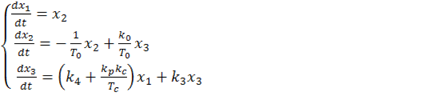  (1.9)

Система  (1.9)  выражается  следующим  характеристическим  уравнением:

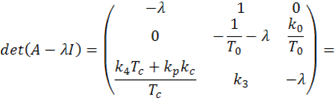
Характеристическому  уравнению  соответствует  матрица  Гурвица:

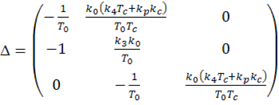
Учитывая  стационарное  состояние  (1.6)  выражаем  условие  устойчивости  для  системы  (1.8):

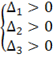  или         (1.10)

Так  как    и    положительные  для  того,  чтобы  выполнялись  системы  неравенств  (1.10)  достаточно,  чтобы  имело  место  выполнение  неравенства

                                     (1.11)

Система  (1.5)  становится  устойчивой  при  положительных  и  отрицательных  значениях    и  по  условию  (1.11)  при  любых  фиксированных  значениях  .

Численным  экспериментом,  проведенным  при  помощи  Vissim  6.0  подтверждается  то,  что  неустойчивая  в  одном  из  стационарных  состояний  (1.6)  и  (1.7)  система,  становится  устойчивой  в  другом,  и  наоборот,  что  представлено  на  рисунках  1.2-1.3,  при  следующих  значениях:

  .

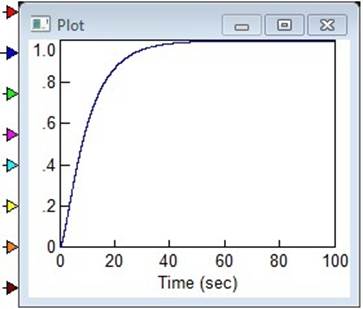
Рисунок  1.2.  График  устойчивости  системы  при  =2

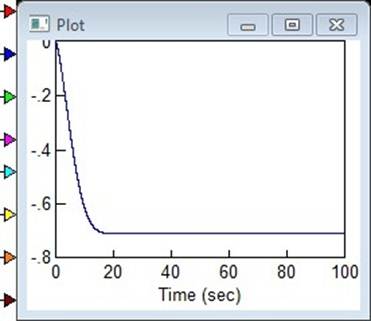
Рисунок  1.3.  График  устойчивости  системы  при  =-2

Применение  катастрофы  «параболическая  омбилика»  дает  гораздо  больше  вариантов  построения  робастно  устойчивой  системы  для  одного  и  того  же  объекта  управления,  в  данном  случае  —  для  технологического  процесса  сушки.  Основываясь  на  результатах  численного  эксперимента,  можно  утверждать,  что  примерно  при  одинаковых  основных  —    и    и  остальных  параметрах  объекта  использование  катастрофы  «параболическая  омбилика»  более  эффективно  по  качественным  показателям,  таким  как  колебательность,  время  переходного  процесса  и  перерегулирование  [3,  с.  59—66].

Практическое  использование  разработанных  методов  анализа  и  синтеза  систем  управления  в  классе  функций  катастроф  «параболическая  омбилика»  для  построения  САУ  технологическим  процессом  сушки  показало,  что  неустойчивая  система  управления  при  любом  линейном  законе  управления  не  только  стабилизируется,  но  и  не  имеет  ограничений  на  изменение  параметров  процесса  сушки.  В  сравнении  с  однопараметрическими  и  двухпараметрическими  структурно-устойчивыми  отображениями  здесь  появляется  значительно  больше  способов  построения  и  визуально  повышается  качество  управления.  Все  это  подтверждает:

·эффективность  и  справедливость  предложенного  подхода  построения  систем  управления  в  классе  функций  катастроф  «параболическая  омбилика»;

·справедливость  теоретических  положений  об  увеличении  потенциала  робастной  устойчивости  САУ  линейными  динамическими  объектами  в  классе  функций  катастроф  «параболическая  омбилика».

Список  литературы:

1.Бейсенби  М.А.  Модели,  методы  анализа  и  синтеза  предельно  устойчивых  систем  управления.  Автореф.  дис.  док.  Алматы  1998,  —  46  с.

2.Бейсенби  М.А.,  Ержанов  Б.А.  Системы  управления  с  повышенным  потенциалом  робастной  устойчивости.  Астана,  2002  —  164  с.

3.Жуматаева  Ж.Е.,  Бейсенби  М.А.  Построение  сверхробастной  устойчивой  системы  управления.  Вестник  МКТУ.  —  2009.  —  №  3(66).  —  120  с.