РАЗРАБОТКА  МЕТОДИКИ  РАСЧЕТА  НЕСТАЦИОНАРНЫХ  ТЕПЛОВЫХ  ПРОЦЕССОВ  ПРИ  НЕСУНУСОИДАЛЬНЫХ  РЕЖИМАХ  СЭС

Киселёв  Богдан  Юрьевич

студент  3  курса,  кафедра  электроснабжение  промышленных  предприятий  ОмГТУ,  РФ,  г.  Омск

E-mail :  bob_93_kz@mail.ru

Ширяев  Александр  Сергеевич

студент  4  курса,  кафедра  электроснабжение  промышленных  предприятий  ОмГТУ,  РФ,  г.  Омск

E-mail :  Alex2793@bk.ru

Иващенко  Александра  Валерьевна

студент  3  курса,  кафедра  электроснабжение  промышленных  предприятий  ОмГТУ,  РФ,  г.  Омск

E-mail :  ivashenko@mail.ru

Новикова  Светлана  Юрьевна

студент  3  курса,  кафедра  электроснабжение  промышленных  предприятий  ОмГТУ,  РФ,  г.  Омск

Е-mail: 

Осипов  Дмитрий  Сергеевич

научный  руководитель,  канд.  техн.  наук,  доцент  ОмГТУ,  РФ,  г.  Омск

Существующие  методики  расчета  уравнения  теплового  баланса  для  элементов  СЭС  относятся  к  случаю  стационарного  (установившегося)  теплового  режима.  Однако,  как  правило,  нагрузки  большинства  элементов  являются  резкопеременными  (суточные,  сезонные  изменения  нагрузок).  Вследствие  этого  возникает  задача  разработать  алгоритм  учета  фактического  нагрева  токоведущих  частей  при  расчете  несинусоидальных  режимов  СЭС  при  переменном  характере  нагрузок. 

В  данной  работе  приведены  методика  и  алгоритм  расчета  потерь  при  нестационарных  тепловых  процессах,  разработан  критерий  применимости  указанной  методики.  Проведенные  при  этом  исследования  показали,  что  неучет  изменения  графика  нагрузок  во  времени  при  расчете  тепловых  режимов  и  потерь  может  приводить  к  значительной  погрешности  (более  10  %).

1.  Уравнения  теплового  баланса  нестационарного  теплового  процесса  для  трансформаторов.

Распределение  потерь  по  элементам  сети  определяется  соотношениями  между  токами  и  активными  сопротивлениями  элементов  сети.  Если  элементы  сети  имеют  существенно  разные  загрузки,  то  независимо  от  условий  охлаждения  их  температуры  будут  различными.  Так  как  диапазон  изменения  температуры  проводника,  обусловленный  изменением  тока,  обычно  составляет  чуть  больше  половины  диапазона  его  рабочих  температур,  то  в  этом  диапазоне  сопротивление  может  изменяться  примерно  на  25  %,  а  отношение  сопротивлений  разных  элементов  -  соответственно  примерно  на  50%,  то  есть  неучет  нагрева  может  вызвать  погрешность  оценки  отношения  потерь  в  одном  элементе  к  потерям  в  другом  элементе  до  50%.

Производная  потерь  по  току  определяется  по  формуле:

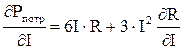.  (1)

Эта  формула  имеет  два  слагаемых,  первое  из  которых  при  изменении  температуры  меняется  в  тех  же  пределах,  что  и  сами  потери,  а  второе  меняется  от  нуля  при  малых  загрузках  до  некоторой  положительной  величины,  сравнимой  с  первым  слагаемым.  Это  значит,  что  диапазон  изменения  производной  потерь  при  изменении  температуры  больше,  чем  диапазон  изменения  потерь.  Из  этого,  а  также  из  соображений  по  поводу  распределения  потерь,  приведенных  выше,  следует,  что  неучет  температурной  зависимости  сопротивления  при  расчете  потерь  с  целью  выбора  мероприятий  по  их  снижению  может  привести  к  более  серьезным  ошибкам,  чем  при  расчете  потерь  без  указания  конкретной  цели.

Учтем,  что  ток  I  и  соответственно  полная  мощность  (нагрузка)  S,  а  также  температура  окружающей  среды  в  общем  случае  являются  функциями  времени,  и  введем  параметры  w  и  b,  значения  которых  определяются  по  формулам

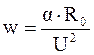,  (2)

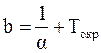,  (3)

где:  U  —  напряжение.

Тогда,  если  пренебречь  небольшими  изменениями  напряжения  во  времени,  средние  за  интервал  времени  от  t₁  до  t₂  потери  мощности  можно  записать  в  виде:

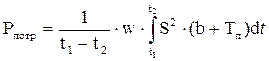.    4)

Перегрев  проводника  зависит  от  нагрузки  и  поэтому  тоже  является  функцией  времени,  причем  однозначной  связи  мгновенных  значений  нагрузки  и  температуры  в  связи  с  тепловой  инерционностью  элементов  сети  не  существует.  Можно  говорить  лишь  о  связи  зависимостей  перегрева  и  нагрузки  от  времени,  которая  задается  дифференциальными  уравнениями  нагрева  элемента  сети.  Если  пренебречь  скоростью  изменения  температуры  окружающей  среды,  то  в  простейшем  случае  имеем  одно  уравнение  нагрева:

,  (5)

где:  С  —  теплоемкость  элемента  сети; 

А_т  —  коэффициент  теплоотдачи 

Таким  образом,  потери  можно  определить  путем  решения  уравнения  (4)  и  интегрирования  (5).  В  общем  случае  это  можно  сделать  только  численными  методами. 

Уравнение  теплового  баланса  сухого  трансформатора  в  нестационарном  режиме  примет  вид: 

,  (6)

где:    —  теплоемкость  обмоток  трансформатора  [2].

В  качестве  численного  решения  исходного  дифференциального  уравнения  используем  метод  Рунге-Кутта  четвертого  порядка,  так  как  он  не  требует  вычисления  второй  производной  и  имеет  малую  погрешность.  Суть  которого,  состоит  в  нахождении  четырех  коэффициентов,  определяющих  приращение. 

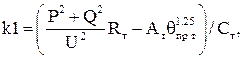  (7)

где:    —  первый  коэффициент,  характеризующий  приближение. 

На  следующем  этапе  к  температуре  обмоток    прибавляется  половина  значения  первого  коэффициента,  умноженного  на  шаг  (),  и  расчет  режима  начинается  заново.

  (8)

где:  h  —  шаг  сетки,  сек.;

Т  —  период,  на  котором  меняется  температура,  сек.;

n  —  число  шагов.

Экспериментально  установлено,  что  наиболее  приемлемым  для  данных  расчетов,  является  шаг  h=240  секунд.  В  нахождении  следующего  коэффициента  участвуют  уже  другие  величины.  Это  связано  с  тем  что  при  изменении  температуры  обмоток  изменяется  сопротивление  обмоток  трансформатора,  а  соответственно  изменяются  и  мощности.

Находим  второй  коэффициент.

.  (9)

Далее  к  температуре  обмоток    прибавляется  половина  значения,  но  уже  второго  коэффициента,  умноженного  на  шаг  ,  и  расчет  режима  начинается  заново.

,  (10)

При  нахождении  четвертого  коэффициента  к  температуре  обмоток    прибавляется  второй  коэффициент,  умноженный  на  шаг  .

  (11)

Новое  значение  температуры  находим  по  формуле:

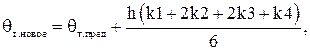  (12)

где:    —  новое  значение,  полученное  при  решении  производной;

  —  предыдущее  значение  температуры.

Задается  уровень  точности  .  Проверяется  —  проходит  ли  новое  значение  температуры  по  уровню  точности.  Для  этого  новая  температура  просчитывается  заново  по  формулам  (6—12),  но  уже  с  удвоенным  шагом  2h.  Находим  новое  значение  температуры.  Обозначим  его  как  .  Проверяется,  проходит  ли  новое  значение  по  уровню  точности. 

.  (13)

Если  выполняется  условие  (13),  то  продолжаем  вычисления    с  прежним  шагом,  если  нет,  то  делим  шаг  h=h/2  и  вычисления  начинаем  заново.

Цикл  повторяется  n  раз.  При  помощи  этого  метода  находится  ряд  значений  температуры.

В  зависимости  от  того,  нагревается  или  охлаждается  тело,  меняется  его  сопротивление,  а  значит  меняются  и  потери  в  нем. 

Список  литературы:

1.Гиршин  С.С.  Расчет  потерь  в  кабелях  с  учетом  нагрева  при  их  прокладке  в  земле.  Омск,  2001.  Деп.  в  ВИНИТИ  5.07.01,№  1609-В2001.

2.Гиршин  С.С.  Расчет  потерь  в  обмотках  силовых  масляных  трансформаторах  с  учетом  нагрева.  Омск,  2001.  Деп.  в  ВИНИТИ  5.07.01,№  1610-В2001.

3.Горюнов  В.Н.  Вопросы  моделирования  устройств  обеспечения  качества  электрической  энергии  /  А.Г.  Лютаревич,  В.Н.  Горюнов,  С.Ю.  Долингер,  К.В.  Хацевский//  Омский  научный  вестник.  —  2013.  —  №  1(117).  —  С.  168—173.

4.Горюнов  В.Н.  Расчет  потерь  мощности  от  влияния  высших  гармоник  /  В.Н.  Горюнов,  Д.С.  Осипов,  А.Г.  Лютаревич  //  Научные  проблемы  транспорта  Сибири  и  Дальнего  Востока.  —  2009.  —  №  2.  —  С.  268—273.

5.Осипов  Д.С.  Расчет  несинусоидальных  режимов  систем  электроснабжения  с  учетом  тепловых  процессов  в  элементах  сети.//  Динамика  систем,  механизмов  и  машин.  Сб.  материалов  международной  научно-практической  конференции.  Омск:  2004.  —  С.  257—260.

6.Осипов  Д.С.  Учет  фактического  нагрева  токоведущих  частей  при  расчете  потерь  в  сетях  промышленных  предприятий  с  нелинейной  нагрузкой.  Энергосбережение  и  энергетика  Омской  области  №  4  (13),  2004.

7.Основы  кабельной  техники.  Под  ред.  В.А.  Привезенцева.  Изд.  2-е,  перераб.  И  доп.  М.:  Энергия,  1975.  —  472  с.