ПАРАМЕТРИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  ВОЗМУЩАЮЩИХ  ВОЗДЕЙСТВИЙ  СИСТЕМЫ  СТАБИЛИЗАЦИИ  ПАРАМЕТРОВ  КАЧЕСТВА  LAN -КАБЕЛЯ

Головко  Валерия  Сергеевна

Федосеева  Светлана  Анатольевна

магистранты  1  курса,  кафедра  Автоматики  и  управления  в  технических  системах  СамГТУ,  РФ,  г.  Самара

E-mail: 

E-mail:  

Чостковский  Борис  Константинович

научный  руководитель,  д-р  техн.  наук,  профессор  СамГТУ,  РФ,  г.  Самара

В  настоящей  работе  рассматривается  задача  параметрического  моделирования  параметров  медной  жилы  с  пористой  изоляцией  —  диаметра  изоляции  и  погонной  емкости.  

Изолированная  жила  является  основой  двухпроводной  цепи,  в  данном  случае,  витой  пары  кабеля  передачи  данных  (LAN-кабеля).

Наложение  изоляции  методом  экструзии  является  наиболее  массовой  технологической  операцией  в  кабельной  промышленности.  Объектом  исследования  является  технологический  процесс  производства  LAN-кабелей.  Практически  все  экструзионные  линии  оснащены  датчиками  диаметра  изоляции  и  погонной  емкости,  используемыми  для  регулирования  степени  пористости  [5]. 

Цель  управления  —  автоматическая  стабилизация  диаметра  изоляции  и  степени  пористости.  Планируется  на  основе  полученной  параметрической  модели  обеспечить  оптимальные  настройки  регулятора  на  производственной  линии. 

Экспериментальные  данные  с  экструзионной  линии  TEL-35  при  изолировании  провода  TПппП-0,5-0,84  были  предоставлены  Самарской  Кабельной  компанией  (СКК). 

Реализации  измеренных  параметров  имеют  вид,  показанный  на  рис.  1.  Они  позволяют  построить  математическую  модель  и  осуществить  имитационное  моделирование  технологического  процесса  экструзии  пористой  изоляции  с  целью  оптимизации  параметров  законов  управления  данным  процессом.

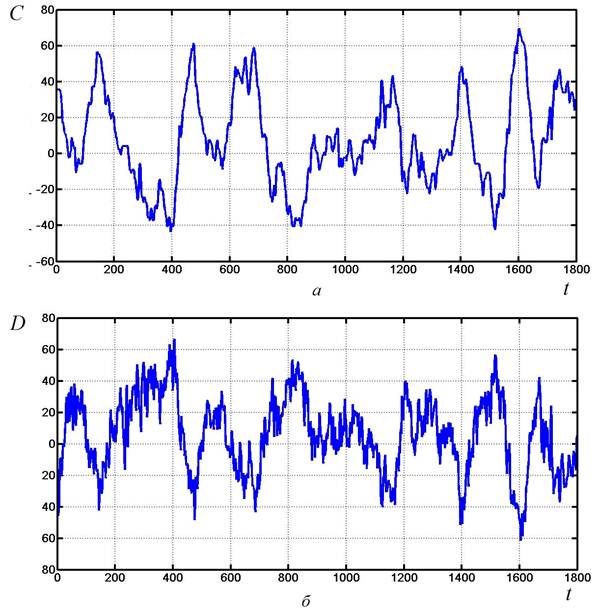
Рисунок  1.  Экспериментально  снятые  реализации :  а  —  погонная  емкость    изолированной  жилы;  б  —  диаметр  изоляции 

Эксплуатационные  характеристики  кабеля  (его  частотные  характеристики)  могут  быть  оценены  по  известным  функциям  спектральных  плотностей  частных  параметров  качества:  погонной  емкости  и  диаметра  изоляции.

В  [4]  на  основе  экспериментальных  данных  (рис.  1)  были  получены  оценки  спектральных  плотностей  и  корреляционных  функций  для  погонной  емкости  и  диаметра  изоляции  в  виде  числовых  массивов  (рис.  2,3),  которые  будут  использованы  для  построения  параметрической  модели.  Приведенные  характеристики  рассматриваются  в  относительных  величинах  для  наглядности  отображения.  Близость  данных  характеристик  позволяет  сделать  выводы  о  том,  что  вариации  погонной  емкости  в  основном  обусловлены  вариациями  диаметра  изоляции,  а  вариации  степени  пористости  изоляции,  определяющие  вариации  ее  диэлектрической  проницаемости,  малы.

Параметризация  необходима,  поскольку  непараметрические  оценки  корреляционно-спектральных  характеристик  стационарных  случайных  процессов  являются  бесконечномерными  моделями,  которые  неудобны  для  дальнейшего  использования  с  целью  синтеза  и  оптимизации  систем  управления  [3].

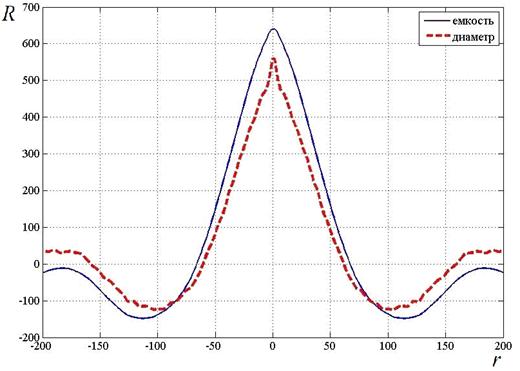
Рисунок  2.  Статистические  оценки  корреляционных  функций

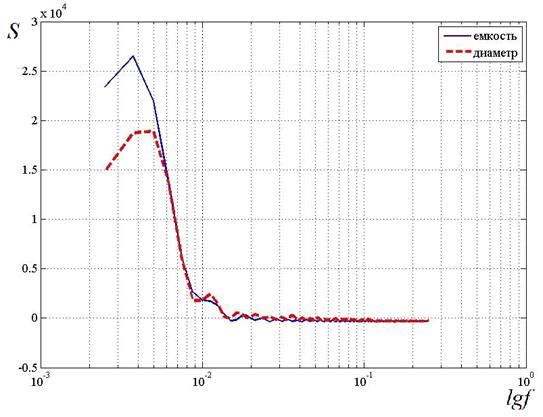
Рисунок  3.  Статистические  оценки  спектральных  плотностей

В  качестве  параметрической  модели  случайного  процесса  удобно  использовать  передаточную  функцию  формирующего  фильтра  [6].  Под  формирующим  фильтром  понимают  линейное  динамическое  звено,  выходной  сигнал  которого  имеет  заданные  корреляционно-спектральные  характеристики  при  поступлении  на  вход  фильтра  белого  шума  ,  т.  е.  случайного  процесса,  корреляционная  функция  которого  для  непрерывных  процессов  имеет  вид  :

`                                          (1)

где:  c  —  интенсивность  белого  шума; 

  —  единичный  импульс  (функция  Дирака).

Спектральная  плотность  белого  шума  постоянна  и  равна  интенсивности  с  на  всех  частотах  [1].

Наиболее  просто  задача  построения  формирующего  фильтра  решается,  если  моделируемый  случайный  процесс    описывается  одной  из  типовых  моделей  корреляционной  функции,  например,  экспоненциально  затухающей  или  имеющей  вид  экспоненциально  затухающей  косинусоиды  [6].

Простой  математической  моделью  описывается  случайный  процесс  на  выходе  звена  первого  порядка  (апериодического  звена)  при  поступлении  на  его  вход  белого  шума:

                                          (2)

Двухсторонняя  спектральная  плотность  данного  процесса:

=

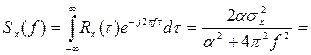
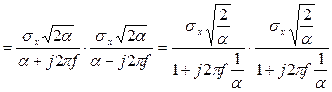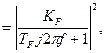                                     (3)

где:    и    —  параметры  формирующего  фильтра  первого  порядка,  постоянная  времени  которого  является  величиной,  обратной  коэффициенту  затухания  .

Если  корреляционная  функция  изучаемого  случайного  процесса  имеет  колебательный  характер,  то  обычно  она  описывается  в  виде:

                              (4)

Если  учесть,  что

,

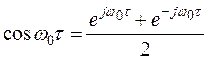спектральная  плотность  данного  процесса  получается  в  виде

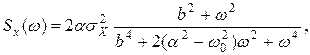               (5)

где:  , 

  —  коэффициент  затухания.

Рассмотрим  алгоритм  нахождения  аналитических  моделей  оценок  спектральных  плотностей  исследуемых  случайных  сигналов  [6].

По  корреляционной  функции  находится  период  колебательной  составляющей,  соответствующий  экстремуму  ее  правой  ветви  (рис.  2).  Расчет  коэффициента  затухания  осуществляется  по  формуле 

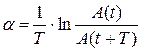,                                                (6)

где:    —  амплитудное  значение  корреляционной  функции  в  начале  периода, 

  —  в  конце  периода  [2].  Значение  корреляционной  функции  высчитывается  в  соответствии  с  дисперсией,  которая  равна  максимальному  значению  корреляционной  функции  [1].  Находятся  также  угловая  частота    и  параметр  .

С  учетом  полученных  расчетных  данных  получаем  параметрические  модели  оценок  спектральных  плотностей  емкости  (8)  и  диаметра  (9),  пользуясь  соотношением  (5).  Расчет  производился  с  использованием  пакета  MATLAB.

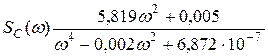.                               (8)

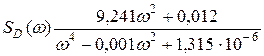                                  (9)

Убедимся  в  правильности  найденных  параметрических  моделей  (8),  (9),  сравнив  их  графики  с  графиками  оценок  спектральных  плотностей  на  основе  экспериментальных  данных  (рис.  4,5).  Можно  сделать  вывод,  что  полученные  модели  адекватны  ввиду  идентичности  экспериментальным  оценкам  спектральных  плотностей.

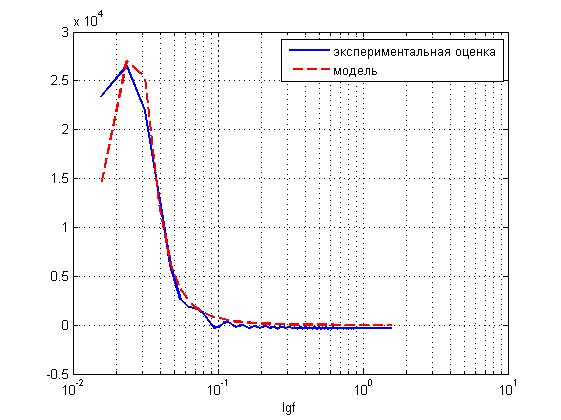
Рисунок  4.  Проверка  параметрической  модели  спектральной  плотности  погонной  емкости  на  адекватность

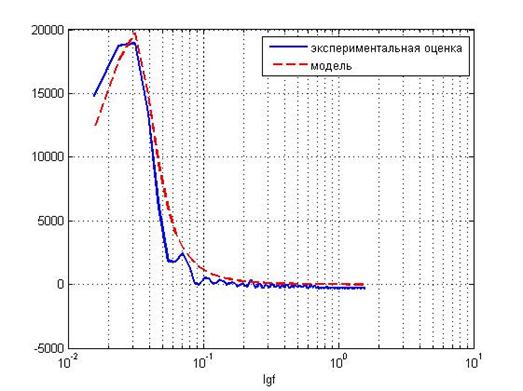
Рисунок  5.  Проверка  параметрической  модели  спектральной  плотности  диаметра  изоляции  на  адекватность

На  основе  полученных  параметрических  моделей  (8),  (9)  предполагается  нахождение  передаточных  функций  формирующих  фильтров  и  получение  окрашенных  шумов,  которые  должны  быть  идентичны  экспериментально  снятым  реализациям  (рис.  1). 

Параметрические  модели  возмущающих  воздействий  в  виде  формирующих  фильтров  будут  найдены  с  целью  синтеза  имитационной  модели  системы  стабилизации  параметров  качества  LAN-кабеля.

Список  литературы

1.Бендат  Д.,  Пирсол  А.  Прикладной  анализ  случайных  данных.  М:  Мир,  1989.  —  540  с.

2.Трофимова  Т.И.  Курс  физики:  учеб.  пособие  для  вузов.  М.:  Высшая  школа,  1990.  —  478  с.

3.Чостковский  Б.К.,  Волков  С.А.  Математические  методы  в  задачах  оптимизации  стохастических  систем:  учеб.  пособие.  Самара:  СамГТУ,  2007  —  72  с.

4.Чостковский  Б.К.,  Головко  В.С.  Статистическая  модель  процесса  изолирования  жилы  кабеля  передачи  данных  //  Вестник  Самарского  Государственного  Технического  университета.  Серия  «Технические  науки».  Самара:  СамГТУ,  —  2013.  —  №  2(38).  —  С.  33—41.

5.Чостковский  Б.К.  Методы  и  системы  оптимального  управления  технологическими  процессами  производства  кабелей  связи:  монография.  М.:  Машиностроение,  2009  —  190  с.

6.Чостковский  Б.К.  Моделирование  и  алгоритмизация  процессов  управления  в  стохастических  системах  с  цифровыми  регуляторами:  учеб.  пособие.  Самара:  СамГТУ,  2005  —  134  с.