РАСЧЕТ  МЕМБРАННО-ПНЕВМАТИЧЕСКИХ  СООРУЖЕНИЙ  С  УЧЁТОМ  НЕЛИНЕЙНЫХ  ФАКТОРОВ

Толеков  Мовлит  Абдулгафурович

студент  3  курса,  транспортное  строительство,  СГТУ  имени  Гагарина  Ю.А.,  РФ,  г.  Саратов

E-mail :  movlit_tolekov@rambler.ru

Ким  Алексей  Юрьевич

научный  руководитель,  д-р  техн.  наук,  профессор,  САДИ,  СГТУ  имени  Гагарина  Ю.А.,  РФ,  г.  Саратов

Статья  посвящена  ознакомлению  специалистов  с  разработанной  автором  новой  методикой  расчета  мембранно-пневматических  сооружений  с  учетом  нелинейных  факторов,  позволяющей  учесть  упругие  свойства  воздуха  в  пневмополостях.

Автором  статьи  совместно  со  своим  научным  руководителем  профессором  кафедры  ТСК  Кимом  А.Ю.  принимал  участие  в  разработке  ряда  воздухоопорных  (рис.  1)  и  линзообразных  мембранно-пневматических  сооружений  спортивного  назначения,  обладающих  высокими  технико-экономическими  показателями  [1,  2,  3,  4,  5,  6]

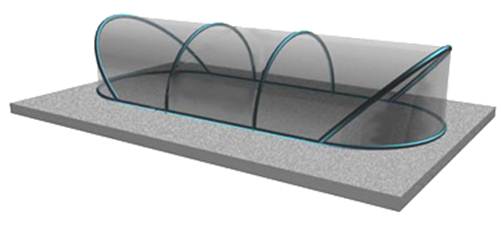
Рисунок  1.  Мембранно-каркасное  пневматическое  сооружение

Учитывая  экономический  кризис,  который  охватил  весь  мир,  разработка  новых  видов  пневматических  сооружений  и  их  разновидности  линзообразных  сооружений,  которые  характеризуются  экономической  эффективностью  по  сравнению  с  традиционными,  являются  очень  актуальными. 

Со  дня  своего  появления  в  1949  году  пневматические  сооружения  получили  большое  развитие  как  складские,  спортивные,  а  также  предназначенные  для  нужд  МЧС  и  госпиталей.  В  настоящее  время  таких  сооружений  на  всех  континентах,  включая  Антарктиду.  Развитие  строительства  с  учетом  современных  достижений  требует  повышения  эффективности  сооружений  при  экономии  затрат  за  счёт  внедрения  прогрессивных  конструкций  и  улучшения  эксплуатационных  качеств.

Мембранно-пневматические  системы,  как  показал  международный  опыт  строительства  сооружений  в  течение  последних  десятилетий,  относятся  к  прогрессивным  конструкциям.  Это  облегчённые  большепролетные  системы  сооружений,  которые  всё  чаще  возводятся  в  мире.  Теория  расчета  таких  сооружений  находится  ещё  в  стадии  разработки.

Современное  пневматическое  сооружение  обычно  содержит  воздухонагнетательный  вентилятор,  который  может  быть  совмещён  с  теплогенератором,  шлюзы  и  гибкую  оболочку,  образующую  полость  с  избыточным  давлением  воздуха  (рис.  2).

В  линзообразных  пневматических  покрытиях  сооружений  наличие  воздуходувной  машины  также  обязательно.  Обычно  это  работающий  от  щелочного  аккумулятора  центробежный  вентилятор,  который  служит  для  периодической  подкачки  воздуха  в  герметически  замкнутую  полость  покрытия.  В  отличие  от  воздухоопорных  сооружений,  в  которых  избыточное  давление  воздуха  создается  в  помещении  между  оболочкой  и  полом,  линзообразные  сооружения  не  требуют  герметизации  внутреннего  помещения  и  устройства  шлюзов.  Мембраны  покрытия  могут  быть  изготовлены  из  металла  или  из  синтетического  светопрозрачного  материала  [7].

Рисунок  2.  Интерьер  пневматического  сооружения  с  линзообразным  покрытием

Теория  расчета  мембранно-пневматических  систем  в  настоящее  время  разрабатывается  во  многих  странах  мира.  Разработке  методик  статического  и  динамического  расчета  мембранно-пневматических  систем  с  учётом  нелинейных  факторов  и  упругости  закаченного  в  замкнутую  полость  воздуха,  посвящены  многие  работы  многих  отечественных  исследователей  [2,  3,  4,  5,  6].  При  этом  автор  статьи  совместно  со  своим  научным  руководителем  применяет  для  расчета  метод  последовательных  приращений  параметров  с  поэтапным  применением  метода  конечных  элементов.

Метод  последовательных  приращений  параметров  с  поэтапным  применением  метода  конечных  элементов  позволяет  исследовать  на  ЭВМ  произвольные  мембранно-пневматические  системы  при  варьировании  различных  параметров.

Исследуемая  мембранно-пневматическая  система  может  содержать  шарнирно-стержневые,  балочные,  вантовые,  мембранные  и  другие  конечные  элементы  (рис.  3,  4).

На  конечной  монтажной  стадии  система  определена,  усилия  в  её  элементах  соответствуют  равновесному  состоянию,  система  обладает  достаточной  несущей  способностью.  На  стадии  эксплуатации  к  системе  могут  быть  приложены  пневматическая  нагрузка,  силовая  нагрузка,  температурное  воздействие  и  кинематическое  воздействие  в  любых  сочетаниях.

Рисунок  3.  Теплица  (Россия,  Ленинградская  область)

Рисунок  4.  Павильон  США  140  м  х  80  м  на  ЭКСПО-70  (Япония)

На  каждом  шаге  приращения  параметров  с  помощью  матрицы  связанности  узлов  формируется  исходная  система  поэтапно  линеаризованных  алгебраических  уравнений:

  ,  (1)

где:  r_ab  —  глобальная  матрица  жесткости  системы; 

h  —  матрица-столбец  искомых  перемещений; 

(  R_а  )  —  матрица-столбец  свободных  членов.

Порядок  матрицы  равен  ,  где  d  —  количество  заданных  опорных  связей  закрепленных  узлов  системы.

Каждый  элемент  матриц-столбцов  искомых  перемещений  h_b  и  свободных  членов  R_а  в  свою  очередь  состоит  из  подматриц-столбцов

  ,    ,  (2)

где:  u_nb,  v_nb,  w_nb  —  приращения  перемещений  узла  в  на  текущем  шаге  в  направлении  координатных  осей  х  ,у  и  z,  а  R_аx,  R_аy,  R_аz  —  реакции  в  наложенных  на  узел  а  связях  по  направлению  соответствующих  осей  от  заданного  нагрузочного  воздействия.

При  переходе  от  нумерации  узлов  к  глобальной  нумерации  наложенных  на  систему  связей  учитываем  зависимости:    ,  .

Индексам  ax,  ay  и  az  соответствуют  индексы  i,  i+1,  i+2,  а  индексам 

b_x,  b_y,  b_z  —  индексы  k,  k+1,  k+2. 

Вычислив  коэффициенты  системы  уравнений  (1)  при  а  =  1,  ,

в  соответствии  с  номерами  узлов  системы  формируем  разрешающую  систему  уравнений  метода  конечных  элементов

,  ,  (3)

в  соответствии  с  глобальной  нумерацией  наложенных  на  систему  связей.

Решая  систему  уравнений  (3),  находим  искомые  перемещения  x_k  и  распределяем  их  по  узлам  системы,  т.  е.  определяем  узловые  перемещения  u_na,  v_na  и  w_na  ,  полученные  системой  на  шаге  n  по  направлению  осей  х,  у  и  z.

Далее  определяем  приращение  продольного  усилия  DN_ab  в  каждом  стержне  аb  на  шаге  n.  Значения  координат  узлов  системы  x_a,  y_a,  z_a  в  конце  n-го  шага  варьирования  параметров  определяются  по  формулам

;  ;  .  (4)

При  расчете  мембранно-пневматических  систем  научный  руководитель  автора  статьи  предложил  учитывать  упругие  свойства  воздуха,  закаченного  в  герметически  замкнутую  полость  сооружения,  т.  е.  учитывать  влияние  на  давление  p_n  упругих  перемещений  поясов  линзообразного  покрытия.  При  этом  приращение  объема  пневмолинзы  DV  определяется  в  зависимости  от  давления  P  и  температуры  T  воздуха  в  замкнутой  полости  пневмолинзы.

Из  универсального  уравнения  состояния  газа

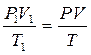    (5) 

объединяющего  известные  законы  Бойля-Мариотта  и  Гей-Люссака,  в  котором  параметры  P₁,  V₁,  T₁  характеризуют  систему  на  конечной  стадии  монтажа,  с  учетом  зависимостей

  ,  ,  ,

находим,  что

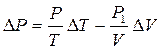,  (6)

Вычисляем  приращение  объема  DV  замкнутой  полости  в  зависимости  от  вертикальных  прогибов  поясов  покрытия  на  произвольном  шаге  n  нагружения  системы.

Полагая

,  ,  ,  ,  ,  ,  (7)

где  P^о  ,  V^о  ,  T^о  характеризуют  невозмущённое  состояние  системы  на  текущем  шаге  n,  т.  е.

,  ,

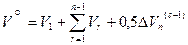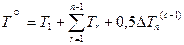,  (8)

выражаем  приращение  давления  в  замкнутой  полости  на  шаге  n  через  приращения  на  шаге  n  температуры  DT_n  и  объёма  DV_n  замкнутой  полости

  (9)

Список  литературы:

1.Ермолов  В.В.  Воздухоопорные  здания  и  сооружения.  М.:  Стройиздат,  1980.  —  304  с.

2.Ким  А.Ю.  Патент  РФ  №  2095534  от  10.11.1997  г.  Мембранно-каркасное  пневматическое  сооружение.  РОСПАТЕНТ  РФ,  Москва,  1997.  —  16  с.

3.Ким  А.Ю.  Расчет  мембранно-пневматических  систем  с  учетом  нелинейных  факторов.  Книга  1.  Континуальные  расчетные  схемы.  Саратовский  государственный  аграрный  университет,  Саратов,  2000.  —  198  с.  Монография  депонирована  в  ВИНИТИ  РАН  24.04.00  №  1148-В2000.

4.Ким  А.Ю.  Расчет  мембранно-пневматических  систем  с  учетом  нелинейных  факторов.  Книга  2.  Дискретные  расчетные  схемы.  СГАУ,  Саратов,  2000.  —  129  с.  Монография  депонирована  в  ВИНИТИ  РАН  29.05.00  №  1547-В2000.

5.Ким  А.Ю.  Численное  исследование  нелинейных  мембранно-пневматичес-ких  систем.  СГАУ,  Саратов,  2001.  —  263  с.  Монография  депонирована  в  ВИНИТИ  РАН  28.04.01  №  1122-В2001.

6. Ким  А.Ю.,  Нургазиев  Р.Б.  Расчёт  пространственных  мембранно-стержневых  систем.  СГАУ,  Саратов,  2001.  —  201  с.  Книга  депонирована  в  ВИНИТИ  РАН  31.08.01  №  1916-В2001.

7.Ким  А.Ю.  Статический  и  динамический  расчёт  воздухоопорных  и  линзообразных  мембранно-пневматических  систем.  Саратовский  государственный  аграрный  университет  им.  Н.И.  Вавилова.  Монография  деп.  в  ВИНИТИ  РАН  №  909  —  В2003  от  12.05.03.  —  308  с.