Статья опубликована в рамках: XVI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 21 января 2014 г.)
Наука: Технические науки
Секция: Машиностроение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ МОМЕНТА ИНЕРЦИИ ДЕТАЛИ АВТОКОЛЕБАТЕЛЬНЫМ МЕТОДОМ
Александрина Татьяна Александровна
студент 2 курса, кафедра технико-технологических дисциплин ВлГУ, РФ, г. Владимир
E-mail:
Шарыгин Лев Николаевич
научный руководитель, канд. техн. наук, профессор ВлГУ, РФ, г. Владимир
В студенческом конструкторском бюро «Хронос» при кафедре технико-технологических дисциплин ВлГУ выполнена разработка прибора для измерения моментов инерции тел [2] — рис. 1. Энергетические возможности измерительной автоколебательной системы прибора рассмотрены в статье Гильмановой И.Ф. этого сборника «Энергетические соотношения в измерительной автоколебательной системе инерциометра».

Рисунок 1. Внешний вид энерциометра
Обратимся к определению погрешностей измерения и диапазона измерения. Методика расчета погрешностей вытекает из процедуры измерения. Учитывая, что измеряемые детали могут иметь самую разнообразную форму, предварительно изготавливают и устанавливают на платформу (расположена в верхней части рис. 1) прибора крепежные элементы. После этого измеряют момент инерции измерительной автоколебательной системы ![]() через измерения периода колебаний
через измерения периода колебаний ![]()
![]() =
= ![]() . (1)
. (1)
Будем полагать, что линейная составляющая жесткости спиральной пружины C заранее определена с высокой точностью. Следующим шагом в процедуре определения искомого параметра ![]() является нахождение суммарного момента инерции нагруженной автоколебательной системы I через период колебаний
является нахождение суммарного момента инерции нагруженной автоколебательной системы I через период колебаний ![]() консервативной системы
консервативной системы
![]() =
= ![]() +
+ ![]() =
= ![]() (2)
(2)
Искомый параметр будет равен результату по формуле (2) за вычетом результата по формуле (1)
![]() = I -
= I - ![]() . (3)
. (3)
Из выражения (1) находим относительную погрешность определения собственного момента инерции ![]() в предположении, что погрешность определения жёсткости C значительно ниже погрешности определения периода
в предположении, что погрешность определения жёсткости C значительно ниже погрешности определения периода ![]() .
.
Так как
![]() ,
,
то
![]() = 2
= 2![]() , (4)
, (4)
где
![]() =
= ![]() и
и ![]() .
.
Аналогично выражению (4) относительная погрешность определения суммарного момента инерции I составит
![]() = 2
= 2![]() . (5)
. (5)
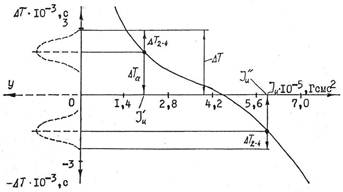
Рисунк 2. Графическая интерпретация погрешностей измерения
При вычитании двух приближенных величин — формула (3) — предельная абсолютная погрешность их разности ![]() равна сумме предельных абсолютных погрешностей уменьшаемого
равна сумме предельных абсолютных погрешностей уменьшаемого ![]() и вычитаемого
и вычитаемого ![]() [1]
[1]
![]() =
= ![]() +
+ ![]() (6)
(6)
или на основании выражений (4)—(6)
![]() = 2
= 2![]() + 2
+ 2![]() (
(![]() +
+ ![]() ) . (7)
) . (7)
Отсюда относительная погрешность величины ![]()
![]() = 2
= 2![]()
![]() + 2
+ 2![]() . (8)
. (8)
Для малых значений измеряемой величины ![]() , когда T
, когда T ![]()
![]() , можно принять
, можно принять ![]() , в этом случае формула (8) принимает вид
, в этом случае формула (8) принимает вид
![]() 2
2![]() . (9)
. (9)
При условии ![]() формула (8) принимает вид
формула (8) принимает вид
![]() = 2
= 2![]() . (10)
. (10)
Как показывают формулы (8)—(10) существенное значение на величину относительной погрешности измерения оказывает отношение ![]() . Необходимо при проектировании минимизировать собственный момент инерции системы
. Необходимо при проектировании минимизировать собственный момент инерции системы ![]() .
.
Формулы (8)—(10) получены в предположении свободных изохронных колебаний. В автоколебательном режиме система возбуждения вносит возмущения в колебательное движение, поэтому фактическое значение периода колебаний ![]() отличается от периода свободных изохронных колебаний T на величину
отличается от периода свободных изохронных колебаний T на величину
![]() =
= ![]() - T . (11)
- T . (11)
В теории автоколебаний отношение, ![]() называется относительным приращением периода. Эта величина определяется через производную фазы
называется относительным приращением периода. Эта величина определяется через производную фазы ![]()
![]() =
= ![]() = -
= - ![]() (12)
(12)
(формулу для ![]() см. в вышеупомянутой статье по энергетическим соотношениям).
см. в вышеупомянутой статье по энергетическим соотношениям).
Кроме систематической погрешности (12) имеются случайные погрешности обусловленные конечной стабильностью периода ![]() (функция добротности колебательной системы)
(функция добротности колебательной системы) ![]() , погрешностью формирования временного интервала
, погрешностью формирования временного интервала ![]() , погрешностью измерения сформированного временного интервала
, погрешностью измерения сформированного временного интервала ![]() .
.
Указанные случайные погрешности определяются схемотехническим исполнением вторичного преобразования, носят независимый характер, их суммарное влияние следует определять квадратичным суммированием
![]() =
= ![]() . (13)
. (13)
Перечисленные погрешности графически иллюстрируются рис. 2. Графики построены для системы ![]() =
= ![]() , C = 0,0217 Гсм. При расчете погрешности (13) принято: временной измерительный интервал
, C = 0,0217 Гсм. При расчете погрешности (13) принято: временной измерительный интервал ![]() формируется из 32-х периодов колебаний; граничные импульсы временного интервала имеют крутизну
формируется из 32-х периодов колебаний; граничные импульсы временного интервала имеют крутизну ![]() = 1,5
= 1,5 ![]() мВ/с; стабильность порога срабатывания отсчетных каскадов S = 100 мВ; частота опорного генератора для измерения временного интервала
мВ/с; стабильность порога срабатывания отсчетных каскадов S = 100 мВ; частота опорного генератора для измерения временного интервала ![]() равна
равна ![]() = 5 кГц. Вычисления выполнены в системе СГС.
= 5 кГц. Вычисления выполнены в системе СГС.
Поучительно посмотреть как изменяется относительная стабильность частоты ![]() от амплитуды колебаний A. На рис. 3 зависимость 1 построена для фиксированной амплитуды A =
от амплитуды колебаний A. На рис. 3 зависимость 1 построена для фиксированной амплитуды A = ![]() . Зависимость 2 соответствует реальной амплитудной характеристике системы. Заметим, что при увеличении
. Зависимость 2 соответствует реальной амплитудной характеристике системы. Заметим, что при увеличении ![]() амплитуда автоколебаний падает. Отсюда вывод — измерительную автоколебательную систему следует строить со стабилизацией амплитуды.
амплитуда автоколебаний падает. Отсюда вывод — измерительную автоколебательную систему следует строить со стабилизацией амплитуды.
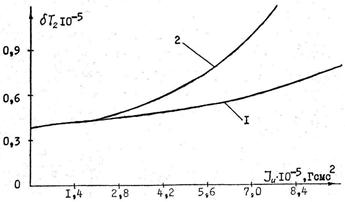
Рисунок 3. Относительная стабильность частоты: 1 — при фиксированной амплитуде колебаний (А=2700); 2 — при реальной амплитудной характеристике А = f(Iu)
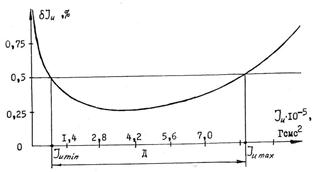
Рисунок 4. Графическое определение диапазона измерения
Вышеприведенные соотношения позволяют получить диапазон измерения Д. Для наглядности воспользуемся построением рис. 4. Функция погрешности ![]() = f(
= f(![]() ) построена по формуле (8). Задав допустимый уровень погрешности измерений в точках пересечения с функцией погрешности получим диапазон измерения Д, т. е. интервал изменения измеряемой величины, в пределах которого погрешность не превосходит заданной величины — интервал от
) построена по формуле (8). Задав допустимый уровень погрешности измерений в точках пересечения с функцией погрешности получим диапазон измерения Д, т. е. интервал изменения измеряемой величины, в пределах которого погрешность не превосходит заданной величины — интервал от ![]() до
до ![]() .
.
Таким образом, основными направлениями снижения погрешности измерения момента инерции детали автоколебательным методом являются:
· минимизация собственного момента инерции колебательного звена I0;
· повышение добротности колебательного звена за счет снижения потерь энергии на трение в подшипниках;
· стабилизация амплитуды автоколебаний.
Погрешности вторичного преобразования могут быть снижены современными электронными средствами.
Список литературы:
1.Демидович Б.П., Марон И.А. Основы вычислительной математики М.: Наука, 1970. — 463 с.
2.Устройство для измерения моментов инерции тсл. Патент RU86325, МПК G04C 3/00. / А.А. Бугров, А.В. Поваров, Л.Н. Шарыгин. Опубл. 27.08.2009. Бюл. № 24.
дипломов


Оставить комментарий