ПРОБЛЕМА  АВТОМАТИЧЕСКОГО  ПОИСКА  ИНВАРИАНТА  ЦИКЛА

Шипов  Андрей  Александрович

аспирант  1  курса  кафедры  информационной  безопасности  и  программной  инженерии  Российского  государственного  социального  университета,  РФ,  г.  Москва

E-mail: 

Кораблин  Юрий  Прокофьевич

научный  руководитель  д-р  техн.х  наук,  профессор,  профессор  кафедры  моделирования  информационных  систем  и  сетей  Российского  государственного  социального  университета,  РФ,  г.  Москва

Сегодня  программное  обеспечение  везде  вокруг  нас,  хотя  мы  его  и  не  видим.  Оно  присутствует  почти  в  любом  электронном  устройстве,  начиная  от  мобильных  телефонов  и  заканчивая  космическими  спутниками.  И  если  оттого,  что  в  нашем  телефоне  произойдет  какая-либо  программная  ошибка,  наши  страдания  в  большинстве  случаев  не  носят  трагический  характер,  то  если  что-то  случится  в  системе  реального  времени,  такой  как  самолет,  система  управления  атомной  станцией  или  система  противоракетной  обороны,  могут  возникнуть  человеческие  жертвы. 

В  современном  мире  почти  каждый  программный  продукт  содержит  в  себе,  хотя  бы  одну  ошибку.  И  с  этой  проблемой  хорошо  знаком  любой  программист,  хотя  бы  раз,  разрабатывавший  достаточно  сложную  программу.  Избежать  ошибок  во  время  разработки  и  кодирования  практически  невозможно.  А  если  еще  принять  во  внимание  то,  что  с  каждым  годом  программные  продукты  становятся  все  более  сложными  и  масштабными,  то  становится,  очевидно,  что  верификация  программ  является  одной  из  самых  сложных  и  серьезных  проблем  в  данной  области. 

Для  того  чтобы  не  допустить  сбоев  и  ошибок  в  программном  обеспечении  существуют  методы  верификации  программного  обеспечения,  которые  позволяют  доказать  правильность  работы  программы.

В  теории  верификации  программного  обеспечения  есть  необходимость  решения  трех  следующих  задач:

1.  Доказательство  частичной  корректности  выполнения  программ.

2.  Доказательство  завершимости  программ.

3.  Доказательство  незавершимости  программ.

Разработанный  Хоаром  [1;  2,  с.  15]  аксиоматический  подход  для  задания  формальной  семантики  программ,  является  одним  из  наиболее  широко  используемых  методов  решения  указанных  проблем.

Однако  ни  одна  из  этих  трех  задач  не  может  быть  в  полной  мере  решена  без  использования  инвариантов  цикла. 

Инвариантом  в  программировании  называется  логическое  выражение,  истинное  после  каждого  прохода  тела  цикла  (после  выполнения  фиксированного  оператора)  и  перед  началом  выполнения  цикла,  зависящее  от  переменных,  изменяющихся  в  теле  цикла. 

Однако,  поскольку  в  общем  виде  инвариант  цикла  не  является  очевидным  для  конкретного  цикла,  то  задача  о  поиске  инварианта  является  более  чем  актуальной  в  теории  верификации  программного  обеспечения.  Если  будет  возможным  найти  инвариант  для  любого  заданного  цикла,  то  это  позволит  в  большинстве  случаев  автоматизировать  процесс  верификации  программного  кода.  А  это  является  просто  чрезвычайно  важным  обстоятельством,  учитывая  сложность  и  размеры  большинства  современных  программ.

Одной  из  серьезных  проблем  в  теории  верификации  программного  обеспечения  является  проблема  завершимости  самой  программы.  Из  всех  существующих  программных  конструкций  только  циклические  конструкции  могут  привести  к  незавершимости  программ.  В  работе  [1,  с.  47]  предложены  условия  завершимости  циклов:

Р&B→(Е>O)  (1)

{0<E=E0}S{0≤E<E0}  (2)

Пусть  E  —  некоторое  целочисленное  выражение.  Предположим,  что  справедливо  условие  1  и  для  любого  выражения  Е0,  принимающего  целочисленные  значения,  справедливо  условие  2.  Это  означает,  что  утверждение  Е  ≥  0  также,  как  и  Р  является  инвариантом  цикла,  т.е.  выражение  E  остается  неотрицательным  в  течение  итерационного  процесса.  Кроме  того,  условие  (2)  означает,  что  каждое  выполнение  программы  C  уменьшает  значение  выражения  E.  Таким  образом,  из  справедливости  (1)  и  (2),  а  также  {Р  &  В}  C  {P}  непосредственно  следует  вывод  о  конечности  итерационного  процесса,  так  как  целочисленное  выражение  Е  не  может  уменьшаться  бесконечное  число  раз  и  оставаться  положительным,  как  требует  условие  (1).

Условия  завершимости  цикла  расширены  и  обобщены  в  работе  [4,  с.  6]:

"Eo$m({0<E=Eo}S^m{0£Е<Ео}),  (2*)

Таким  образом,  можно  сделать  вывод,  что  для  того  чтобы  доказать  завершимость  программы  необходимо  найти  утверждение  E  и  проверить  его  на  выполнение  условий  1  и  2*.

В  данной  работе  делается  попытка  найти  для  конкретно  заданного  цикла  инвариант,  который  позволял  бы  доказать  его  частичную  корректность.

Пусть  требуется  найти  инвариант  цикла  P,  который  позволял  бы  доказать  частичную  корректность  выполнения  некоторого  цикла.  Для  поиска  инварианта  P  мы  определим  некоторое  множество  операций  O  с  типичными  элементами  o,  с  индексами  или  без  и  множество  всех  переменных  V  также  с  типичными  элементами  x,  y,  z,…,  с  индексами  или  без,  входящих  в  структуру  инварианта,  а  именно  те  и  только  те  переменные,  что  изменяются  внутри  цикла.  Дополнительно  требуется  определить  множество  T  с  типичными  элементами  t,  с  индексами  или  без,  которые  будут  обозначать  некоторые  выражения.  Множество  T  будет  строиться  пошагово,  на  первом  шаге  все  элементы  множества  Т  полностью  совпадают  со  всеми  элементами  множества  V,  на  последующих  шагах  новые  элементы  множества  определяются  по  правилу  t_n  =  (t_i  o_k  t_j),  где  i  <  n,  j  <  n  и  i  ≠  j.

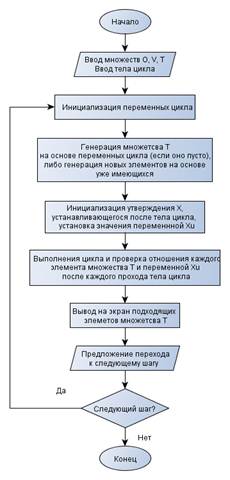
Рисунок  1.  Блок-схема  программы  для  поиска  инвариантов  циклов

Рассмотрим  все  сказанное  выше  на  конкретном  примере,  где  все  переменные  являются  целочисленными.

x  :=  x0;  z  :=  1;  n  :=  n0;

while  n  >  0  do  if  odd(n)  z  :=  z  _*  x;  fi

n  :=  n  /  2;  x  :=  x  _*  x;  od  {z  =  x0ⁿ⁰}

Найдем  инвариант  данного  цикла.  Вначале  определим  множество  всех  операций  O  =  {+,  –,  _*,  /,  ^},  состоящее  из  операций  сложения,  вычитания,  умножения,  деления  и  возведения  в  степень 

Далее  определим  множество  V  =  {x,  z,  n},  включающее  лишь  те  переменные,  которые  изменяются  в  теле  цикла. 

Далее  определим  элементы  множества  T  на  первом  шаге.  Поскольку  все  элементы  T  на  этом  шаге  полностью  совпадают  со  всеми  элементами  множества  V,  то  множество  T  =  {x,  z,  n}. 

Поскольку  программа  работает  с  конкретным  циклом  и  с  конкретными  значениями  переменных,  то  для  того,  чтобы  можно  было  проверить,  является  ли  конкретный  элемент  множества  T  искомым  инвариантом  P  нашего  цикла,  необходимо  задать  любые  значения  начальных  переменных  x0,  n0,  и  z0  и  выполнить  этот  цикл.  По  условию  примера  z0  =  1,  а  значит  остается  задать  только  значения  переменных  x0  и  n0.  Пусть  в  нашем  конкретном  случае  x0  =  2  и  n0  =  5.  Если  окажется,  что  несколько  элементов  множества  T  подходят  в  качестве  инварианта  P,  то  можно  будет  задать  новые  значения  переменным  x0  и  n0  и  повторить  поиск  инварианта  P.  Когда  мы  найдем  утверждение,  которое  возможно  является  искомым  инвариантом,  нужно  попытаться  доказать  с  его  помощью  частичную  корректность  данного  цикла.  Если  это  удастся  сделать,  то  данное  выражение  есть  инвариант  цикла.

Проверим  каждый  элемент  множества  T  на  необходимое  условие,  которым  является  следующее  утверждение:

Если  известно  некоторое  утверждение  X,  заданное  в  виде  некоторого  равенства  или  же  неравенства,  которое  устанавливается  после  выполнения  цикла,  то  его  можно  представить  в  виде  X  ≡  Xv  (*)  Xu.  Где  Xv  —  выражение,  состоящее  из  переменных  изменяющихся  в  теле  цикла,  а,  Xu  —  числовое  значение,  определяемое  начальными  переменными,  *  —  логическое  отношение  (равенство  или  неравенство).  Тогда,  искомый  инвариант  P  также  может  быть  представлен  в  виде  отношения  P  ≡  Pv  (*)  Pu,  где  Pv  —  некоторое  выражение,  Pu  —  значение  выражения,  *  —  логическое  отношение  (равенство  или  неравенство).  В  этом  случае  можно  утверждать,  что  Pu  =  Xu,  поскольку  и  инвариант  P  и  утверждение  X  установятся  после  выполнения  цикла,  также,  по  этому,  имеет  место  вхождение  переменных  выражения  Xv  в  выражение  Pv.

В  нашем  примере  утверждение  X  задано  в  виде  равенства  и  имеет  вид  z  =  x0ⁿ⁰.  Это  равенство  устанавливается  по  завершению  цикла  и  в  данном  случае  Xv  =  z,  а  Xu  =  x0ⁿ⁰.  Для  того,  чтобы  конкретный  элемент  множества  T,  в  данном  примере,  удовлетворил  заданному  условию,  его  значение  должно  быть  равно  x0ⁿ⁰.  Кроме  того,  каждый  элемент  множества  T,  претендующий  на  звание  инварианта,  обязательно  должен  содержать  в  себе  переменную  входящую  в  выражение  Xv,  а  именно  переменную  z.

Перейдем  к  следующему  шагу  и  дополним  множество  T,  которое  теперь  примет  вид:  T={x,  z,  n,  x  +  z,  x  +  n,…,  z  –  n,  n  –  x,…,x  /  z,  x  /  n,…,  n  ^  x,  n  ^  z}.

Посмотрим  результат  выполнения  программы  на  шаге  2:

Stage  2  invariants:  No  invariants  Next  stage?  (Y/N):

Нетрудно  заметить,  что  ни  один  элемент  множества  T  на  втором  шаге  не  удовлетворяет  нашему  условию.

Далее  перейдем  к  выполнению  шага  3.  Множество  T  теперь  примет  вид:  T=  {x,  z,  n,  x  +  z,  x  +  n,…,  z  –  n,  n  –  x,…,x  /  z,  x  /  n,…,  n  ^  x,  n  ^  z,  …,  (n  +  x)  –  (n  _*  z),  …,  (n  ^  x)  ^  (n  ^  z)}.

Проанализируем  результат  выполнения  программы  на  шаге  3:

Stage  3  invariants:  [[1],  '*',  [[0],  '**',  [2]]]  =  const

[[[0],  '**',  [2]],  '*',  [1]]  =  const  Next  stage?  (Y/N):

Соответственно,  результатом  работы  программы  являются  коммутативные  выражения  T_i  ≡  z  _*  xⁿ  и  T_j  ≡  xⁿ  _*  z  множества  T,  которые  и  являются  искомым  инвариантом  P  ≡  z  _*  xⁿ  =  x0ⁿ⁰  для  конкретного  цикла.

Для  доказательства  завершимости  программ  можно  использовать  разработанный  Хоаром  [1;  2,  с.  15]  аксиоматический  подход  для  задания  формальной  семантики  программ,  в  котором  операторы  языка  программирования  ассоциируются  с  отношениями  между  утверждениями. 

Выражение  E  является  утверждением,  для  которого  в  общем  случае  не  существует  алгоритма  поиска.  Чтобы  найти  выражение  E  и  попытаться  решить  данную  проблему  мы  используем  программу,  которая  будет  генерировать  множество  различных  выражений,  начиная  от  самых  простых  и  до  самых  сложных.  Будем  рассчитывать  на  то,  что  среди  них  окажется  хотя  бы  одно,  подходящее  в  качестве  искомого  выражения  E.

Для  поиска  Е  мы  определим  некоторое  множество  операций  O  =  {+,  –,  _*,  /,  ^},  состоящее  из  операций  сложения,  вычитания,  умножения,  деления  и  возведения  в  степень  и  определим  множество  всех  переменных  V  также  с  типичными  элементами,  входящих  в  структуру  инварианта,  а  именно  те  и  только  те  переменные,  что  изменяются  внутри  цикла.  Дополнительно  требуется  определить  множество  T,  состоящее  из  типичных  элементов,  которыми  будут  являться  некоторые  выражения. 

Множество  T  будет  строиться  пошагово,  на  первом  шаге  все  элементы  множества  Т  полностью  совпадают  со  всеми  элементами  множества  V,  на  последующих  шагах  новые  элементы  множества  определяются  по  правилу  t_n  =  (t_i  o_k  t_j),  где  i  <  n,  j  <  n  и  i  ≠  j.

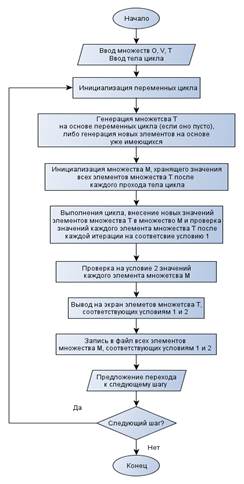
Рисунок  2.  Блок-схема  программы  для  поиска  выражения  E

Рассмотрим  конкретный  пример.

x  :=  100;  s  :=  -1;  n  =  0;

while  x  >  0  do  x  :=  x  +  s  *  n;  n  :=  n  +  20;  s  :=  -s;  od

Результатом  работы  программы:

Stage  1  result:  [0]

В  программе  переменные  для  данного  примера  заданы  в  виде  массива  m  =  [x,  s,  n],  поэтому  утверждением  E  в  данном  примере  является  переменная  x.  Поведение  переменной  x  приведено  на  рисунке  3.

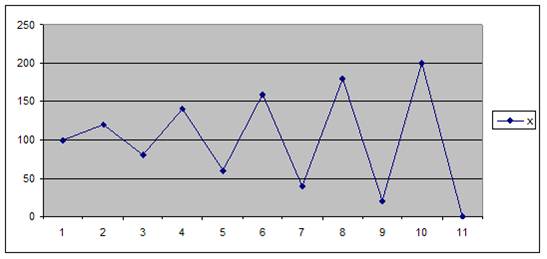
Рисунок  3.

Очевидно,  что  в  данном  примере  значение  переменной  х  уменьшается  за  прохождение  не  каждого  тела  цикла,  однако  все  же  оно  уменьшается  за  каждые  2  прохода  тела  цикла,  что  в  принципе  является  показателем  того,  что  оно  не  может  уменьшаться  бесконечным  и  оставаться  при  этом  положительным.

Предложенный  способ  поиска  инварианта  цикла  позволяет  во  многих  случаях  найти  утверждения,  которые  могут  рассматриваться  как  инварианты  циклов  для  использования  их  в  процессе  доказательства  частичной  корректности  программ.  А  предложенный  выше  способ  поиска  выражения  E  не  является  универсальным  и,  далеко  не  во  всех  случаях  позволяет  получить  необходимый  результат,  однако  он  существенно  расширяет  число  программ,  для  которых  становится  возможным  доказать  завершимость.  Это  позволяет  в  части  случаев  автоматизировать  сам  процесс  поиска  выражения  E,  процесс  доказательства  завершимости  программ  и  процесс  доказательства  частичной  корректности  программ.  Заметим,  что  поиск  инвариантов  сложных  циклов,  например  вложенных,  является  предметом  дальнейших  исследований  авторов.

Список  литературы:

1.Карпов  Ю.  Г..  Model  Checking.  Верификация  параллельных  и  распределенных  программных  систем.  Изд-во  БХВ-Петербург,  2010.  —  552  с.

2.Кораблин  Ю.П.,  Куликова  Н.Л.,  Логические  методы  доказательства  и  тестирования  программ.  Тезисы,  доклад  Международной  конференции  «Информационные  средства  и  технологии».  М.:  Международный  форум  информатизации  МФИ-96,  1996.

3.Кораблин  Ю.П..  Семантика  языков  программирования.  М.:  Изд-во  МЭИ,  1992.  —  100  с. 

4.Кораблин  Ю.П.,  Куликова  Н.Л.,  Чумакова  Е.В..  Семантические  методы  анализа  программ.  М.:  Изд-во  РГСУ,  2008  —  85  с.

5.ALAGIC,  SUAD;  ARBIB,  MICHAEL  A..  The  Design  of  Well-Structured  and  Correct  Programs.  New  York:  Springer,  1979.  —  292  с.

6.Hoare  C.A.R.  An  axiomatic  basis  for  computer  programming.  Northern  Irelan:  Queen's  Univ.  of  Belfast,  1969.  —  576—580  с.