Статья опубликована в рамках: XV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 24 декабря 2013 г.)
Наука: Информационные технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОД АДАПТИВНОГО РАСПРЕДЕЛЕНИЯ ТЕСТОВЫХ ВОПРОСОВ ПО ПРОВЕРЯЕМЫМ МОДУЛЯМ УЧЕБНОГО КУРСА
Леванов Дмитрий Николаевич
аспирант 3 курса кафедры моделирования информационных систем и сетей Российского государственного социального университета, РФ, г. Москва
E-mail: felis_pardus@mail.ru
Альтиментова Дина Юрьевна
научный руководитель старший преподаватель кафедры моделирования информационных систем и сетей Российского государственного социального университета, РФ, г. Москва
В статье описан метод, позволяющий компьютерной обучающей системе оптимально распределять общее количество тестовых вопросов по модулям тестируемого учебного материала
Рассмотрим учебную дисциплину, по которой информационные и тестовые материалы имеют модульную структуру. В этом случае текущую и итоговую проверку знаний студентов в общем случае можно представить в виде тестирования ряда модулей.
Компьютерная система, в отличие от традиционного преподавателя, в процессе тестирования может задать студенту сколь угодно большое число вопросов и оценить их правильность. Однако, исходя из нормативов учебного времени, общее число тестовых вопросов при проверке знаний должно быть ограниченно. Обозначим его через N. Величина его может варьироваться в зависимости от вида тестирования — учебное или контрольное.
Допустим, необходимо проверить знания по k модулям {M} = {M1, M2…, Mk}, по которым в системе имеется, соответственно, {N} = {N1, N2…, Nk} чисел тестов. Обозначим числа тестовых вопросов по разделам через {Q} = {Q1, Q2…, Qk}.
В общем случае при первом тестировании логично выбрать числа тестов {Q} пропорционально числам тестов {N}. Однако в случае повторной проверки знаний с учетом сохраненных результатов тестирования логичнее перераспределять число вопросов следующим образом: меньшее число вопросов задавать по тем модулям, по которым были показаны высокие результаты и большее число — по модулям с низкими результатами. Такой метод повторной проверки знаний модулирует действия реального преподавателя, который помнит предыдущие успехи тестируемого студента.
Предложен следующий алгоритм, практически реализующий предлагаемый метод.
Исходные данные:
1. общее число вопросов N,
2. модули M1, M2…, Mk , по которым производится тестирование,
3. числа N1, N2…, Nk , вопросов в модулях M1, M2…, Mk,
4. числа допущенных ошибок E1, E2…, Ek, вопросов в модулях M1, M2…, Mk, на предыдущем опросе, при первичном тестировании E1 = E2 =… = Ek = 1,
5. числа вопросов Qp1, Qp2…, Qpk в модулях M1, M2…, Mk, на предыдущем опросе.
Необходимо:
1. сформировать оптимальное распределение по модулям M1, M2…, Mk чисел тестов Qc1, Qc2…, Qck для текущего тестирования.
Основная идея метода — модули, по которым меньше ошибок, тестировать менее подробно, модули с большим числом ошибок тестировать более подробно.
Шаг 1. Расчет нормирующего коэффициента:
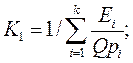
Шаг 2. Расчет долей вопросов по модулям:
![]()
Шаг 3. Расчет оптимальных чисел вопросов по модулям:
![]()
Пример применения метода.
Исходные данные:
1. общее число вопросов N = 12,
2. модули M1, M2…, M3 , по которым производится тестирование,
3. числа вопросов в модулях: N1=15, N2=22, N3=19,
4. числа допущенных ошибок при тестировании модулей E1=2, E2=3, E3=1,
5. числа тестов в модулях на предыдущем опросе Qp1=3, Qp2=5, Qp3=4.
Расчет:
Шаг 1. Расчет нормирующего коэффициента:
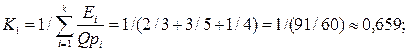
Шаг 2. Расчет долей вопросов по модулям:
![]()
![]()
![]()
Шаг 3. Расчет оптимальных чисел вопросов по модулям:
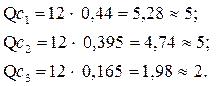
Рассмотренный метод позволяет автоматически регулировать распределение тестовых вопросов на этапе повторной проверки знаний по ряду учебных модулей учебного курса в зависимости от результатов предыдущих проверок, т. е. в адаптивном режиме. Его практическое применение должно стимулировать учащихся, поскольку студент, показавший неудовлетворительные результаты при промежуточном тестировании по какому-либо модулю учебного курса, будет знать, что при повторном тестировании обязательно будут присутствовать вопросы именно по этому модулю.
Переход на двухуровневую систему образования (бакалавриат — магистратура) стимулирует академическую мобильность, в связи с чем, возникает необходимость повышения конкурентоспособности учебных заведений на рынке образовательных услуг. Постоянное уменьшение доли аудиторной нагрузки в учебном процессе и увеличение часов для самостоятельной работы ставит на повестку дня разработку более эффективных компьютерных методов обучения и тестирования знаний. Внедрение новых разработок в области дистанционного обучения — один из основных показателей оценки успешности учебного заведения в современных условиях.
Проанализированы классические формы тестов, содержащих элементы адаптации:
1. гомогенные — тесты по конкретной дисциплине или разделу, система заданий возрастающей трудности,
2. гетерогенные — тест по нескольким учебным дисциплинам, система заданий возрастающей трудности,
3. интегративные — отличаются от гетерогенных большей информативностью каждого задания и меньшем числом заданий,
4. критериально-ориентированные — позволяют выявить, что из генеральной совокупности заданий учащийся знает и чего не знает, то есть какие разделы учебный дисциплины усвоены, а какие нет,
5. адаптивные тесты — предполагают подачу сложных заданий при правильных ответах пользователя на простые вопросы и простых заданий — если пользователь допускает ошибки.
Наиболее подходящими для компьютерной реализации являются адаптивные тесты. При использовании вместо преподавателя компьютера для повышения эффективности взаимодействия адаптивность таких систем должна быть существенно пересмотрена.
На основе проведенного анализа предложена формализация и математическое описание адаптивной модели одиночного альтернативного теста. Модель определяет более гибкий подход к процедуре оценки знаний обучающихся компьютерными системами.
Зависимость результата (R) от действий пользователя:
R=R({V}, N, {P}),
где: R — оценка тестового задания,
{V} — информация, полученная от ученика,
N — число вариантов ответа,
{P} — штрафные функции.
Анализ компонент предложенной зависимости:
R. Классический подход:

Предлагаемый подход:
RÎ[0,1].
V. Классический подход:
V ¹ Vист – ответ неверный,
V = Vист – ответ правильный.
Предлагаемый подход:
указывать несколько вариантов ответа.
Возможные варианты оценки:
Vист Î {V} верный ответ содержится в {V},
Vист Ï {V} верного ответа нет в {V}.
Вид зависимости R=R({V}, N, {P}):
R=R+({V}, N)×R-(N, {P}),
(R+) — положительная составляющая оценки,
(R-) — отрицательная (штрафная) составляющая оценки.
Виды зависимости R+:
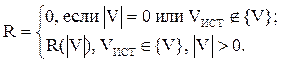
Линейная зависимость:

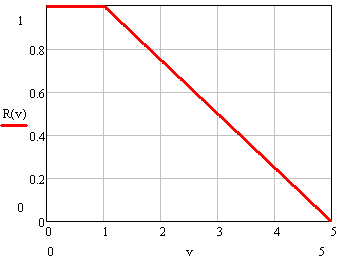
Рисунок 1. Линейная зависимость R+
Достоинства: простая. Недостатки: завышенные оценки при малых |V|, например при N=5 и |V| = 2 => R = 0.75.
Квадратичная зависимость:
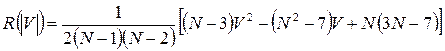
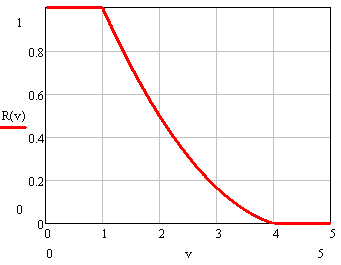
Рисунок 2. Квадратичная зависимость R+
Достоинства: ограничивает оценку при |V|>1. Недостатки: требует больших затрат на вычисление.
Виды зависимости R-:
Зависимость от времени ответа:
1) Tопт(N) = 5сек + N × 2сек;
2) {P} = T;
3) 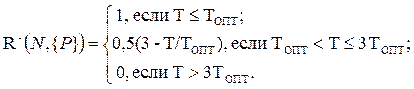

Рисунок 3. Зависимость R-
Время ответа зависит от трудоемкости тестового задания, поэтому Топт для каждого вопроса рассчитывается заранее.
Рассмотренная в статье модель одиночного альтернативного теста существенно повышает уровень адаптивности испытания за счет более полной оценки знаний пользователя, а также введения функций штрафа, например, за превышение времени ответа на вопрос.
дипломов


Оставить комментарий