ШУМОВЫЕ  ПРЕДЕЛЫ  ЧУВСТВИТЕЛЬНОСТИ  БИОСТРУКТУР  К  ЭМП

Ким  Александра  Валерьевна

аспирант,  кафедра  приборостроения,  ДВФУ,  г.  Владивосток

E -mail:  habibi89@bk.ru

Короченцев  Владимир  Иванович

научный  руководитель,  д-р  физ.-мат.  наук,  профессор,  ДВФУ,  г.  Владивосток

Один  из  феноменологических  подходов  к  определению  предельной  чувствительности  биосистем  к  ЭМП  постулирует,  что  биологический  детектор  ЭМП,  какой  бы  он  ни  был,  представим  в  виде  эквивалентной,  в  некотором  смысле,  электрической  цепи  или  радиотехнической  структуры,  состоящей  из  резисторов  и  емкостей.  Это  удобно,  так  как  собственные  электрические  шумы  легко  тогда  оценить,  используя  формулу  Найквиста.  Далее  утверждается,  что  предполагаемый  биологический  детектор,  не  располагая  априорной  информацией  о  детектируемом  сигнале,  способен  различить  лишь  сигнал  не  менее  собственного  шума.  Таким  образом,  оценка  чувствительности  биологической  системы  сводится  к  оценке  уровня  собственных  шумов  предполагаемого  детектора.

В  простейшем  случае,  биологическому  детектору  приписывается  комплексный  импеданс  Z(ω)  с  активным  сопротивлением  R  =(Z).  Тогда  спектральная  плотность  случайной  э.д.с.  равна:

.  (1)

В  данном  случае,  условия  справедливости  формулы  Найквиста  полагаются  выполненными:  ,  где    —  размер  детектора.  Считают,  что  биологические  ткани  и  биофизические  структуры  не  обладают  собственным  индуктивным  сопротивлением.  Наблюдаемая  иногда  в  измерениях  индуктивная  компонента  обусловлена  запаздыванием  тока  вследствие  включения  электрохимических  процессов  [1].  Поэтому,  реактивная  часть  импеданса  определяется  емкостным  сопротивлением,  обратно  пропорциональным  частоте,  (Z)=1/ωC.  Тогда  эффективная  полоса  частот  детектора  равна  ∆ω∼2π/RC.  Формула  Найквиста  дает  в  этой  полосе  средний  квадрат  шумовой  э.д.с.  детектора  2=4π/C.

Неоднократно  высказывалась  гипотеза,  что  молекулярной  мишенью  ЭМП  являются  ионные  каналы  биологических  мембран.  Мембраны,  образованные  фосфолипидами,  имеют  толщину  около  d  ≈  5·10⁻⁷см  и  диэлектрическую  проницаемость  порядка  ε  ≈  10.  Поскольку  емкость  участка  мембраны  с  радиусом  порядка  радиуса  ионного  канала  r  ≈  10⁻⁷  см  равна  C∼εr²/4d,  то  шумовая  э.д.с.,  отнесенная  к  толщине  мембраны,  то  есть,  шумовое  электрическое  поле  в  ионном  канале,  имеет  уровень:

.  (2)

Напомним,  что  поле,  индуцируемое  переменным  МП  50  Гц  100  мкТл  в  образце  размером  1  см  вблизи  оси  соленоида  равно  по  порядку  величины  0,1  мВ/м.  Также  зарегистрирована  реакция  биологических  систем  на  токи  в  тканях  инициируемые  полями  3—5мВ/м.  Таким  образом,  ограничения,  связанные  с  шумами  не  позволяют  одиночному  каналу  быть  рецептором  слабых  электрических  полей,  в  рамках  «радиотехнического»  представления. 

Формально,  обратно  пропорциональная  зависимость  E_noise  от  размера  r  участка  мембраны  позволяет  предполагать,  что  детектор  представленный  сравнительно  большим  участком,  был  бы  гораздо  чувствительнее.  Имеются  некоторые  соображения  о  том,  как  подобные  расчеты  могли  бы  быть  привязаны  к  оценке  чувствительности  гипотетического  детектора  слабого  электрического  поля  в  виде  большого  ансамбля  одиночных  каналов  или  в  виде  отдельной  клетки  [2].  Другое  направление  в  развитии  этой  темы  дает  работа  [3]  где  предположено,  что  ориентация  некоторых  пластиножаберных  рыб  в  геомагнитном  поле  обусловлена  э.д.с.,  наводимой  в  больших,  порядка  поперечного  размера  рыбы,  контурах  при  изменении  магнитного  потока  через  контур.  Электрорецепторы  рыб  обладают  высокой  чувствительностью  [32]  и  могли  бы  в  их  связи  с  электрическими  проводящими  контурами  объяснить  факт  магниторецепции.  По  данным  [3]  электрорецепторы  ската  обладают  сопротивлением  10⁵  Ом.  Положим,  что  характерная  частота,  связанная  с  движением  ската,  как  и  полоса  эффективных  частот  электрорецептора,  имеет  порядок  ω  =  10  Гц,  а  площадь  проводящего  контура  равна  S  =  10  см².  Тогда,  приравнивая  друг  к  другу  среднюю  шумовую  и  индуцированную  наклонами  контура  э.д.с.,  SωB/c,  легко  вывести  соотношение  для  пороговой  чувствительности  к  МП:

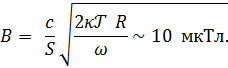
Эта  цифра  не  противоречит  гипотезе,  связывающей  магниторецепцию  этих  рыб  с  явлением  магнитной  индукции  и  электрорецепторами.  Также  она  не  противоречит  и  экспериментальным  данным  Калмийна  [5]. 

Несмотря  на  видимый  общий  характер  оценок,  область  их  применимости  ограничена  механизмами,  связанными  с  протеканием  тока  через  детектор  вследствие  дополнительной,  детерминированной  э.д.с.  сигнала.  Действительно,  если  бы  сигнал  модулировал  бы,  например,  только  собственное  сопротивление  детектора,  никакого  обнаружения  не  состоялось  бы.  Выпадают  из  этой  схемы  и  механизмы,  в  которых  под  действием  сигнала  меняется  скорость  химической  реакции:  никакого  электрического  аналога  этот  процесс  не  имеет.  Механизмы,  которые  обеспечивают  амплитудные  окна  эффективности  МП,  также  нельзя  анализировать  в  рамках  этого  подхода:  линейные  электрические  цепи,  даже  самые  сложные,  будучи  линейными  системами,  обладают  избирательными  свойствами  лишь  по  отношению  к  частоте,  но  не  к  амплитудам  сигналов.  С  другой  стороны,  введение  ad  hoc  в  эквивалентные  электрические  структуры  дополнительных  нелинейных  элементов  сделало  бы  невозможным  применение  формулы  Найквиста.  Флуктуационно-диссипационная  теорема,  лежащая  в  основе  формулы  Найквиста  ограничена  системами  с  линейным  откликом.

Отметим,  что  сама  возможность  представления  биологической  системы  в  виде  электрической  цепи  требует  обоснования.  Пилла,  Насер  и  Кауфман  [6]  предполагали,  что  биологическую  ткань  можно  изобразить  линейной  одномерной  цепью  электрически  связанных  одиночных  клеток,  каждая  из  которых  имеет  эквивалентную  электрическую  схему  из  резисторов.  Такая  цепь,  при  определенных  условиях,  позволяет  преодолеть  шумовой  предел,  начиная  с  полей  порядка  1  мВ/м.  Однако,  с  одной  стороны,  сведение  биологической  ткани  к  одномерной  цепи  не  совсем  убедительно.  С  другой  стороны,  эффекты  слабых  ЭП  наблюдают  и  на  уровне  клеточных  систем  вне  прямого  контакта  клеток.  Пока  нет  данных,  что  расчеты  предельной  чувствительности  в  рамках  данного  представления  согласовались  бы  не  с  числом,  а  с  экспериментальными  кривыми.  Барнс  [7]  предложил  рассматривать  нейроны,  пирамидальные  клетки  кортекса  головного  мозга  как  своеобразные  радиотехнические  антенные  фазированные  решетки,  снабженные  усилителями  и  фильтрами.  Такие  решетки  осуществляли  бы  детектирование  когерентных  сигналов,  наведенных  низкочастотными  внешними  полями  в  дендритах  нейронов  на  фоне  тепловых  шумов.  Однако,  способ  проверки  такой  гипотезы  не  был  предложен.  Таким  образом,  имеется  много  оснований  для  поиска  альтернативных,  несвязанных  с  электрическими  токами,  нелинейных  механизмов  биологической  рецепции  слабых  МП. 

Если  ограничиться  биологическими  эффектами  МП  уровня  геомагнитного  поля,  то  наиболее  важны  с  точки  зрения  фундаментальной  физики  две  проблемы  равно  парадоксального  характера:  1)  механизм  или  процесс  преобразования  сигнала  МП  в  биохимический  отклик,  масштаб  энергии    которого  на  десять  порядков  превосходит  квант  энергии  МП  и  2)  почему  тепловые  флуктуации  того  же  масштаба    не  разрушают  указанный  процесс  преобразования.  На  первый  взгляд,  парадоксальность  второй  проблемы  гораздо  более  заметна,  т.  к.  «очевидное»  решение  первой  состоит  в  накоплении  энергии  сигнала  МП  или  его  усилении.  Соответственно,  основное  внимание  уделялось  решению  второй  проблемы,  при  этом  механизм  преобразования  выбирался  почти  произвольно.  Однако  именно  от  механизма  преобразования  зависит  описание  «оконных»  полиэкстремальных  спектров,  наблюдаемых  в  эксперименте,  именно  им  определяется  предсказательность  модели.  Поэтому  на  сегодня  нет  предсказательных  моделей,  решающих  обе  проблемы  одновременно,  за  исключением,  может  быть  [8].  В  то  же  время,  появились  предсказательные  модели  [9,  10],  решающие  первую  проблему.  Это  существенный  этап,  характеризующий  состояние  теоретических  исследований  в  области  магнитобиологии.  Предсказательность  таких  моделей  означает,  что  биологические  эффекты  слабых  магнитных  полей,  как  важного  экологического  фактора,  становятся  прогнозируемыми. 

Рассмотрим  теперь  более  подробно  некоторые  из  часто  выдвигаемых  механизмов  МБЭ.  Критика  таких  работ  представляется  хотя  и  неблагодарной,  но  необходимой  деятельностью. 

  Существует  некоторая  терминологическая  неопределенность.  Под  «циклотронным  резонансом  в  магнитобиологии»  в  литературе  часто  понимают  несколько,  по  сути  разных,  моделей,  принадлежащих  Либову.  Кроме  того,  эти  модели  вспоминают  почти  всякий  раз,  когда  находят  МБЭ  на  циклотронной  частоте  Ω_c  МП,  упуская  из  вида,  что  данная  комбинация  констант  иона  имеет  отношение  не  только  к  циклотронному  резонансу,  но  и  к  ряду  других  эффектов.  С  другой  стороны,  судя  по  литературе,  «параметрический  резонанс  в  магнитобиологии»  связан  не  с  конкретным  именем,  а  со  спецификой  математических  уравнений,  —  и  поэтому  обращен  ко  множеству  моделей,  классических  и  квантовых,  с  и  без  потенциальных  сил  и  т.  д.  Все  же  мы  сохраняем  эту  терминологию,  отдавая  дань  сложившейся  литературной  традиции,  и  надеемся,  что  читатель  без  труда  идентифицирует  каждую  из  следующих  моделей  в  рамках  предложенной  выше  объективной  классификации. 

Рассмотрим  модели  биологического  действия  слабых  электрических  полей.

Один  из  возможных  сценариев  действия  низкочастотного  МП  на  биологическую  систему  состоит  в  том,  что  МП  индуцирует  в  ткани  переменное  электрическое  поле.  Оно,  в  свою  очередь,  вызывает  вихревые  токи  и  электрохимические  явления.  Частотно-  и  амплитудно-селективное  действие  внешних  слабых  переменных  ЭП  составляет  проблему  и  само  по  себе.  Для  описания  соответствующих  механизмов  используют  уравнения  химической  кинетики,  в  которых  константы  некоторых  реакций,  характерных  относительно  большим  изменением  электрического  дипольного  момента,  полагаются  зависящими  от  напряженности  ЭП.  Обычно,  при  оценке  действия  слабого  ЭП  на  клетку  исходят  из  дополнительного  потенциала  на  поверхности  клетки,  помещенной  в  ЭП.В  модельных  задачах  рассматривают  сферические  или  цилиндрические  диэлектрики,  помещенные  во  внешнее  поле.  Известно,  что  потенциал  ЭПE  в  сферической  системе,  совпадающей  с  центром  диэлектрического  шара  имеет  вид  φ=−Er(1−A/r³),  где  константа  A  определяется  из  условий  на  границе  шара.  На  поверхности  шара  радиуса  R,  или  цилиндра:

,  (1)

где:    —  диэлектрические  проницаемости  среды  и  моделируемого  объекта.  Так  как  обычно  ε∼80  и  ∼3,  то  для  дополнительного  потенциала  на  шаре  получаем  выражение:

φ  ≈  −1.5  ERcosθ,  (2)

которое  часто  используется  в  специальной  литературе,  см.,  например  [11].

Кроме  этого,  двухслойная  клеточная  мембрана  несет  большой  по  величине  заряд,  отрицательный  на  внутренней  мембране,  который  создает  трансмембранную  разность  потенциалов  Um∼70  мВ.  Она  обусловлена  действием  мембранных  насосов-ферментов,  проталкивающих  ионы  против  градиента  их  концентрации.  Дополнительная  разность  потенциалов  на  поверхности  клетки  в  противоположных  в  направлении  поля  точках  следует  из  (2)  и  равна  3ER.  Поскольку  проводимость  внутриклеточной  плазмы  велика  по  сравнению  с  проводимостью  мембраны,  полагают,  что  эта  разность  потенциалов  набегает  только  на  двух  противоположных  участках  мембраны,  и,  таким  образом,  дополнительное  ЭП  внутри  мембраны,  индуцированное  внешним  полем,  в  R/2d  раз  больше  внешнего.  С  одной  стороны  клетки  трансмембранный  потенциал  возрастает,  с  другой  уменьшается.  Относительная  величина  изменения,  как  нетрудно  посчитать,  для  клетки  размером  R∼10  мкм  в  поле  1  В/м  равна:

.  (3)

Малость  этой  величины  также  составляет  проблему  в  электромагнитобиологии.  Непонятно,  как  столь  малые  изменения  могут  менять  мембранные  процессы.

Рисунок  1.  Поля  и  поляризации  на  внешней  поверхности  мембраны.  Поверхностную  плотность  зарядов  образуют  сторонние  и  поляризационные  заряды

Ситуация  на  самом  деле  еще  более  драматична,  так  как  имеются  факты  биологической  рецепции  полей  порядка  1  мВ/м.  Кроме  того,  сама  формула  (3)  вряд  ли  правомерна  в  оценке  изменения  потенциала  полой  структуры,  так  как  получена  для  сплошного  диэлектрика.  Не  усложняя  дело  сферической  симметрией,  которая  в  данном  случае  привносит  в  результат  лишь  несущественный  коэффициент  порядка  единицы,  клетку  проще  смоделировать  прямоугольным  ящиком,  заполненным  цитоплазмой  с  диэлектрическими  свойствами  такими  как  у  межклеточного  раствора.  На  поверхности  мембраны  ящика  имеются  сторонние  заряды,  обеспеченные  белками-насосами,  а  также  заряды  вследствие  поляризации  внешним  электрическим  полем  E.  Поверхностная  плотность  индуцированных  полем  зарядов  равна  разности  поляризаций  среды  с  внутренней  и  внешней  стороны  поверхности  мембраны  (рис.  1):

σ(E)=Pⁱ−P.  (4)

Так  как  мы  рассматриваем  эффекты  поляризации  в  линейном  приближении,  то  поляризационную  плотность  зарядов  можно  найти,  положив  временно  отсутствие  сторонних  зарядов.  В  этом  случае  на  границе  диэлектриков  выполнено  соотношение  εE=εⁱEⁱ.  Используя  также  равенство  4πP=(ε−1)E  с  обеих  сторон  мембраны,  находим:

4πσ(E)  =  εⁱEⁱ  −  Eⁱ−  εE  +  E  =  (1−ε/εⁱ)E.  (5)

Поверхностная  плотность  зарядов  связана  с  трансмембранным  потенциалом  соотношением  плоского  конденсатора:

U_m(E)=4π[σ_s+σ(E)]d/εⁱ,  (6)

где  d∼5нм  -  толщина  бимембраны.  Отсюда  находим  изменение  δU_m(E)  трансмембранного  потенциала  по  отношению  к  его  значению  в  отсутствие  поля  U_m(0)  =U_m:

,  (7)

то  есть,  еще  на  два  порядка  меньше  чем  (3).

Соотношение  (2)  использовали,  например,  Астумиан,  Вивер  и  Эдейр  [2].  Они  предложили  гипотетический  механизм,  иллюстрирующий  действие  переменного  электрического  поля  на  биологическую  клетку.  Этот  механизм  не  обладает  ни  частотной,  ни  амплитудной  избирательностью.  Рассмотрим  все  же  саму  идею,  что  поможет  выяснить  перспективу  ее  использования.  Мембранные  каналы  клетки  могут  находиться  либо  в  открытом,  либо  в  закрытом  состоянии,  рис.  2.  Такая  точка  зрения  обоснована  экспериментальными  наблюдениями  дискретного  изменения  проводимости  одиночных  белковых  каналов.  В  термодинамическом  равновесии,  в  условиях  больцмановской  статистики,  отношение  вероятностей  канала  находиться  в  открытом  и  закрытом  состояниях  равно:

p  ≡  p_open/p_close  =  exp(−U/).  (8)

Если  внешнее  электрическое  поле  вызывает  изменение  разности  потенциалов  согласно  соотношению  U=U₀+δU,  то  отношение  вероятностей  можно  представить  в  виде  ряда  по  степеням  малого  параметра  x=δU/U₀.  С  учетом  обозначения  β=U₀/  имеем:

p(x)=e^βe^βx=p(0)  +(0)x+x²/2+...  (9)

Изменение  p  в  среднем  по  времени  связано,  очевидно,  только  с  квадратичным  по  x  членом:

.  (10)

Предположение  состояло  в  том,  что  отклонение  p  от  равновесного  значения  может  привести  к  росту  скорости  переноса  белком  молекул  оксидантов  внутрь  клетки  и  к  накоплению  вследствие  этого  повреждений  ДНК  в  течение  достаточно  длительного  времени.

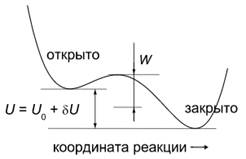
Рисунок  2.  Зависимость  свободной  энергии  белка-канала  от  обобщенной  координаты.  Устойчивыми  являются  открытое  и  закрытое  состояния

Величина  U₀  на  рис.  2  соответствует  трансмембранному  потенциалу  клетки  с  величиной  переносимого  заряда  в  несколько  единиц.  Тогда  δU  есть  изменение  этого  потенциала  во  внешнем  электрическом  поле.  Как  мы  определили  выше,  амплитуда  относительного  изменения  трансмембранного  потенциала  в  поле  1  В/м  равна  по  порядку  величины  10⁻⁶.  Поэтому  средняя  по  времени  величина  квадрата    есть 

∼10⁻¹²,  (11)

где  положено  x∼cosΩt. 

С  другой  стороны,  величинаβдля  физиологических  температур  приблизительно  равна  восьми.  Отсюда  получаем  оценку  постоянной  составляющей  в  изменении  величины  p  в  переменном  поле:

δp∼10⁻⁶–10⁻⁸.  (12)

Малость  этой  величины  указывает  на  сомнительность  использования  данной  идеи.  Согласно  расчетам  авторов  идеи,  указанный  уровень  переменного  поля  мог  бы  привести  к  биологическому  эффекту.  Однако  несколько  идеализаций,  сделанных  по  ходу  вычислений,  существенно  снижают  ценность  такого  вывода.  Предсказание  механизма  состоит  в  квадратичной  зависимости  эффекта  от  амплитуды  электрического  поля.  Механизм  действия  ЭП  на  биологические  системы,  клетки,  обладающий  частотной  избирательностью,  разрабатывался  в  цикле  работ,  обзор  которых  приведен  в  статье  Цонга  [12].  Идея  механизма  состоит  в  том,  что  если  конформационные  состояния  A  и  B  молекулы  обладают  дипольным  электрическим  моментом,  то  химическое  равновесие  этих  форм:  может  быть  смещено  во  внешнем  ЭП  E  в  соответствии  с  уравнением  типа  уравнения  Вант-Гоффа:

  [∂lnK/∂E]_P,V,T=∆M/R,  (13)

где:  K=k₁/k₋₁  —  константа  равновесия, 

M  —  разность  молярных  дипольных  электрических  моментов  состояний  A  и  B, 

R  –  газовая  постоянная. 

Это  применено  к  конформационным  состояниям,  активному  и  неактивному,  фермента  типа  АТФ-азы,  катализирующего  реакцию  мембранного  транспорта  субстрата  внутрь  клетки.  Частотная  избирательность  постулирована  и  является  следствием  соответствия  частоты  внешнего  поля  и  скоростей  релаксации  реагентов.  Амплитудной  избирательности  в  модели  нет,  хотя  обзор  экспериментов  по  АТФ-азным  реакциям  в  сильном  ЭП,∼0,5—5  кВ/м,  имеющийся  в  этой  статье,  показывает  наличие  максимума  в  районе  2  кВ/м.  Качественный  результат,  полученный  компьютерным  моделированием  при  некоторых  комбинациях  нескольких  параметров,  описывающих  ферментативный  транспорт  показывают,  что  ЭП  может  приводить  к  постоянной,  в  среднем,  прокачке  субстрата  через  мембрану.  Теоретических  оценок  величин  эффективных  полей  не  приведено.  Такая  оценка  следует  из  уравнения  (13),  переписанного  в  нормировке  на  одну  молекулу:

K/K₀  =  exp  (,  (14)

где  δD  —  разность  дипольных  моментов  молекулы  в  состояниях  A  и  B.  Иногда  эту  величину  связывают  с  перемещением  нескольких  элементарных  зарядов  на  расстояние  порядка  толщины  мембраны  d,  то  есть  δD∼10_ed.  Тогда,  при  физиологической  температуре,  в  поле  E∼1  кВ/м,  получим  δK/K₀∼10⁻³.  По-видимому,  следует  признать  перспективность  модели  в  объяснении  биологических  эффектов  сильных  электрических  полей.  Слабой  стороной  здесь  является  недостаточная  предсказательная  сила  модели,  сложность  ее  экспериментальной  верификации.  В  частности,  авторами  не  предсказаны  зависимости  эффекта  для  каких-либо  других  измененных  условий  электромагнитной  обстановки.

В  работе  [12]  предложен  еще  один  механизм  для  объяснения  биологической  рецепции  слабых,  порядка  мкВ/м,  переменных  ЭП.  В  этом  механизме  предполагается,  что  высота  барьера  W,  разделяющего  активное  и  неактивное  состояния  мембранного  белка-фермента  в  реакции  типа  Михаэлиса-Ментен,  см.  риc.  2,  меняется  согласованно  с  внешним  электрическим  полем.  Частотная  селективность  здесь  постулирована,  а  ее  природа  связывается  с  высоко  добротными  колебаниями  заряженной  группы  атомов  внутри  белка,  индуцированными  внешним  полем.  Эти  колебания  и  ведут  к  модуляции  высоты  барьера.  Очевидно,  здесь  игра  идет  не  на  изменении  вероятностей  состояний,  а  на  изменении  скоростей  перехода  между  этими  состояниями.  Согласно  теории  абсолютных  скоростей  реакций,  константу  скорости  прямой  и  обратной  реакции  можно  записать  следующим  образом: 

k_±1  =  k₀exp  −.  (15)

Вследствие  нелинейной  экспоненциальной  зависимости  констант  скоростей  переходов  от  высоты  барьера,  появляется  ненулевой,  в  среднем  по  времени,  вклад,  вызванный  внешним  переменным  ЭП.  Последнее  выражение  вполне  аналогично  (8),  откуда  заключаем,  что  относительное  изменение  скорости  реакции  того  же  порядка,  что  и  относительное  изменение  константы  равновесия,  то  есть  мало.  Этот  механизм  не  обладает  амплитудной  избирательностью.  К  тому  же,  количественные  оценки  были  основаны  на  ряде  модельных  предположений.  Главное  из  них  состояло  в  сомнительном  с  точки  зрения  физики  утверждении,  что  внешнее  ЭП  может  быть  усилено  плазматической  мембраной,  так  что  изменение  поля,  индуцированное  внутри  мембраны  приблизительно  в  R_cell/d_membr  раз  больше,  чем  исходное  внешнее  ЭП.  Утилизация  этого  механизма  в  процессах  биологической  рецепции  слабых  электрических  полей  остается  под  вопросом,  так  как  специальных  экспериментов  для  проверки  механизма  не  проводили.  Маркин,  Лиу  и  др.  [13]  предложили  модель  «электроконформационной  связи»,  которая  предсказывает  не  только  частотное,  но  и  амплитудное  окно.  Модель  основана  на  том,  что  как  состояние  иона  в  мембранном  белке-транспортере,  так  и  состояние  самого  транспортера  -  открыт  внутрь  или  наружу,  —  зависят  от  электрического  поля  и  являются  термически  активируемыми  процессами.  Взаимодействие  этих  процессов  ведет  к  возникновению  амплитудного  окна.  Частотное  окно  обусловлено  релаксационными  процессами,  как  и  в    [12].  Амплитудное  окно  определено  в  районе  2  кВ/м  для  (Na,  K)  ATФ-азы  эритроцитов  человека.  Это  слишком  много,  чтобы  пытаться  приспособить  модель  для  объяснения  частотно-  и  амплитудно-селективной  биорецепции  слабых  электрических  полей,  например,  полей,  индуцированных  в  биологической  ткани  низкочастотными  МП. 

Вивер  и  Астумиан  [11]  оценивают  предельную  чувствительность  клеточной  системы  к  электрическому  полю,  предполагая,  что  рецепция  ЭП  опосредована  каким-либо  процессом,  сходным  с  выше  разобранными  механизмами.  Такой  процесс  зависит  от  трансмембранной  разности  потенциалов.  Поэтому,  предельная  чувствительность  могла  бы  соответствовать,  по  предположению  авторов,  шумовым  флуктуациям  трансмембранной  разности  потенциалов.  Для  оценки  последних  использована  формула  Найквиста,  см.,  например  [14].  По  поводу  правомерности  использования  этой  формулы  необходимо  сделать  замечание.  Формула  следует  из  флуктуационно-диссипационной  теоремы  для  обобщенных  восприимчивостей  линейных  систем.  Такой  линейной  системой  в  частности  является  активное  электрическое  сопротивление.  Ток  в  цепи,  реакция  на  внешнее  электрическое  поле,  связан  с  напряженностью  поля  линейной  зависимостью.  Самое  главное  электрическое  свойство  плазматической  мембраны  состоит  в  ее  существенной  нелинейности.  Именно  это  свойство  обеспечивает  возникновение  трансмембранного  потенциала,  основы  для  процессов  нервной  возбудимости.  Приходится  признать,  что  в  данном  случае  общие  физические  закономерности  линейных  откликов  использованы  за  пределами  своей  применимости.  По  крайней  мере,  необходимо  обоснование  для  столь  сильной  идеализации.

Список  литературы:

1.Бинги  В.H.  О  модели:  ионный  канал-электрический  соленоид  //Биофизика.  —  1995.  —Т.  40,  —  №  3.  —С.  561—562.

2.Броун  Г.Р.,  Ильинский  О.  М.Физиология  электрорецепторов.  Л.:  Наука,  1984.

3.Лифшиц  Е.М.,  Питаевский  Л.  П.Статистическая  физика.  М.:  Hау-ка,  1978.  Т.  IX  из  Теоретическая  физика.  —  448  с.

4.Astumian  R.D.,  Weaver  J.C.,  Adair  R.K.Rectification  and  signal  averaging  of  weak  electric  fields  by  biological  cells  //P.  Natl.  Acad.  Sci.  USA.  —  1995.  —  Vol.  92.  —  Pp.  3740—3743.

5.Barnes  F.S.  A  model  for  detection  of  weak  ELF  electric  and  magnetic  fields  //Bioelectroch.  Bioener.  —  1998.  —  Vol.  47.  —  Pp.  207—212.

6.Binhi  V.N.,  Savin  A.V.  Molecular  gyroscopes  and  biological  effects  ofweak  extremely  low-frequency  magneticfields  //Phys.  Rev.  E.  —  2002.  —  Vol.  65,  —  №  051912.  —  Pp.  1—10.

7.Binhi  V.  N.  Interferenceof  ion  quantum  states  within  a  protein  explains  weak  magnetic  field’s  effect  on  biosystems  //Electro  Magnetobiol.  —  1997.  —  Vol.  16,  —  №  3.  —  Pp.  203—214.

8.Binhi  V.N.A  formula  for  frequency  and  amplitude  windows  of  some  EL  Fand  null  MF  bioeffects  follows  from  the  Schrodinger  equation  //  Electricity  and  Magnetism  in  Biology  and  Medicine  /  Ed.  by  F.  Bersani.  London:  Kluwer/Plenum,  1999.  —  Pp.  417—421.

9.Ion  channel  enzyme  in  an  oscillating  electric  field  /  V.S.  Markin,  D.  Liu,  J.  Gimsa  et  al.  //J.  Membr.  Biol.  —  1992.  —  Vol.  126.  —  Pp.  137—145.

10.Jungerman  R.L.,  Rosenblum  B.  Magnetic  induction  for  the  sensing  of  magnetic  fields  //J.  Theor.  Biol.  —  1980.  —  Vol.  87.  —  P.  25.

11.Kalmijn  A.  J.Electric  and  magnetic  field  detection  in  elasmobranch  fishes  //Science.  —  1982.  —  Vol.  218.  —  P.  916.

12.Pilla  A.A.,  Nasser  P.R.,  Kaufman  J.J.  Gap  junction  impedance,  tissue  di-electrics  and  thermal  noise  limits  for  electromagneticfield  bioeffects  //Bioelectroch.  Bioener.  —  1994.  —  Vol.  35.  —  Pp.  63—69.

13.Tsong  T.Y.  Molecular  recognition  and  processing  of  periodic  signals  in  cells:  study  of  activation  of  membrane  ATPase’s  by  alternating  electricfields  //Biochim.  Biophys.  Acta.  —  1992.  —  Vol.  1113.  —  Pp.  53—70.

14.Weaver  J.C.,  Astumian  R.D.  The  response  of  living  cells  to  very  weak  electric  fields:  The  thermal  noise  limit  //Science.  —  1990.  —  26  Jan.  —  Vol.  247.  —  Pp.  459—462.