СИНТЕЗ  ЗАКОНОВ  УПРАВЛЕНИЯ  ВЕРТОЛЕТОМ  АНСАТ  С  ПОМОЩЬЮ  ИНВЕРСНОЙ  МОДЕЛИ

Чекмарев  Сергей  Владимирович

студент  4  курса,  кафедра  АиУ  КНИТУ-КАИ,  РФ,  Республика  Татарстан,  г.  Казань

Е- mail: 

">slimercorp @gmail.com

Гаркушенко  Владимир  Иванович

научный  руководитель,  канд.  техн.  наук,  доцент  КНИТУ-КАИ,  РФ,  Республика  Татарстан,  г.  Казань

Введение

Из-за  свойственной  нестабильности  и  нелинейности  динамики  вертолета,  ее  изменяющихся  свойств  во  время  полета,  управление  полетом  вертолета  требует  специальных  стратегий.  Эти  стратегии  должны  справляться  с  нелинейностью  системы  и  гарантировать  устойчивость  в  присутствии  погрешностей  и  изменений  в  конфигурации.  В  данной  работе  на  примере  вертолета  Ансат  развивается  новый  подход  к  синтезу  управления  на  основе  инкрементной  нелинейной  динамической  инверсии  (ИНДИ)  [4,  c.  1065—1077].  Метод  основан  на  использовании  обратной  связи  по  ускорению,  что  позволяет  строить  законы  управления  при  минимальной  информации  о  модели  вертолета. 

В  качестве  объекта  управления  используется  математическая  модель  вертолета  Ансат  [1,  c.  18—21].

1.  Регулятор  угловых  скоростей

На  основе  ИНДИ  разработаем  регулятор  для  отслеживания  заданных  угловых  скоростей  вертолета  ,  искомое  управление  .

Используя  уравнение  динамики,  возьмем  производную  от    до  тех  пор,  пока  не  появится  прямая  зависимость  от  управления:

  ,

где:  J  —  тензор  инерции, 

M   —  вектор  моментов,  действующий  на  вертолет.  Поучив  прямую  зависимость  от  управления,  преобразуем  уравнение:

  ,

где 

,

.

Используем  виртуальное  управление    и  проведем  процедуру  разложения  в  ряд  Тейлора  последнего  уравнения:

.

Если  положить  ,  то  можно  записать

.

Отсюда  найдем

.

Для  реализации  полученного  закона  управления  должен  быть  известен  вектор  состояния  ,  управление    и  угловое  ускорение  .

Обозначим  Якобиан  и  рассмотрим  его  слагаемые. 

Первое  слагаемое  находится  из  уравнений  момента  вертолета: 

.

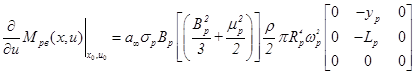Моментом  по  оси  Z  пренебрежем,  ввиду  его  малости.

Второе  слагаемое  вычисляется  аналогично:

  .

Общая  схема  регулятора  угловой  скорости  представлена  на  рис.  1.

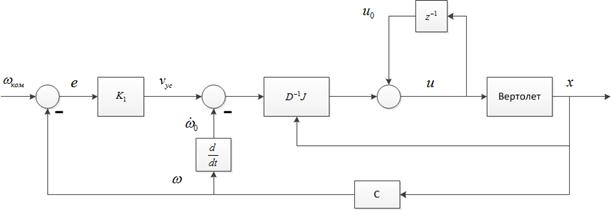
Рисунок  1.  Регулятор  угловых  скоростей  вертолета

2.  Регулятор  положения  вертолета

Регулятор  положения  вертолета  будет  отслеживать  заданные  углы  вертолета,  подавая  команды  желаемой  угловой  скорости  на  регулятор  угловой  скорости  вертолета.  Входной  вектор  регулятора  .

Дифференцируем  вектор    пока  зависимость  от  управления  не  появится:

.

Прямая  зависимость  от  управления  получена,  видим,  что  здесь  в  уравнении  нет  части,  которая  зависит  только  от  состояния  модели,  поэтому  применение  ИНДИ  не  даст  никаких  преимуществ,  воспользуемся  нелинейной  динамической  инверсией  (НДИ):

.

Отсюда  управление  выражается  как

.

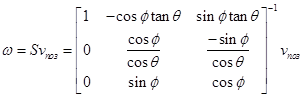Общая  схема  системы  вместе  с  регулятором  положения  представлена  на  рис.  2.

Рисунок  2.  Регулятор  углового  положения  вертолета

3.  Навигационный  регулятор

Для  управления  вертолетом  в  пространстве  добавим  к  разработанным  регуляторам  угловой  скорости  и  углового  положения  навигационный  регулятор,  который  на  основе  команд  по  линейным  скоростям,  связанные  с  землей,  будет  давать  команды  углам.

Входной  вектор  этого  регулятора:

  .

Используем  упрощенное  уравнение  кинематики  и  динамики:

,

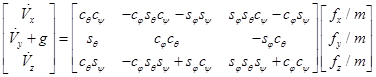где 

Можно  видеть,  что  это  уравнение  уже  содержит  первую  производную  от  выходного  вектора  и  зависимость  от  углов  уже  получена.

Виртуальное  управление  этого  регулятора  имеет  вид:

.

Чтобы  найти  нужные  углы  для  упрощенного  уравнения  кинематики  и  динамики  сделаем  некоторые  допущения:  угол    известен  заранее;  сила    на  порядок  больше  сил  ,  ,  поэтому  последними  можно  пренебречь. 

Тогда  можно  показать,  что  потребные  углы  тангажа  и  крена  определяются  по  формулам:

  ,

  .

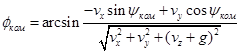В  случае,  когда  виртуальное  управление  равно  0,  например,  в  режиме  висения,  командные  углы  будут  также  равны  0,  следовательно,  нужно  к  найденным  значениям  углов  добавить  балансировочные  углы.

Такой  метод  управления  называется  аппроксимированная  динамическая  инверсия  (АДИ).

Для  разработки  закона  управления    используем  второе  уравнение  упрощенного  уравнения  кинематики  и  динамики.  Здесь  аналогично  предыдущему  находится  управление: 

,

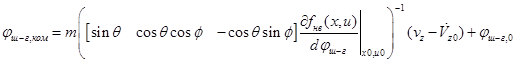где  .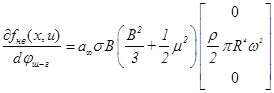

Общая  схема  регуляторов  на  основе  ИНДИ  представлена  на  рис.  3:

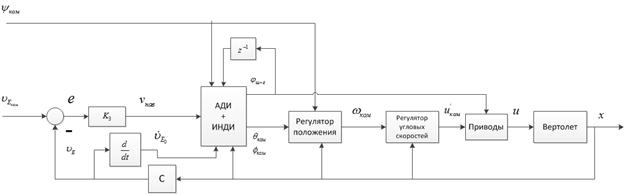
Рисунок  3.  Общая  схема  регуляторов  на  основе  ИНДИ

4.  Псевдо-хеджирование

Методика  псевдо-хеджирования  (ПХ)  служит  полезным  дополнением  к  регулятору  ИНДИ,  улучшая  его  работу.  Она  выполняет  несколько  функций:

a.   устанавливает  ограничение  командным  сигналам  до  безопасного  уровня;

b.  помогает  предотвратить  насыщение  приводов;

c.   вычисляет  производную  от  командного  сигнала  для  использования  регулятором  его  как  опережающей  связи;

d.  играет  роль  фильтра,  сглаживая  процессы.

ПХ  состоит  из  двух  блоков:  эталонной  модели  (рис.  4)  и  самого  блока  ПХ.

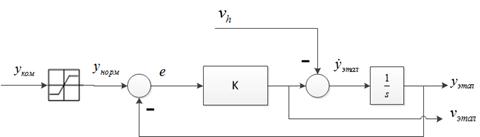
Рисунок  4.  Схема  эталонной  модели

Эталонная  модель  имеет  вид  фильтра  низкой  частоты  с  частотой  среза  равной  K  (функция  d).  Командный  сигнал  проходит  через  блок  насыщения  (функция  a),  и  далее  вычисляется  его  производная,  из  которой  вычитается  сигнал  от  PCH  (функция  b),  с  этого  момента  берется  опережающий  сигнал  (функция  c). 

Сам  блок  ПХ  вычисляет  переменную    для  эталонной  модели.  Смысл  заключается  в  том,  что  если  достигается  насыщение  привода,  то  блок  ПХ  вычисляет  превышение  виртуального  управления  и  посылает  команду  эталонной  модели  вычесть  превышенное  виртуальное  управление  из  эталонной  команды,  чтобы  избежать  насыщения  и  сохранить  устойчивость.

Пример  общей  схемы  управления  на  основе  НДИ  с  ПХ  представлен  на  рис.  5.

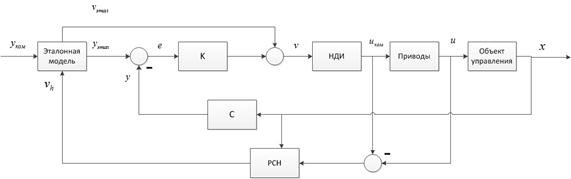
Рисунок  5.  Схема  закона  управления  вместе  с  ПХ

5.  Синтез  коррекции

В  методе  ИНДИ  не  учитывается  динамика  датчиков  и  исполнительных  устройств,  которая  приводит  к  ухудшению  качества  процессов  управления.  В  связи  с  этим  в  данной  работе  предлагается  использовать  корректирующие  устройства  для  компенсации  неучтенной  динамики  датчиков  и  приводов.

Для  вертолета  Ансат  приняты  инерционности  исполнительных  устройств  и  датчиков  в  виде  апериодических  звеньев:  для  циклического  шага  с  постоянной  времени  0.05  c;  для  общего  шага  НВ  и  РВ  с  постоянной  времени  0.03  c;  динамика  датчиков  вместе  с  фильтрацией  с  постоянной  времени  0.07  с.

При  учете  динамики  приводов  и  датчиков  в  математической  модели  вертолета  качество  процессов  управления  ухудшилась  по  сравнению  с  процессами,  полученными  при  синтезе  управления  без  учета  указанной  инерционности  по  методике  [1,  c.  18—21].  Поэтому  введем  дискретное  корректирующее  устройство  с  периодом  дискретности  0.01  с.  для  каждого  канала  управления.  Синтез  последовательного  корректирующего  устройства  проводится  методом  ЛАХ  по  разомкнутой  передаточной  функции  канала  с  целью  задания  желаемых  запасов  по  фазе  и  амплитуде  [2,  с.  168].

На  рис.  6  отображены  частотные  характеристики  этого  канала  до  (зеленая  линия)  и  после  (синяя  линия)  введения  динамики  приводов  и  датчиков.  Из  графика  можно  увидеть,  что  до  введения  инерционности  частота  среза  равнялась  56  рад/с.

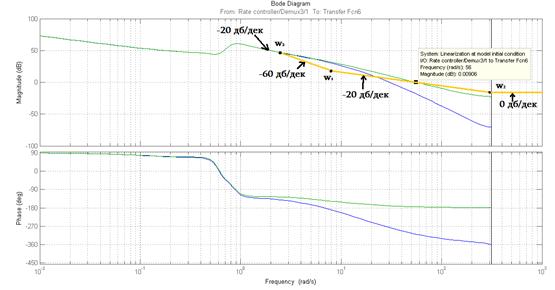
Рис унок  6.  Частотные  характеристики  канала  до  и  после  введения  запаздывания,  а  также  построение  ЛАХ  желаемой  системы

Также  на  этом  рисунке  изображена  построенная  ЛАХ  желаемой  системы  (оранжевая  линия),  с  помощью  которой  была  получена  передаточная  функция  коррекции:

.

Реакция  скорректированной  системы  на  скачок  представлена  на  рис.  7—10,  где  пунктирной  линией  отмечены  процессы  до  введения  инерционности  приводов  и  датчиков.

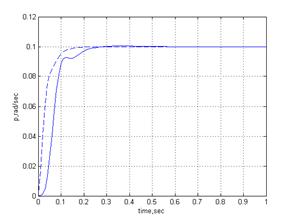
Рисунок  7.  Реакция  угл.  скорости  крена  на  скачок  0.1  рад/сек.

Рисунок  8.  Реакция  угл.  скорости  тангажа  на  скачок  0.1  рад/сек.

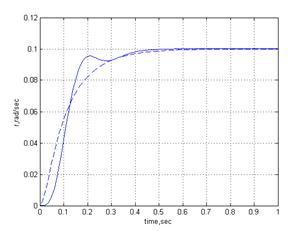
Рисунок  9.  Реакция  угл.  скорости  курса  на  скачок  0.1  рад/сек.

Рисунок  10.  Реакция  верт.  C корости  на  скачок  1  м/c.

Работоспособность  синтезированной  системы  управления  также  подтверждена  моделированием  режимов  полета  вертолета  пируэт,  разгон-торможение  по  спецификации  ADS-33  [3],  а  также  при  исследовании  законов  управления  на  лабораторном  вертолетном  стенде.

Выводы

С  помощью  предлагаемого  подхода  разработаны  3  регулятора  с  разделением  быстрой  и  медленной  динамики  вертолета  Ансат:  регулятор  угловых  скоростей,  регулятор  углового  положения  и  навигационный  регулятор.  При  разработке  закона  управления  использовалась  модель  управляющих  моментов  вертолета.  Во  внешнем  контуре  навигационного  управления  была  применена  методика  ИНДИ  только  для  управления  вертикальной  скоростью,  а  для  продольной  и  поперечной  скорости  использовалась  методика  АДИ.

Результаты  моделирования  с  найденными  законами  управления  показали  высокую  производительность  внутреннего  контура  и  управления  вертикальной  скоростью,  а  также  хорошее  качество  процессов  управления  при  наличии  возмущений  и  неопределенностей. 

Достоинством  разработанного  регулятора  является  высокая  производительность  и  хорошая  робастность  к  возмущениям  и  неопределенностям.  Для  синтеза  управления  не  требуется  полной  информации  о  модели  вертолета,  что  позволяет  существенно  сократить  время  для  настройки  алгоритмов  управления. 

Работа  поддержана  грантом  Правительства  РФ  для  государственной  поддержки  научных  исследований  по  постановлению  Правительства  220  по  договору  от  30  декабря  2010  г.  №  11.G34.31.0038.

Список  литературы :

1.Гаркушенко  В.И.,  Безбрязов  М.В.,  Баракос  Д.  Синтез  корректирующего  закона  управления  для  повышения  качества  стабилизации  вертолета  //  Изв.  вузов.  Авиационная  техника.  2012.  №  3.

2.Гаркушенко  В.И.,  Дегтярев  Г.Л.  Теория  автоматического  управления,  учебное  пособие.  Казань,  2010.

3.Aeronautical  design  standard  performance  specification:  handling  qualities  requirements  for  military  rotorcraft  —  2000  —  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.everyspec.com/ARMY/ADS-Aero-Design-Std/ADS-33E-PRF_3614/  (дата  обращения  27.10.2013).

4. Simplicio  P.,  Pavel  M.D.,  Kampen  E.,  Chu  Q.P.  An  acceleration  measurements-based  approach  for  helicopter  nonlinear  flight  control  using  Incremental  Nonlinear  Dynamic  Inversion  //  Control  Engineering  Practice,  №  21,  2013.