Статья опубликована в рамках: XIX Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 15 апреля 2014 г.)
Наука: Технические науки
Секция: Энергетика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОЦЕНКА ВЛИЯНИЯ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ ТОКОВЕДУЩИХ ЧАСТЕЙ НА РАСЧЕТ НЕСИНУСОИДАЛЬНЫХ РЕЖИМОВ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ
Сатпаев Дмитрий Сергеевич
студент 4 курса, кафедра Электроснабжение промышленных предприятий ОмГТУ, РФ, г. Омск
E -mail: satpaevdmitriy.kz@yandex.ru
Логунова Яна Юрьевна
студент 4 курса, кафедра Электроснабжение промышленных предприятий ОмГТУ, РФ, г. Омск
E -mail: jana_logunova@mail.ru
Розинкин Данил Анатольевич
студент 4 курса, кафедра Электроснабжение промышленных предприятий ОмГТУ, РФ, г. Омск
E -mail: danil_2@mail.ru
Мохова Дарья Владимировна
магистрант 1 курса, кафедра Электроснабжение промышленных предприятий ОмГТУ, РФ, г. Омск
E -mail: gvadamichdi2009@yandex.ru
Осипов Дмитрий Сергеевич
научный руководитель, канд. техн. наук, доцент ОмГТУ, РФ, г. Омск
E -mail: ossipovdmitriy@list.ru
Проблема обеспечения качества электроэнергии (КЭ) является одной из важнейших, определяющих надежность и эффективность электроснабжения потребителей. Отрицательное действие некачественной электроэнергии для энергосистем имеет следующие отрицательные последствия [2]:
1. Возникают дополнительные потери мощности и энергии;
2. Повышается температура проводов линий электропередачи, а также обмоток трансформаторов и вращающихся электрических машин, которая может превысить допустимый уровень;
3. Ускоряется процесс старения изоляции;
4. Ухудшается работа потребителей электроэнергии, вследствие чего могут возникать сбои технологических процессов;
5. Могут возникать нарушения работы устройств релейной защиты, автоматики и телемеханики;
6. Увеличивается погрешность электроизмерительных приборов;
7. Сокращается срок службы конденсаторных установок из-за их перегрузки токами высших гармоник.
Ущерб в целом по Российской Федерации от некачественной электроэнергии по таким её свойствам, как отклонение и несинусоидальность напряжения, а также несимметрия трехфазной системы напряжения, составил, по экспертным оценкам, примерно 20 млрд. руб. в год. Попытки практической реализации требований в АО Энерго выявили целый ряд нерешенных вопросов по научному, организационно-методическому, нормативно-правовому и приборному обеспечению этих мероприятий. Поэтому в данной работе сделана попытка рассмотрения возможных подходов к решению вопросов, связанных с обеспечением качества электроэнергии и ее сертификацией. На практике возникают задачи оценки экономичности и допустимости несинусоидальных режимов, а также выбора мероприятий по снижению уровня несинусоидальности.
Несинусоидальные режимы являются в большинстве случаев неэкономичными и могут быть технически недопустимыми. Для решения задач оценки экономичности и допустимости этих режимов, а также для выбора мероприятий по снижению уровня несинусоидальности необходимо более точное моделирование элементов сети, нагрузок и источников питания.
Элементы сети при расчете несинусоидальных режимов обычно представляются в виде схем замещения с линейными сопротивлениями и проводимостями [2]. Однако в действительности часть этих сопротивлений и проводимостей являются нелинейными. Одним из видов этой нелинейности является нелинейность активных сопротивлений проводников вследствие температурной зависимости, которая выражается формулой
![]() , (1)
, (1)
где: R0 — активное сопротивление при нуле градусов Цельсия;
α — температурный коэффициент сопротивления;
Θп – температура проводника;
R – активное сопротивление при температуре Θп.
Сопротивление элементов сети может за счет изменений температуры изменяться примерно на 40% и, настолько же могут измениться и потери мощности. Следовательно, в расчетах необходимо учитывать температуру.
Для того чтобы рассчитать несинусоидальный режим с учетом температуры, необходимо в той или иной форме задать функциональную зависимость температуры проводников от параметров режима электрической сети. Эта зависимость для разных элементов сети имеет разный вид, который определяется уравнениями теплового баланса. В простейшем случае при симметричной токовой нагрузке в стационарном тепловом режиме уравнение теплового баланса имеет следующий вид:
![]() , (2)
, (2)
где: Iν — действующее значение тока ν-й гармоники;
Rν ,0 — активное сопротивление току ν-й гармоники при нуле градусов Цельсия;
A — коэффициент теплоотдачи;
Θокр — температура окружающей среды.
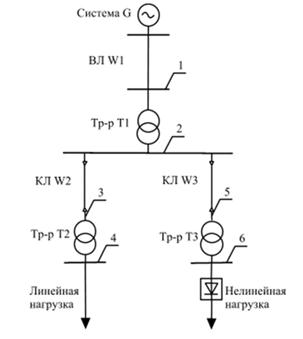
Рисунок 1. Исследуемая схема СЭС
В ходе проводимых исследований автором ставилась задача оценить степень влияния учета высших гармоник на потери активной мощности.
Так, для схемы, представленной на рисунке 1 проводился ряд вычислительных экспериментов.
Так как температура проводника определяется всем спектром гармоник тока, то для расчета несинусоидальных режимов с учетом температуры метод наложения в чистом виде неприменим. Поэтому в разработанной методике предлагается использование итерационного подхода. Последовательность расчета в стационарном тепловом режиме представляет собой следующее:
1. Задаются начальные приближения температур проводников;
2. Производится расчет несинусоидального режима по методу наложения при принятых температурах;
3. Из уравнений теплового баланса определяются следующие приближения температур и сравниваются с предыдущими. Если все расхождения (невязки) находятся в пределах заданной точности, то расчет заканчивается. В противном случае осуществляется возврат к пункту 2.
Если тепловой режим нестационарен, то уравнения теплового баланса являются дифференциальными. В этом случае режим сети изменяется во времени и может быть рассчитан путем численного решения уравнений нагрева совместно с электрическими уравнениями например, с уравнениями узловых потенциалов. Уравнения теплового баланса элементов сети приведены в таблице 1.
Таблица 1.
Уравнения теплового баланса элементов сети
|
Тип элемента |
Уравнения |
Пояснения |
|
Кабель 6—10 кВ, проложенный в воздухе |
|
DP — потери активной мощности в ЛЭП; Θж — превышение температуры жилы кабеля над температурой окружающей среды; Θп — превышение температуры поверхности кабеля над температурой окружающей среды; Sк — тепловое сопротивление кабеля; Aк — постоянный коэффициент, характеризующий интенсивность теплоотдачи от кабеля в воздух; Sз — тепловое сопротивление грунта; F — площадь поверхности провода; Θпр — температура провода; Θокр — температура окружающей среды; |
|
Кабель 6—10 кВ, проложенный в земле |
|
|
|
Воздушная линия с неизолированными проводами |
|
|
|
Сухой трансформатор |
|
|
|
Масляный трансформатор с естественной циркуляцией масла |
|
|
|
Масляный трансформатор с принудительной циркуляцией масла |
|
Параметры расчетной схемы электроснабжения (рис. 1) приведены в табл. 2 и 3.
Таблица 2.
Параметры линий
|
Тип и номинальное напряжение |
№ линии |
марка |
Сечение F , мм2 |
Допус тимый ток I доп, А |
Допустимая температура t доп , °С |
Длина L , км |
Окружа ющая среда |
|
ВЛЭП 110 кВ |
W1 |
АС |
120 |
390 |
+70 |
10 |
Воздух |
|
КЛЭП 10 кВ |
W2, W3 |
АПсшБбШв |
35 |
136 |
+90 |
5 |
Воздух |
Таблица 3.
Параметры трансформаторов
|
№ трансформатора |
Номинальная мощность S ном, кВּА |
Номинальное напряжение U вн/ Uнн, кВ |
Допустимая температура t доп ,°С |
Тип |
|
Т1 |
6300 |
115/11 |
+85 |
Масляный |
|
Т2,Т3 |
2500 |
11/0,69 |
+85 |
Масляный |
Следует отметить, что неучет нагрева токоведущих частей может приводить к значительным погрешностям при расчете потерь мощности и энергии [3]. Так для трансформатора Т3 был проведен вычислительный эксперимент по определению погрешности расчета потерь мощности при учете и неучете температуры (рис. 2, табл. 4.):

Рисунок 2. Расчет потерь мощности в трансформаторе с учетом и без учета температуры
На основании приведенных данных можно заключить, что при загрузке более некоторого значения погрешность начинает превышать допустимый предел точности 5 %. А для данного случая, при коэффициенте загрузки трансформатора 0,8 погрешность достигает 21,6 %, что довольно значительно.
Таблица 4.
Расчет погрешности определения потерь мощности в трансформаторе
|
Коэффициент Загрузки , о.е. |
Потери мощности при учете температуры, ∆Pt , Вт |
Потери мощности без учета температуры, ∆P , Вт |
Погрешность определения потерь мощности, ∆P , % |
|
0,1 |
250,5 |
240,1 |
4,2 |
|
0,2 |
1031,3 |
978,97 |
5,1 |
|
0,3 |
2405,1 |
2249,4 |
6,5 |
|
0,4 |
4465,9 |
4092,1 |
8,4 |
|
0,5 |
7347,8 |
6556,1 |
10,8 |
|
0,6 |
11246,4 |
9702,9 |
13,7 |
|
0,7 |
16447,3 |
13605,1 |
17,3 |
|
0,8 |
23407,3 |
18360 |
21,6 |
Неучет температуры окружающей среды может также внести определенного рода погрешность в расчет сопротивления. Для оценки этой погрешности был произведен вычислительный эксперимент [1] при базисных условиях, представленных в таблице 2,3 при изменении температуры окружающей среды от –30 до +20ºС. Были получены следующие (таблица 5, рисунок 3) результаты для элементов W3 и Т3.
Таблица 5.
Расчет потерь при различных температурах окружающей среды
|
Температура окружающей среды t, ºС |
Потери активной мощности в трансформаторе T3, Вт |
Потери активной мощности в линии W3, Вт |
|
-30 |
19 160 |
33 559 |
|
-25 |
19 607 |
34 388 |
|
-15 |
20 054 |
35 218 |
|
-10 |
20 503 |
36 050 |
|
-5 |
20 952 |
36 883 |
|
0 |
21 402 |
37 718 |
|
5 |
21 853 |
38 555 |
|
10 |
22 304 |
39 393 |
|
15 |
22 756 |
40 233 |
|
20 |
23 209 |
41 075 |
Следует отметить, что при указанных базисных условиях диапазон изменения расчета потерь мощности составляет 20—25 % для кабельной линии и трансформатора.
На основании вышеизложенного можно сделать вывод, что учет окружающей температуры, для кабельных линий, проложенных в воздухе и в случае значительных перепадов между зимними и летними температурами обязателен.

Рисунок 3. Расчет потерь мощности при различных температурах окружающей среды
Полученная погрешность достаточно велика, чтобы считать обоснованным учет нагрева токоведущих частей при выборе мероприятия по снижению потерь. Уточнение расчета потерь позволит инженерным службам предприятий более точно рассчитывать балансы потребления электроэнергии при проведении энергетических обследований. Как правило, вследствие неточности расчета потерь существует практика относить невязку баланса к коммерческим потерям, что в конечном итоге пагубно отражается на потребителе энергоресурсов. Полученные в работе результаты могут быть полезны также на стадии проектирования, поскольку уточнение расчета потерь позволит в значительной степени уточнить технико-экономические расчеты.
Список литературы:
1.Горюнов В.Н. Расчет потерь мощности от влияния высших гармоник /Горюнов В.Н., Осипов Д.С., Лютаревич А.Г. [текст] // Научные проблемы транспорта Сибири и Дальнего Востока. — 2009. — № 2. — С. 268—273.
2.Осипов Д.С. Учет нагрева токоведущих частей в расчетах потерь мощности и электроэнергии при несинусоидальных режимах систем электроснабжения: Дис. на соиск. уч. степ. канд. техн. наук [текст] / Д.С. Осипов – Омский государственный технический университет. Омск, 2005. — 152 с.
3.Шидловский А.К. Высшие гармоники в низковольтных электрических сетях / Шидловский А.К., А.Ф. Жаркин [монография] //Киев. Наукова думка. 2005. — 210 с.
дипломов


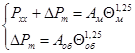

Оставить комментарий