"За статью проголосовало 1520 человек"

СВОЙСТВА  ГЕОМЕТРИЧЕСКОГО  МЕСТА  ЦЕНТРОВ  ЗАМКНУТОЙ  СИСТЕМЫ  ТЕЛ  КАЧЕНИЯ  С  ДИАМЕТРАМИ  РАЗНОЙ  ВЕЛИЧИНЫ

Кутина  Алина  Андреевна

студент  4  курса,  кафедра  «Стандартизация,  метрология  и  управление  качеством»,  Политехнический  институт  ФГАОУ  ВПО  «Сибирский  федеральный  университет»,  РФ,  г.  Красноярск

E-mail:  Kutina_alina@mail.ru

Мерко  Алексей  Михайлович

студент  1  курса,  кафедра  «Вычислительная  техника»,  Институт  космических  и  информационных  технологий  ФГАОУ  ВПО  «Сибирский  федеральный  университет»,  РФ,  г.  Красноярск

E-mail:  mimaa2008@rambler.ru

Мерко  Михаил  Алексеевич

научный  руководитель,  канд.  тех.  наук,  доцент,  доцент  кафедры  «Прикладная  механика»  Политехнического  института  ФГАОУ  ВПО  «Сибирский  федеральный  университет»,  РФ,  г.  Красноярск

Меснянкин  Марк  Вадимович

научный  руководитель,  старший  преподаватель  кафедры  «Прикладная  механика»  Политехнического  института  ФГАОУ  ВПО  «Сибирский  федеральный  университет»,  РФ,  г.  Красноярск

К  группе  основных  характеристик  преобразующих  механизмов  любого  вида  относятся  геометрические  параметры,  взаимодействие  которых  обеспечивает  требуемые  величины  показателей  качества,  как  самого  механизма,  так  и  привода  технологического  оборудования  в  целом.  Правильное  решение  задачи  по  определению  величин  геометрических  параметров  возможно  только  при  учете  всех  особенностей  геометрии  и  структуры  преобразующего  механизма  конкретного  вида  используемого  при  формировании  привода  технологического  оборудования.  Поиск  рациональной  структуры  при  минимально  возможном  числе  подвижных  звеньев  и  соединений  позволяет  исключить  или  существенно  сократить  количество  особенностей  геометрии,  а  также  обеспечить  реализацию  законов  движения  любой  сложности  и  получить  требуемые  величины  показателей  качества,  как  преобразующего  механизма,  так  и  всего  привода  технологического  оборудования.  Разработка  и  последующие  исследования  механизмов  с  подобными  свойствами  является  весьма  актуальной  задачей  на  данном  этапе  развития  экономики  России,  требующей  модернизации  промышленности  при  использовании  механизмов  обеспечивающих  рациональное  сочетание  показателей  качества  приводов  технологического  оборудования.

К  механизмам  соответствующим  описанным  условиям  относятся  и  механизмы  с  замкнутой  системой  тел  качения  (ЗСТК).  Механизмы  данного  вида  обладают  структурой  содержащей  два  кольца  с  дорожками  качения,  сепаратор  (водило)  и  замкнутую  систему  тел  качения  с  диаметрами  как  разной  (эксцентриковые),  так  и  равной  величины  (соосные).  Тела  качения  могут  обладать  рабочими  поверхностями  с  выступами  (зубчатые)  [1—4]  или  гладкими  поверхностями  (фрикционные)  [5—21].

Механизм  с  ЗСТК  с  диаметрами  равной  величины  является  механизмом-прототипом  механизмов  с  ЗСТК  с  диаметрами  разной  величины,  для  которых  характерно  смещение  центров  дорожек  качения  наружного  и  внутреннего  колец  содержащихся  в  структуре  на  величину  эксцентриситета.  Следовательно,  механизмы  рассматриваемого  вида  можно  отнести  к  разновидностям  эксцентриковых  механизмов  качения  (ЭМК).  Для  ЭМК  характерно  отсутствие  вертикальной  и  наличие  горизонтальной  оси  симметрии,  что  обеспечивает  существование  нескольких  видов  симметричных  структурных  схем  как  при  наличии,  так  и  при  отсутствии  зазора  между  телами  качения  (рис.  1).

Если  центра  тел  качения  механизмов  с  замкнутой  системой  тел  качения  принять  за  геометрическое  место  точек,  то  соединив  их,  получим  кривую  второго  порядка  не  зависимо  от  вида  симметричной  структурной  схемы  (рис.  1).  При  наличии  в  структуре  замкнутой  системы  тел  качения  с  диаметрами  равной  величины  данная  кривая  является  частным  случаем  кривой  второго  порядка,  т.  е.  окружностью.  В  случае  замкнутой  системы  тел  качения  с  диаметрами  разной  величины  обеспечивается  существование  эксцентриситета  посредствам  смещения  центров  дорожек  качения  наружного  и  внутреннего  колец.  В  этом  случае  возникает  потребность  уточнения  вида  кривой,  соединяющей  центра  тел  качения.  С  целью  установления  вида  данной  кривой  получим  ее  уравнение.

Рисунок  1.  Виды  симметричных  структурных  схем  механизмов  с  ЗСТК  с  диаметрами  разной  величины  (ЭМК):  а  —  при  наличии  зазора  между  телами  качения;  б  —  при  отсутствии  зазора  между  телами  качения

Составим  расчетную  модель  для  механизма  с  ЗСТК  с  диаметрами  разной  величины  (рис.  2),  а  также  примем  следующие  исходные  условия  и  обозначения:  ,    —  дорожки  качения  внутреннего  и  наружного  колец;  R_В,  R_Н,  О_В  и  O_Н  —  радиусы  и  геометрические  центры  дорожек  качения  концентрически  расположенных  внутреннего  и  наружного  колец;    —  левая  система  координат  с  центром  в  точке  O_Н;  e  —  эксцентриситет;  С  —  сепаратор  (водило);  c  —  зазор  между  телами  качения;  r₀,  r₁,  r_i  и  x₀,  x₁,  y₁  —  радиусы  и  координаты  максимального,  первого  и  i-го  тел  качения.

Рисунок  2.  Расчетная  модель  механизма  с  ЗСТК

Из  анализа  прямоугольных  треугольников    и  ,  содержащихся  на  расчетной  модели  механизмов  с  замкнутой  системой  тел  качения  с  диаметрами  разной  величины  (рис.  2),  будем  иметь

  (1)

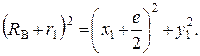  (2)

Проведя  преобразования  (1)  и  (2)  приведем  к  виду

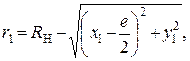  (3)

  (4)

Приравняем  (3)  и  (4)

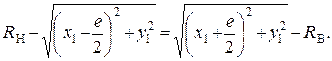  (5)

Проведя  соответствующие  преобразования,  приведем  уравнение  (5)  к  каноническому  виду

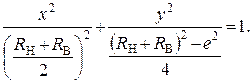  (6)

Выражение  (6)  является  уравнением  частного  случая  кривой  второго  порядка  являющейся  эллипсом,  соединяющим  центра  тел  качения  механизмов  с  ЗСТК  с  диаметрами  разной  величины  (ЭМК)  для  любого  вида  структурной  схемы  как  с  зазором  (рис.  1,  а),  так  и  при  отсутствии  в  структуре  данного  параметра  (рис.  1,  б).

Модули  полуосей  эллипса  получим  из  анализа  равенства  (6)

большая  полуось    (7)

малая  полуось 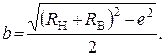   (8)

Из  свойств  эллипса  следует,  данный  вид  кривой  второго  порядка  является  частным  случаем  другого  вида  кривой  второго  порядка  называемой  окружностью  обладающей  геометрической  характеристикой  не  равной  единице.  Под  геометрической  характеристикой  подразумевается  степень  сжатия  рассматриваемой  кривой.  Значение  геометрической  характеристики  эллипса  определяется  отношением  полуосей  или  по  выражению

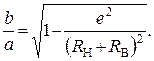  (9)

Анализ  равенства  (9)  показывает:  геометрическая  характеристика  эллипса  (отношение  полуосей)  лежит  в  пределах  от  0,94  до  0,98.

Из  свойств  эллипса  известно,  что  его  фокусы  лежат  на  большей  полуоси  расположенной  на  оси  X_H  (рис.  2).  Следовательно,  координаты  фокусов  эллипса    равны  нулю,  а  координаты    определим  по  выражению

  (10)

C  учетом  (7)  и  (8)  равенство  (10)  примет  вид

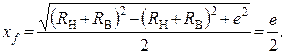  (11)

Анализ  расчетной  модели  (рис.  2)  и  равенства  (11)  показывает:  фокусы  эллипса,  являющегося  кривой  соединяющей  центра  тел  качения  механизмов  с  ЗСТК  с  диаметрами  разной  величины  (ЭМК),  имеют  координаты  (-0,5e;  0)  и  (0,5e;  0).  Это  означает,  что  фокусы  эллипса  совпадают  с  центрами  дорожек  качения  наружного  и  внутреннего  колец,  а  центр  эллипса  совпадает  с  точкой  О_С,  расположенной  по  центру  эксцентриситета  (рис.  2).

В  результате  выполненных  действий  установлены  свойства  геометрического  места  центров  замкнутой  системы  тел  качения  с  диаметрами  разной  величины  для  любого  вида  структурной  схемы  механизма  (рис.  1).  Установлено,  фокусы  данной  кривой  совпадают  с  центрами  дорожек  качения  наружного  и  внутреннего  колец,  а  её  центр  совпадает  с  точкой  О_С,  лежащей  по  центру  эксцентриситета  (рис.  2).  Выявленные  особенности  геометрии  необходимо  учитывать  при  решении  задачи  по  определению  номинальных  величин  геометрических  параметров  механизмов  с  ЗСТК.

Список  литературы:

1.Беляков  Е.В.,  Колотов  А.В.,  Мерко  М.А.,  Меснянкин  М.В.  Применение  САПР  при  исследовании  эксцентрикового  планетарного  механизма  //  Современные  технологии.  Системный  анализ.  Моделирование.  —  2012.  —  №  3.  —  С.  109—112.

2.Беляков  Е.В.,  Мерко  М.А.,  Колотов  А.В.,  Меснянкин  М.В.,  Митяев  А.Е.  Обеспечение  требуемого  движения  выходного  звена  эксцентрикового  эпициклического  механизма  //  Сборник  научных  трудов  Sworld  по  материалам  международной  научно-практической  конференции.  —  2012.  —  Т.  5.  —  №  4.  —  С.  47—51.

3.Белякова  С.А.,  Груздев  Д.Е.,  Беляков  А.Н.,  Мерко  М.А.,  Меснянкин  М.В.,  Колотов  А.В.  Применение  дифференциального  механизма  для  шлифования  плоских  поверхностей  //  Сборник  научных  трудов  Sworld  по  материалам  международной  научно-практической  конференции.  —  2012.  —  Т.  5.  —  №  4.  —  С.  51—56.

4. Колотов  А.В.,  Мерко  М.А.,  Меснянкин  М.В,  Беляков  Е.В.  Автоматизированное  проектирование  зубчатых  механизмов  приводов  технологического  оборудования  со  связанными  цилиндрическими  колесами  //  Современные  технологии.  Системный  анализ.  Моделирование.  —  2012.  —  №  4.  —  С.  51—57.

5.Мерко  М.А.  Кинематические  и  геометрические  характеристики  эксцентрикового  механизма  качения:  автореф.  дис.  канд.  техн.  наук:  05.02.02.  Красноярск,  2002.  —  26  с.

6.Мерко  М.А.,  Меснянкин  М.В.,  Митяев  А.Е.,  Колотов  А.В.  Анализ  взаимозависимостей  геометрических  параметров  эксцентрикового  механизма  качения  //  Вестник  Красноярского  государственного  аграрного  университета.  —  2012.  —  №  11.  —  С.  180—184.

7.Мерко  М.  А.,  Меснянкин  М.  В.,  Митяев  А.  Е.  Описание  математической  модели  механизма-прототипа  ЭМК  с  сепаратором  (водило)  при  ведущем  внутреннем  кольце  //  Молодой  ученый.  —  2013.  —  №  3.  —  С.  71—75.

8.Мерко  М.А.,  Меснянкин  М.В.,  Колотов  А.В.  Определение  координат  звеньев  механизма  с  замкнутой  системой  тел  качания  с  диаметрами  равной  величины  //  Актуальные  проблемы  гуманитарных  и  естественных  наук.  —  2013.  —  №  3.  —  С.  68—73.

9.Мерко  М.А.,  Меснянкин  М.В.,  Колотов  А.В.  Формирование  областей  существования  механизма  с  ЗСТК  с  диаметрами  равной  величины  с  сепаратором  (водило)  при  вводе  поправки  по  дорожке  качения  наружного  кольца  //  Молодой  ученый.  —  2013.  —  №  4.  —  С.  76—80.

10.Мерко  М.А.,  Меснянкин  М.В.,  Колотов  А.В.  Формирование  областей  существования  механизма  с  ЗСТК  с  диаметрами  равной  величины  с  сепаратором  (водило)  при  вводе  поправки  по  дорожке  качения  внутреннего  кольца  //  Актуальные  проблемы  гуманитарных  и  естественных  наук.  —  2013.  —  №  4.  —  С.  54—58.

11. Мерко  М.А.,  Меснянкин  М.В.,  Митяев  А.Е.  Зависимость  областей  существования  механизмов  с  ЗСТК  с  диаметрами  равной  величины  и  зазора  между  телами  качения  при  вводе  поправкой  по  дорожке  качения  внутреннего  кольца  //  Молодой  ученый.  —  2013.  —  №  5.  —  С.  79—83.

12.Мерко  М.А.,  Меснянкин  М.В.,  Колотов  А.В.  Передаточные  отношения  механизмов  с  ЗСТК  с  диаметрами  равной  величины  и  зазором  при  ведущем  внутреннем  кольце  и  вводе  поправки  по  дорожке  качения  наружного  кольца  //  Молодой  ученый.  —  2013.  —  №  6.  —  С.  71—75.

13.Мерко  М.А.,  Меснянкин  М.В.,  Митяев  А.Е.  Передаточные  отношения  механизмов  с  ЗСТК  с  диаметрами  равной  величины  и  зазором  при  ведущем  наружном  кольце  и  вводе  поправки  по  дорожке  качения  внутреннего  кольца  //  Актуальные  проблемы  гуманитарных  и  естественных  наук.  —  2013.  —  №  6.  —  С.  63—68.

14.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.,  Митяев  А.Е.  Определение  границ  областей  существования  механизмов-прототипов  эксцентрикового  механизма  качения  при  вводе  поправки  в  расчет  по  дорожке  качения  внутреннего  кольца  //  Вестник  Красноярского  государственного  аграрного  университета.  —  2012.  —  №  12.  —  С.  138—142.

15.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.,  Митяев  А.Е.,  Белякова  С.А.  Определение  границ  областей  существования  механизма-прототипа  ЭМК  без  сепаратора  при  вводе  поправки  по  дорожке  качения  наружного  кольца  //  Сборник  научных  трудов  Sworld  по  материалам  международной  научно-практической  конференции.  —  2013.  —  Т.  3.  —  №  1.  —  С.  33—38.

16.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.,  Беляков  Е.В.,  Белякова  С.А.  Математическая  модель  ЭМК  с  сепаратором  при  ведущем  внутреннем  кольце  //  Сборник  научных  трудов  Sworld  по  материалам  международной  научно-практической  конференции.  —  2012.  —  Т.  5.  —  №  4.  —  С.  62—67.

17.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.,  Митяев  А.Е.  Результаты  решения  задачи  о  положениях  звеньев  ЭМК  при  ведущем  внутреннем  кольце  //Вестник  Таджикского  технического  университета.  —  2013.  —  №  1.  —  С.  35—41.

18.Меснянкин  М.В.,  Мерко  М.А.,  Митяев  А.Е.,  Колотов  А.В.,  Груздев  Д.  Е.  Особенности  геометрии  симметричных  структурных  схем  механизмов  с  ЗСТК  с  диаметрами  разной  величины  //  Сборник  научных  трудов  Sworld  по  материалам  международной  научно-практической  конференции.  —  2013.  —  Т.  4.  —  №  2.  —  С.  55—61.

19.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.  Зависимость  областей  существования  механизмов  с  ЗСТК  с  диаметрами  равной  величины  и  зазора  между  телами  качения  при  вводе  поправки  по  дорожке  качения  наружного  кольца  //  Актуальные  проблемы  гуманитарных  и  естественных  наук.  —  2013.  —  №  5.  —  С.  85—89.

20.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.,  Митяев  А.Е.  Моделирование  результатов  решения  задачи  по  определению  номинальных  величин  геометрических  параметров  симметричных  структурных  схем  механизмов  с  ЗСТК  с  диаметрами  равной  величины  //  Молодой  ученый.  —  2013.  —  №  7.  —  С.  60—65.

21.Меснянкин  М.В.,  Мерко  М.А.,  Колотов  А.В.,  Митяев  А.Е.  Условия  симметрии  механизмов  с  замкнутой  системой  тел  качения  //  Вестник  Таджикского  технического  университета.  —  2013.  —  №  3.  —  С.  29—34.