Статья опубликована в рамках: XIII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 31 октября 2013 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
РАСЧЕТ КРУГЛОЙ ПЛАСТИНЫ ПО ТЕОРИИ ТИПА КА́РМАНА–ТИМОШЕНКО–НАГДИ
Филиппова Наталья Олеговна
студент 3 курса, кафедра математического моделирования и кибернетики СыктГУ, г. Сыктывкар
E-mail: nataljafilipp5@gmail.com
Ермоленко Андрей Васильевич
научный руководитель, канд. ф.-м. наук, доцент СыктГУ, г. Сыктывкар
Решается задача о расчете напряженно-деформированного состояния круглой нормально нагруженной жестко защемленной пластины. За основу взята теория изгиба пластин типа Ка́рмана-Тимошенко-Нагди [2, 4], уточняющая квазикирхгофовскую теорию К.Ф. Черныха [6] за счет учета поперечных сдвигов по линейной теории и вариаций параметров поперечного обжатия.
Полевые уравнения типа Кармана–Тимошенко–Нагди можно записать в виде
|
|
|
(1)1 |
|
|
|
(1)2 |
|
|
|
(1)3 |
Здесь I — тождественный оператор, ![]() — оператор Лапласа, w — прогиб пластины,
— оператор Лапласа, w — прогиб пластины, ![]() — поперечная внешняя нагрузка,
— поперечная внешняя нагрузка, 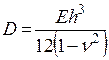 — цилиндрическая жесткость, Е — модуль Юнга,
— цилиндрическая жесткость, Е — модуль Юнга, ![]() — коэффициент Пуассона, h — толщина пластины,
— коэффициент Пуассона, h — толщина пластины,
|
|
|
(2) |
|
|
|
(3) |
Применим уравнения типа Кармана-Тимошенко-Нагди к решению задачи о расчете круглой пластины. Постановка задачи следующая. Пусть имеется круглая пластина радиуса R, толщиной h, жестко закрепленная по контуру таким образом, что реализуется осесимметричный изгиб. Пластина испытывает действие равномерной нормальной нагрузки интенсивности qn=const. Требуется определить параметры напряженно-деформированного состояния этой пластины.
Переходя к полярным координатам и учитывая осесимметричность задачи, оператор Лапласа и операторы ![]() ,
, ![]() (см. (1)) можно записать в виде (см., например, [5])
(см. (1)) можно записать в виде (см., например, [5])
|
|
|
|
|
|
|
(4)
|
Введем переменную ![]() где
где ![]() и перейдем в системе уравнений (1) к безразмерным величинам. В результате получаем, что система (1) принимает вид
и перейдем в системе уравнений (1) к безразмерным величинам. В результате получаем, что система (1) принимает вид
|
|
|
|
|
|
|
(5) |
Граничные условия жестко защемленного тангенциально свободного края примем в виде
|
|
|
|
|
|
|
|
Функции Грина для вычисления ![]() и функции напряжений
и функции напряжений ![]() совпадают и имеют вид
совпадают и имеют вид
|
|
|
Здесь ![]() — функция Хевисайда, определяемая следующим образом
— функция Хевисайда, определяемая следующим образом
|
|
|
(8) |
Решение системы (5) методом функции Грина примет вид
|
|
|
|
|
|
Для решения системы (9) применим следующую итерационную схему:
|
|
|
|
Где
|
|
|
|
Итерационная схема (10) предложена для решения поставленной задачи в рамках теории типа Кармана-Тимошенко-Нагди.
Положив ![]()
![]() и не учитывая в системе (1) третье уравнение, получим решение задачи по традиционной теории Кармана. Чтобы получить решение по теории типа Кармана-Нагди (учет только поперечного обжатия), необходимо положить
и не учитывая в системе (1) третье уравнение, получим решение задачи по традиционной теории Кармана. Чтобы получить решение по теории типа Кармана-Нагди (учет только поперечного обжатия), необходимо положить ![]() и также не учитывать третье уравнение в системе (1). И наконец, если требуется получить решение по теории типа Кармана–Тимошенко (учет только поперечных сдвигов), то полагаем
и также не учитывать третье уравнение в системе (1). И наконец, если требуется получить решение по теории типа Кармана–Тимошенко (учет только поперечных сдвигов), то полагаем ![]() ,
, ![]() .
.
На основе вычисленных w и функции напряжений ![]() находим изгибающий момент и растягивающие усилия. Момент вычисляется по следующей формуле [3]:
находим изгибающий момент и растягивающие усилия. Момент вычисляется по следующей формуле [3]:
|
|
|
|
а растягивающие усилия, соответственно, равны [3]
|
|
|
|
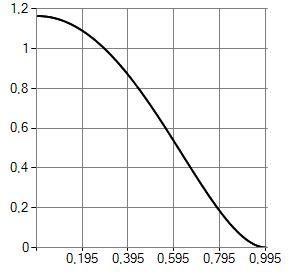
Рисунок 1. График прогиба (см)
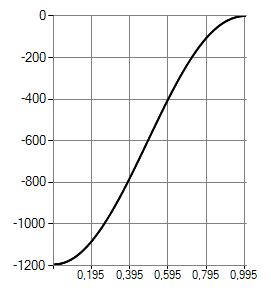
Рисунок 2. График функции напряжения (кГ/см)
В ходе работы на основе итерационной схемы (10) с использованием конечно-разностной аппроксимации [1] проводился численный эксперимент. На рисунках 1—5 показаны результаты расчета для стальной пластины по теории типа Кармана-Тимошенко-Нагди с параметрами
|
|
|
|
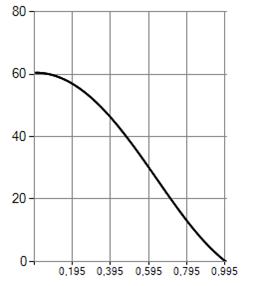
Рисунок 3. График растягивающих усилий (кГ/см)
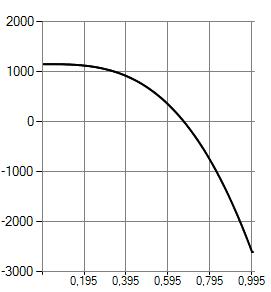
Рисунок 4. График изгибающего момента (кГ)
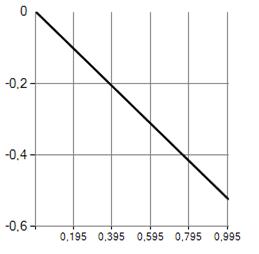
Рисунок 5. График поперечного сдвига
Получено, что выбор теории практически не сказывается на значениях параметров напряженно-деформированного состояния. Однако выбор теории оказывается существенным при решении конструктивно нелинейных задач [5].
Список литературы:
1.Власова Е.А., Зарубин В.С., Кувыркин Г.Н. Приближенные методы математической физики. М.: Изд-во МГТУ им Н.Э.Баумана, 2001. — 700 с.
2.Ермоленко А.В. Расчет круглых пластин по уточненным теориям // Вестник Сыктывкарского университета. Сер.1: Мат. Мех. Инф. — 2006. — Вып.6. — С. 79—86.
3.Михайловский Е.И. Математические модели механики упругих тел: Учебное пособие. Сыктывкар: Изд-во Сыктывкарского университета, 2004. — 324 с.
4.Михайловский Е.И., Бадокин К.В., Ермоленко А.В. Теория изгиба пластин типа Кармана без гипотез Кирхгофа // Вестник Сыктывкарского университета. Сер.1: Мат. Мех. Инф. — 1999. — Вып. 3. — С. 181—202.
5.Михайловский Е.И., Ермоленко А.В., Миронов В.В., Тулубенская Е.В. Уточненные нелинейные уравнения в неклассических задачах механики оболочек. Сыктывкар: Изд-во Сыктывкарского ун-та, 2009. — 141 с.
6.Черных К.Ф. Нелинейная теория упругости в машиностроительных расчетах. Л.: Машиностроение, 1986. — 336 с.
отправлен участнику


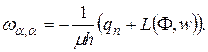
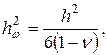
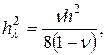
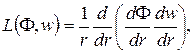
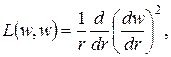
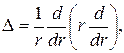
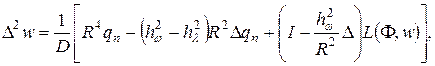
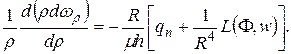
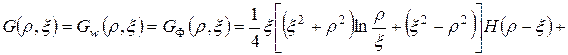
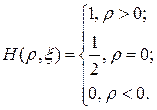
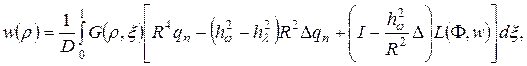
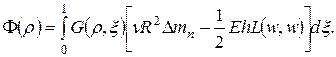
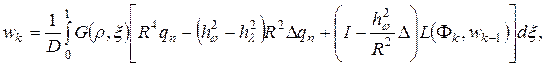
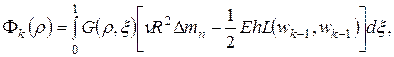
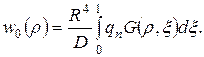
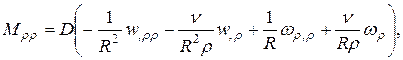
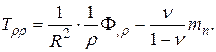
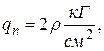
Оставить комментарий