НЕОПРЕДЕЛЕННЫЙ  ИНТЕГРАЛ  КАК  СРЕДСТВО  ФОРМИРОВАНИЯ  СПОСОБНОСТИ  ПРИНЯТИЯ  РЕШЕНИЯ  В  НЕСТАНДАРТНОЙ  СИТУАЦИИ

Коломейцева  Алина  Сергеевна

студент  1  курса  Учетно-финансового  факультета  СтГАУ,  г.  Ставрополь

E-mail:  Kolomeitsva@yandex.ru

Плаксицкая  Ольга  Геннадьевна

студент  1  курса  Учетно-финансового  факультета  СтГАУ,  г.  Ставрополь

E-mail:  plaksic-dqa@yndex.ru

Невидомская  Ирина  Алексеевна

научный  руководитель,  ассистент  кафедры  математики  СтГАУ,  г.  Ставрополь

Одним  из  основных  понятий  математики,  которое  используется  для  решения  многих  прикладных  математических  задач,  является  неопределённый  интеграл.  Математическая  операция  нахождения  неопределённого  интеграла  для  данной  функции  f(x)  имеет  в  своей  основе  понятие  первообразной  этой  функции.  Под  первообразной  будем  понимать  функцию  F(x),  которая  дифференцируема  на  промежутке  и  для  которой  выполняется  равенство  F′(x)  =  f(x).

Первообразная  данной  функции  обладает  свойством  «неопределённости»  в  том  смысле,  что  если  F(x)  первообразная  для  f(x),  то  любая  другая  первообразная  Ф(x)  может  быть  представлена  в  виде  Ф(x)  =  F(x)  +  С,  где  С  —  некоторое  число,  т.  е.  множество  функций  F(x)  +  С  образует  семейство  первообразных  для  функции  f(x)  [4,  c.  368].

В  вузовском  курсе  математики  неопределённый  интеграл  изучается  не  только  для  того,  чтобы  освоить  механизм  решения  прикладных  задач,  но  и  для  того,  чтобы  развивать  сообразительность,  логику  мышления  и  т.  п. 

Умение  находить  неопределённые  интегралы  расценивается  как  способность  глубоко  и  целенаправленно  мыслить,  строить  алгоритмы,  решать  трудные,  «осложнённые  неопределённостью»  задачи. 

Предлагая  найти  неопределённый  интеграл,  преподаватель  не  только  проверяет  знание  студентов  стандартных  математических  формул,  которые  являются  первичными  и  необходимыми,  но  и  способность  мыслить. 

Это  равносильно  тому,  как,  например,  при  приёме  на  работу  соискателю  предлагают  (в  качестве  испытания)  разрешить  нестандартную  ситуацию  или,  обучая  военнослужащих,  оперативных  работников  милиции  и  т.  п.,  «дают  вводную»  и  оценивают  дальнейшие  действия. 

Понятие  интеграла  тесно  связана  с  задачами  нахождения  квадратур  или  задачами  вычисления  площадей  плоских  фигур.  Символ  ò  был  введен  Лейбницем  в  1675  г.,  который  являлся изменением  латинской  буквы  S  .Самo  слoвo  «интеграл»  ввел  Я.  Бернулли  в  1690  г.,  а  в  1696  г.  появилось  название  новой  ветви  математики  —  интегральное  исчисление  (calculus  integralis.  Другие  теpмины,  которые  в  настоящее  время  относятся  к  неопределенному  исчислению,  появились  гораздо  позднее.  Например,  понятие  первообразной  функции  было  введено  вместо  ранее  употребляемого  названия  «примитивная  функция»  [4,  c.  382].

Многие  достижения  математикoв  Древней  Греции  в  решении  задач  на  нахождения  квадратур  или  вычисления  площадей  плоских  фигуp,  а  также  кубатур  или  вычисления  объемов  тел  связаны  с  применением  метoда  исчерпывания,  которые  были  предложены  Евдоксoм  Книдским  (408—355  до  н.  э.).  Метод  Евдокса  усовершенствовал  Архимед.  С  помощью  этого  метoда  он  дал  оценку  числа  p  (3.10/71<p<3.1/7),  нашел  объемы  шаpа  и  эллипсoида,  площадь  сегмента  параболы  и  т.  д.

Однако  перед  учеными  стаяла  задача  выделить  общие  идеи,  лежащие  в  основе  решения  многих  частных  задач,  а  также  установить  связь  операций  дифференцирования  и  интегрирования,  дающую  общий  алгоритм.  Это  независимо  друг  от  друга  сделали  Ньютоном  и  Лейбницем,  тем  самым  окончательно  было  сформулирован  общий  метод,  под  которым  понималось  дифференциальное  и  интегральное  исчисление  [4,  c.  383].

Пример:  Функция  является  первообразной  для  на  (–∞,+∞),  так  как  для  любого  x  имеем  .  Для  одной  и  той  же  функции  существует  бесконечное  множество  первообразных.  Например,  для    первообразными  на  (-∞,+∞)  являются  также  функции  ,  и  вообще    ,  где      —  произвольное  число,  поскольку  для  любого  x  [2,  c.  263].

Основным  методом  нахождения  первообразной  функции  является  непосредственное  интегрирование  с  использованием  таблицы  первообразных  и  свойств  неопределенного  интеграла.  Все  другие  методы  используются  лишь  для  приведения  исходного  интеграла  к  табличному  виду.

Пример:  Найдите  множество  первообразных  функции

Решение: 

Запишем  функцию  в  виде 

Так  как  интеграл  суммы  функций  равен  сумме  интегралов,  то

Числовой  коэффициент  можно  вынести  за  знак  интеграла:

Первый  из  интегралов  приведен  к  табличному  виду,  поэтому  из  таблицы  первообразных  для  показательной  функции  имеем: 

Для  нахождения  второго  интеграла  воспользуемся  таблицей  первообразных  для  степенной  функции    и  правилом 

.

То  есть, 

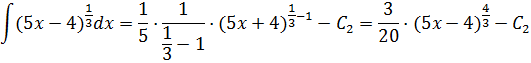
Следовательно, 

  ,

где:    [3,  c.  24].

Интегрирование  методом  подстановки  заключается  в  том,  что  вводят  новую  переменную,  выражают  подынтегральную  функцию  через  эту  переменную,  в  результате  приходят  к  табличному  (или  более  простому)  виду  интеграла.

Пример:  Найти  неопределенный  интеграл 

Решение: 

Введем  новую  переменную  . 

Выразим  x  через  z:

Выполняем  подстановку  полученных  выражений  в  исходный  интеграл:

=  2

Из  таблицы  первообразных  имеем: 

Осталось  вернуться  к  исходной  переменной  х: 

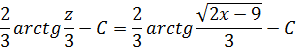
Ответ:  [3,  c.  27].

Интегрирование  по  частям  основано  на  представлении  подынтегрального  выражения  в  виде  произведения    и  последующем  применении  формулы  .  Этот  метод  является  очень  мощным  инструментом  интегрирования.  В  зависимости  от  подынтегральной  функции,  метод  интегрирования  по  частям  иногда  приходится  применять  несколько  раз  подряд  до  получения  результата.  Для  примера  найдем  множество  первообразных  функции  арктангенс  [1,  c.  187].

Пример:  Вычислить  неопределенный  интеграл  .

Решение:

Пусть  ,  тогда  ; 

Следует  отметить,  что  при  нахождении  функции  v(x)  не  прибавляют  произвольную  постоянную  С.

Теперь  применяем  формулу  интегрирования  по  частям: 

Последний  интеграл  вычислим  по  методу  подведения  под  знак  дифференциала.

Так  как  ,  то  .  Поэтому 

.

Следовательно,

, 

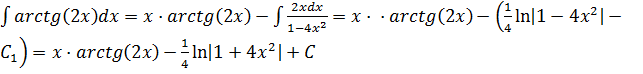где:  .

Ответ:  [3,  c.  30].

Таким  образом,  освоение  методов  интегрирования  приравнивается  к  способности  нахождения  выхода  из  ситуации,  осложненной  неопределённостями.  На  современном  этапе  развития  общества  такую  способность  специалистов  называют  компетентностью,  без  которой  очень  трудно  работать  в  условиях  рыночной  экономики.

Список  литературы:

1.Задачи  студенческих  олимпиад  по  математике:  Пособие  для  студентов  вузов/  Садовничий  В.А.,  Подколзин  А.С.  —  2-е  изд.,  стереотип.  —  М.:  Дрофа,  2009.  —  208  с.:  ил.

2.Демидович  Б.П.  Сборник  задач  и  упражнений  по  математическому  анализу./СПб:  Мифрил,  2005.  —  489  с.

3.Мамаев  И.И.,  Родина  Е.В.,  Невидомская  И.А.  Неопределенный  интеграл.  —  Методические  указания  для  студентов  аграрных  вузов.  —  Ставрополь.  —  2013.  —  36  с.

4.Математика.  Большой  энциклопедический  словарь.  /Под  ред.  Прохорова  Ю.В.  —  3-е  изд.  —  М.:  «Большая  Российская  энциклопедия»,  2009.  —  848  с.:  ил.