РАСПОЗНАВАНИЕ СИГНАЛОВ ПРИ НАЛИЧИИ ПОМЕХ С ИСПОЛЬЗОВАНИЕМ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ

Корнюшина Елизавета Юрьевна

студент 4 курса, кафедра системы автоматического управления Калужский филиал МГТУ им. Н.Э. Баумана

Е-mail: liza.kornyushina@gmail.ru

Степанов Сергей Евгеньевич

научный руководитель, канд. физ.-мат. наук, доцент, Калужский филиал МГТУ им. Н.Э. Баумана

Существует достаточно большой круг задач, связанных с распознаванием сигналов, являющихся носителем информации о состоянии объектов или процессов. Но эти сигналы, часто имеют сложную структуру и искажены влиянием случайных составляющих, помех. Для анализа таких сигналов требуется использовать методы, позволяющие выявить их характерные особенности.

К числу методов исследования структуры таких сигналов относится вейвлет-преобразование.

Вейвлетное преобразование сигналов является обобщением спектрального анализа, типичный представитель которого — классическое преобразование Фурье.

Вейвлеты — это обобщенное название семейств математических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени. Вейвлет-преобразования рассматривают анализируемые временные функции в терминах колебаний, локализованных по времени и частоте. Как правило, вейвлет-преобразования подразделяют на дискретное и непрерывное [1].

Базис собственных функций, по которому проводится вейвлетное разложение сигналов, обладает многими специфическими свойствами и возможностями. Вейвлетные функции базиса позволяют сконцентрировать внимание на тех или иных локальных особенностях анализируемых процессов.

Одна из главных особенностей вейвлетного представления сигналов на различных уровнях декомпозиции (разложения) заключается в разделении функций приближения к сигналу на две группы: аппроксимирующую — грубую, с достаточно медленной временной динамикой изменений, и детализирующую — с локальной и быстрой динамикой изменений на фоне плавной динамики, с последующим их дроблением и детализацией на других уровнях декомпозиции сигналов. Это возможно как во временной, так и в частотной областях представления сигналов вейвлетами [3].

Основной целью работы является распознавание сигналов при наличии помех («шумов») с использованием вейвлет-преобразования.

В данной работе проведен вычислительный эксперимент, в ходе которого планируется выявить возможности распознавания сигнала, содержащего белый шум с нулевым математическим ожиданием и заданной дисперсией в дискретном представлении этой случайной составляющей.

Причины возникновения шума могут быть различными: шумы измерительной аппаратуры; помехи при передаче по каналам связи; неточные условия измерения сигнала и т. д.

В качестве анализируемых образцов были выбраны сигналы: 1. имеющий форму полуокружности, 2. имеющий, треугольную форму. Два сигнала имеют одинаковые по величине значения в точке максимума и «близкие» по своей форме (Рисунок 1).

Рисунок 1. Сигнал в форме полуокружности и сигнал в форме треугольника

Предположим, что измеренное значение описывается выражением вида:

где:  — точное значения функции в точке ,а

 — погрешность измерения в данной точке.

Погрешностью измерений в данной точке является белый Гауссовский шум, с математическим ожиданием M[x]=0 и дисперсиеей σ²[x]=A, с нормальным законом распределения.

Необходимо определить при какой дисперсии случайной составляющей A сигналы становятся статистически неразличимы, то есть при какой дисперсии случайной составляющуй происходит увеличение соотношения сигнал/шум и выделение слабого сигнана на фоне сильных внешних помех, становится затруднительным.

Для это было проведено вычисление относительных погрешностей измерения кругового и треугольного сигналов по следующей формуле:

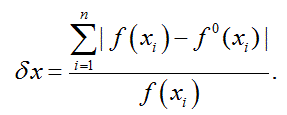
Сигналы становятся статистически неразличимыми при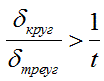

где: t- распределение Стьюдента при доверительной вероятности 95 % и достаточного большого числа наблюдений (N>100).

При доверительной вероятности 95 % и числе наблюдений N = 120, значение t = 1,98 [2].

То есть при величине большей чем  сигналы становятся статистически неразличимы.

Для исследуемых сигналов было найдено такое значение дисперсии случайной составляющей сигнала, при которой 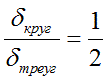. Сигналы находятся на грани статистической неразличимости. (Рисунок 2. и Рисунок 3.)

Рисунок 2. Круговой сигнал с дисперсией шума 2,25

Рисунок 3. Треугольный сигнал с дисперсией шума 2.25

В ходе вычислительного эксперимента было выявлено соотношение «сигнал/шум», при котором сигналы стали статистически неразличимы. Это позволяет разработать алгоритмы, позволяющие найти оптимальное решение задачи анализа изображений, звуковых сигналов, результатов дактилоскопической экспертизы, включающая их обработку.

Список литературы:

1.     Новиков Л.В. Основы вейвлет-анализа сигналов: Учебное пособие. — СПб, ИАнП РАН, 1999, 152 с.

2.     Пугачев В.С. Теория вероятностей и математическая статистика. М.: Наука, 1979. — 496 с.

3.     Смоленцев Н.К. Основные теории вейвлетов. Вейвлеты в MATLAB. М.: ДМК Пресс, 2005. — 304 с.