УЧЕТ НЕЛИНЕЙНОСТИ СВОЙСТВ МАТЕРИАЛОВ ПРИ РАСЧЕТЕ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ

Рамазанова Гульнара Алфатовна

студент 1 курса магистратуры, кафедра строительных конструкций БрГУ, г. Братск

Е-mail: Gulnara_23-1990@mail.ru

Коваленко Галина Владимировна

научный руководитель, канд. техн. наук, профессор БрГУ, г. Братск

Важной особенностью реальных материалов является нелинейный характер зависимости между напряжением и деформацией. Учет таких особенностей деформирования материалов конструкций в расчете позволяет приблизить теоретические прогнозы к реальному их поведению.

В практике проектирования железобетонных конструкций принято различать физическую, геометрическую и конструктивную нелинейности.

Для полного анализа напряженно-деформированного состояния конструкции следует учитывать все три вида нелинейностей. Физическая нелинейность обусловлена учетом в расчете нелинейной зависимости между компонентами обобщенных напряжений и деформаций  и характеризует работу материала конструкции в упругопластической области.

Для упрощения решения задач с физической нелинейностью широко используется гипотеза о нелинейно-упругом материале, согласно которой зависимости между напряжениями и деформациями при нагрузке и разгрузке тождественны. Основную предпосылку нелинейной теории упругости можно сформулировать следующим образом: при сложном напряженном состоянии зависимость между интенсивностями напряжений и деформаций для каждой точки тела принимается такой же, как зависимость между напряжениями и деформациями при простом растяжении того же тела [2].

Расчет за пределом упругой работы конструкций имеет целью, насколько это возможно, уменьшить расход материала, создаваемый расчетом по упругой стадии, получив существенную экономию. Поэтому строительные нормы и правила уже требуют, чтобы расчетные схемы конструкций учитывали физическую нелинейность и пластические свойства материалов.

В 2003 г. взамен СНиП 2.03.01-84* были утверждены и введены в действие новые Нормы проектирования бетонных и железобетонных конструкций — СНиП 52-01-2003.

Существенные изменения коснулись деформативных характеристик материалов. Введены новые нормативные понятия — «диаграммы состояния» бетона (т. е. диаграммы сжатия) и арматуры (диаграмма растяжения), которых в старых Нормах не было, поскольку отсутствовала сама надобность в них. В общем случае диаграммы состояния имеют криволинейный характер, но для практических расчетов могут быть использованы более простые. На основании действующих норм проектирования диаграмма растяжения арматуры представлена как двухлинейная, то есть как идеализированная диаграмма Прандтля, согласно которой материал деформируется по закону Гука до предела текучести, а затем течет вплоть до разрыва (рисунок 1б). Диаграмма сжатия бетона представлена трехлинейной, более близкой к реальной (рисунок 1в).

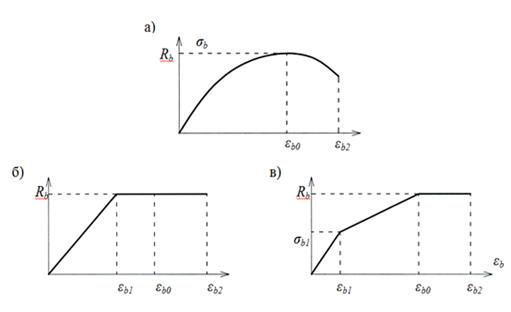
а — реальная; б — двухлинейная; в v трехлинейная.

Рисунок 1. — Диаграмма сжатия бетона

а — реальная; б — идеализированная диаграмма Прандтля.

Рисунок 2. — Диаграмма растяжения арматуры

Для полного анализа напряженно-деформированного состояния конструкций с целью их последующей оптимизации необходимо выбрать оптимальную расчетную модель.

В настоящее время выдвинуто немало предложений по построению диаграмм деформирования бетона и арматуры, а также способы их учета при расчетах конструкций. Наибольший интерес представляют такие способы, которые позволяют единообразно описывать диаграммы деформирования бетона и арматуры.

В работах [1,4] рассматривается дискретная модель по нелинейно-деформационной модели. Учет физической нелинейности производится путем математического описания диаграмм деформирования бетона и арматуры, также применение шагово-итерационного метода, который реализует способ упругих решений.

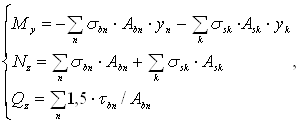
Решение нелинейной задачи получается в виде последовательности решений линейных задач, которые приводят к результату. Условия равновесия внешних и внутренних сил [1] записывается в виде:

  (1)

где: M_y  — изгибающий момент в направлении оси Y,

N_z — продольная сила в направлении оси Z,

Q_y — поперечная сила в направлении оси Y.

Учитывая, что напряжения в дискретных элементах бетона и арматуры определяются из диаграмм деформирования материалов, получается:

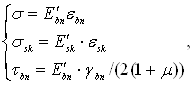 (2)

где: E'_bn, E'_sk  — секущие модули деформаций бетона и арматуры, зависящие от расположения элементарных участков в сечении и уровня нагружения;

ε_bn, ε_sk — продольные относительные деформации участков

A_bn и A_sk, определяемые по зависимостям, исходя из гипотезы плоских сечений:

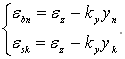 (3)

где: ε_z  — деформации вдоль продольной координационной оси элемента Z;

k_y — кривизна элемента в плоскости XY.

В работе [3] рассмотрен метод расчета конструкций со смешанным армированием, в основу которого положена дискретная модель фактического сечения конструкции: поперечное сечение любой формы разбивается на n-ое число элементарных участков бетона и k-ое число участков арматуры, равное числу продольных стержней арматуры. Физическая нелинейность учитывается применением полных диаграмм деформирования материалов, аппроксимированных по способу секущих модулей.

Расчет выполняется шагово-итерационным способом с использованием методики приращений, т. е. на каждом шаге нагружение статической нагрузкой и вызываемое им напряженно-деформированное состояние конструкции рассматривается относительно ее напряженного состояния на предыдущем этапе нагружения. Условие равнове­сия внешних и внутренних сил на любом этапе загружения записыва­ется в виде {F}= [R({F},S)]*{U({F},S)}, где {F} — вектор-столбец внешних сил, принимаемый в зависимости от схемы загружения; {U({F},S)} — вектор-столбец деформаций, являющийся функцией внешних сил {F} и геометрических параметров сечения S; [R({F},S)] — матрица жесткости для нормального сечения, являющейся функцией {F} и S.

Расчет имеет компактную универсальную и удобную для реализации на ЭВМ математическую форму.

Данная модель применима только к расчету нормальных сечений изгибаемых элементов в зоне с максимальным изгибающим моментом, поскольку не учитывает влияние поперечной силы.

Расчетные модели с использованием диаграмм деформирования материалов представляют собой универсальный способ расчета любых типов железобетонных конструкций, подвергающихся воздействию изгибающих моментов и продольных сил. На основе данных моделей могут быть получены полные диаграммы состояния элемента железобетонной конструкции, связывающие усилия (моменты и продольные силы) с перемещениями (кривизной, удлинением и укорочением).

Следовательно, учет реальных свойств бетона и арматуры приближает теоретические прогнозы к реальному поведению конструкций под нагрузкой, что дает возможность выявлять резервы снижения их материалоемкости, обеспечивая тем самым существенную экономию. Также деформационная модель позволяет достаточно точно решить задачу подбора ненапрягаемой арматуры в конструкциях со смешанным армированием при заданном классе напрягаемой с учетом разных модулей упругости в смешанной арматуре и ее различного расположения по высоте сечения [3].

Список литературы:

1.Карпенко Н.И. Общие модели механики железобетона / Н.И. Карпенко. — М.: Стройиздат, 1996. — 416 с.

2.Рудых О.Л. Введение в нелинейную строительную механику: учеб. пособие / О.Л. Рудых, Г.П. Соколов, В.Л. Пахомов; под ред. О.Л. Рудых. — М.: Издательство ассоциации строительных вузов, 1998. — 103 с.: ил.

3.Тамразян А.Г., Дудина И.В. Учет нелинейных свойств мате­риалов при расчете конструкций со смешанным армированием// Бетон и железобетон, 2003, № 2. — с. 11—12.

4.Kovalenko G.V. Chance models and estimators of primary reability of constructions with mixed rein for cement/ G.V. Kovalenko, I.V. Dudina, E.V. Nester// European Science and Technology [Text]: materials of the international research and practice conference, Vol. I. Wiesbaden, January 31^st, 2012 / publishing office «Bildungszentrum Rodnike. V. ». — c. Wiesbaden, Germany, 2012. — 820 p. — C. 237—243.