ОРГАНИЗАЦИЯ ПРОЦЕДУРЫ ПРОГНОЗИРОВАНИЯ КОНЦЕНТРАЦИЙ ВРЕДНЫХ ВЕЩЕСТВ В ВОЗДУШНОЙ СРЕДЕ ПО СТАТИСТИЧЕСКИМ ДАННЫМ

Мещерякова Юлия Александровна

магистрант 2 курса, кафедра высшей математики ЕГФ, ЮФУ, г. Таганрог

E-mail: life-super@yandex.ru

Гадельшин Валерий Камельянович

научный руководитель, канд. тех. наук, доцент кафедры ВМ, ЕГФ, ЮФУ, г. Таганрог

Одной из главных экологических проблем в городах является высокий уровень загрязнения воздушной среды. Основные источники выбросов вредных, загрязняющих атмосферу веществ — автотранспорт и промышленные предприятия. Например, в 2009 году на долю автотранспорта в г. Таганроге приходилось 79,1 % от общего объема выбросов загрязняющих веществ, а по данным УГИБДД ГУВД по Ростовской области количество автомобилей в Таганроге с 35 тысяч в 2001 году к 2010 году увеличилось до 61000 единиц. Вблизи транспортных магистралей с интенсивным движением при неблагоприятных метеоусловиях и заторах содержание вредных примесей в воздухе значительно превышает допустимый уровень.

Сложность проведения регулярных трудоемких натурных экспериментов для оперативной и долговременной оценки и прогнозирование состояния воздушной среды приводит к необходимости применения вычислительных экспериментов методами математического моделирования и обработки статистических данных.

В данной работе предлагается метод и программный комплекс, позволяющие на основе статистических данных по выбросам загрязняющих веществ автотранспортом в экологически проблемных местах г. Таганрога, выполнять оперативный прогноз концентрации вредных веществ в атмосфере при заданных метеорологических условиях и составе транспортного потока.

Для оперативного прогноза концентрации загрязняющих веществ разработан алгоритм, состоящий из следующих процедур: создание базы данных, выборка данных из БД по точечным и интервальным запросам; выявление решающих параметров; нормализация данных; классификация замеров по месту и метеоусловиям; группирование замеров на основе алгоритмов кластеризации; выявление принадлежности исходной точки к тому или иному кластеру; формирование прогноза концентрации веществ, характерных для данной группы замеров.

Исходными данными являются замеры концентрации загрязняющих веществ в воздухе, сведения по составу автомобилей в потоке, метеоусловия с привязкой к месту и времени проводимых измерений, выполняемых ФГУЗ «Центром гигиены и эпидемиологии» в г. Таганроге в течение более десяти лет. Они позволяют характеризовать обстановку в городе в целом, а также служат для всестороннего анализа оценок и прогнозов. Пример исходных данных приведен в таблице 1.

Таблица 1.

На основе анализа исходных данных и различных СУБД для поддержки  программного комплекса используется: Microsoft SQL Server 2008 R2 Express (для базы данных) и Microsoft Visual Studio Express 2010 (для программного продукта) (см. рисунок 1).

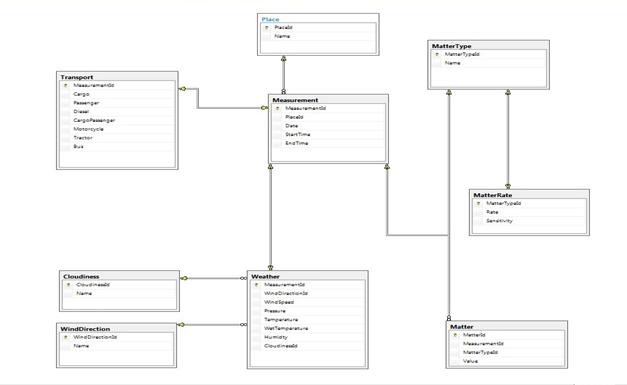
Рисунок 1. Состав и структура базы данных

Импорт данных из БД в программу осуществляется с помощью стандартных функций ADO.NET. Решающими параметрами выбраны: место проводимых измерений (на концентрацию вредных веществ в атмосфере имеет влияние рельеф местности и застройка); тип погоды; температура; давление; скорость ветра; количество машин по типам.

Общий вклад загрязняющих веществ, вносимых каждым элементом, определяется расчетным путем с использованием коэффициентов, полученных с применением методики, изложенной в [9, с. 15]. При разных значениях коэффициентов проведена верификация базы данных, и выбраны те, для которых получено наименьшее расхождение между исходными и прогнозируемыми значениями концентраций. Подобная практика использования коэффициентов встречается в работах [4, с. 193], в которых оценивалось влияние каждого метеопараметра на степень загрязнения, и полученные результаты использовали для составления прогноза загрязнения.

После нормализации данные представляются в удобном для использования виде.

Результатом нормализации является модель данных, которую легко поддерживать, и она не содержит неопределенностей в данных и повторений. В данном случае, все замеры для типов автомобилей находятся на некотором отрезке [a,b], который нормализуется в [0,1], и значение x [a,b] вычисляется по формуле , [0,1].

Кластерный анализ — задача разбиения множества замеров на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов (замеров), а объекты разных кластеров существенно отличались. Кластер — группа элементов, характеризуемых общим свойством, главная цель кластерного анализа — нахождение групп схожих объектов в выборке. Решение задачи кластеризации зависит от параметров кластеризации: критерия «похожести» элементов (после нормализации данные-замеры представляются в виде точек в евклидовом пространстве с набором координат-параметров, критерий похожести — это сходство координат, т. е. насколько близко в пространстве находятся точки); от используемой метрики d, измеряющей расстояние между векторами-образами (пространство является евклидовым, метрику вычисляем стандартно); от оцениваемого числа кластеров (оптимальное число кластеров ориентировочно предполагается равным 6, что основывается на исходном количестве замеров); нахождение нетипичных элементов (т. е. элементов, не попадающих ни в один из кластеров, имеет значение при формировании кластеров из данных БД, поскольку замеры неоднородны).

Задача кластеризации формулируется следующим образом. Дана обучающая выборка — множество всех замеров Ω = {x₁,…,x_n}. Требуется найти  такую функцию кластеризации f , которая  каждой точке (замер с решающими параметрами) x ∈ Ω ставила бы в однозначное соответствие некоторый элемент — метку z ∈ Z из множества меток Z = {z₁,…,z_n}[6, с. 38]. Обучающая выборка, используя один из алгоритмов кластеризации, разделяется на необходимые подгруппы внутри уже полученных классов по месту измерения и подклассов типа погоды.

Анализ алгоритмов кластеризации показывает, что для решения данной задачи рационально использовать максиминный алгоритм, поскольку он прост для реализации, обучается быстрее и не чувствителен к размерности (по сравнению с алгоритмом k-means). На рисунке 2 приведен пример кластеризации.

1.  В качестве первого центра кластера выбирается элемент c₁ = x₁ .

2.  Вторым центром кластера выбирается тот элемент c₂ = , который находится на наибольшем расстоянии от c₁, т. е.  .

3.  Предположим, что выбраны k — центров C^(k) ={c₁,…,c_k} кластеров. В качестве  очередного (k+1) — го центра кластера выбирается тот элемент  , который  находится на наибольшем расстоянии от ближайшего из центров c₁,…,c_k (рис. 2), т. е.

4.  .

5.  Проверяется условие останова — мы установили число кластеров равное 6, как оптимальное для количества замеров в БД.

Рисунок 2. Определение центров кластеров и относящихся к ним элементов. c₁ , с₂, c₃ — центры кластеров

Данные о концентрации примеси и относящиеся к ним ситуации группируются так, чтобы выделить 6 групп (кластеров) значений потока, причем сначала формируются группы по месту замера (количество — 6), затем подгруппы по типу погоды (количество — 3 для каждого класса). Пусть замеры описываются векторами-характеристиками , i=1,2,…,n. Для группы, состоящей из M_j ситуаций, определяются центр тяжести i-й характеристики X_i и средняя дисперсия.

Например, для 1 кластера

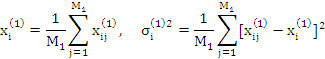
Для каждой из групп выделяется по одному вектору-характеристике таким образом, чтобы эти векторы имели наиболее низкие степени близости между собой. При разбиении совокупности на два кластера (m=2) выбирается два вектора-представителя с минимальной близостью между собой, т. е. определяются номера , из условия: , где – числа характеризующие подобие, определяются формулой:

При m=3 к двум уже выбранным векторам  добавляется третий вектор , где  выбирается из условия

которое позволяет выбрать третий вектор с наименьшей степенью близости совокупности первых двух.

  Если уже выбраны m-1 векторов , то вектор  выбирается из оставшихся векторов-характеристик по условию

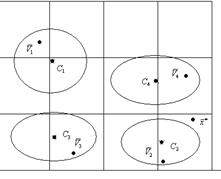
Рисунок 3. Кластеры

Распределение на кластеры заканчивается, если

 ,

где  — достаточно малое число.

Если считать, что среди проведенных наблюдений зафиксированы все возможные метеорологические ситуации, то прогноз методом распознавания образов связан с выбором из множества кластеров таких ситуаций (кластеров), которые близки к «прогнозируемой». В основе применения метода распознавания образов лежит представление о том, что большие концентрации примесей связаны с вполне определенными метеорологическими ситуациями и характером предшествующего загрязнения воздуха. Конкретный комплекс характеристик используется для определения группы, к которой можно отнести прогнозируемую ситуацию (процедура «обучения»). Для каждой конкретной ситуации, характеризуемой в фазовом пространстве точкой y с координатами , определяется расстояние до центра тяжести кластера.

Аналогично находится расстояние до остальных групп.

Ситуация y относится к той группе, расстояние до которой минимально. Далее считается средняя концентрация каждого вещества, характерного для данного кластера:

,

где n — количество элементов в кластере, x_j — концентрация вещества.

Чтобы убедиться в том, что программа работает корректно, проведен ряд вычислительных экспериментов. Из БД случайным образом извлекается замер, который задается в качестве прогнозируемой ситуации, и далее сравниваются прогнозируемая концентрация и исходные данные.

Пример:

В качестве прогнозируемой ситуации вводится существующий замер, удаленный из базы (рис. 4). Работа программы отражена на рисунках 4—6.

Рисунок 4. Параметры прогнозируемой ситуации

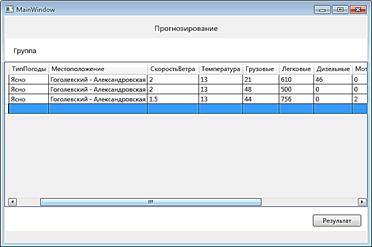
Рисунок 5. Кластер, к которому отнесена прогнозируемая ситуация

Рисунок 6. Прогнозируемая концентрация веществ для заданных условий

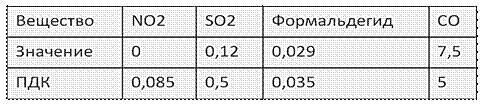
Рисунок 7. Исходные данные по концентрации вредных веществ при заданных условиях

На рисунках 6 и 7 результаты для сравнения: прогнозируемая концентрация близка к действительной. Проверка показала, что 14 из 15 замеров совпали по оценке (отклонение до 3 %) с тем прогнозом, что рассчитан программным комплексом, а интервал разброса для оставшихся замеров составляет от 3 % до 10 %, что показывает достаточно успешную работу программного комплекса.

На основе полученной прогнозированием концентрации можно контролировать ситуацию загрязнения на автотранспортных магистралях.

Программный комплекс позволяет делать прогноз концентрации вредных веществ в воздушной среде в городских условиях, и может использоваться в экологических службах, в частности в «Центре гигиены и эпидемиологии в Ростовской области».

Для повышения эффективности работы программного комплекса в дальнейшем предполагается добавление в него процедуры «переобучения». Приведенные в данной работе результаты, подтверждают возможность построения таких схем на базе методов распознавания образов.

Список литературы:

1.Авдеева Т.П. Расчет выброса загрязняющих вещест»: Учеб. пособие. — Пенза, 1997. — 87 с.

2.Агаев Т.Б., Беккер А.А. Охрана и контроль загрязнения природной среды. — Л.: Гидрометеоиздат, 1989. — 67 с.

3.Белов П.Н., Семенченко Б.А. Метеорологические аспекты охраны природной среды. Изд-во МГУ, 1984. — 96 с.

4.Берлянд М.Е. Прогноз и регулирование загрязнения атмосферы. — Л: Гидрометеоиздат, 1985 — 271 с.

5.Берлянд М.Е. Современные проблемы атмосферной диффузии и загрязнения атмосферы. — Л: Гидрометеоиздат, 1975. — 448 с.

6.Броневич А.Г., Лепский А.Е. Математические методы распознавания образов. Курс лекций. — Таганрог: Изд-во ТТИ ЮФУ, 2009. — 155 с.

7.Генихович Е.Л., Гущин В.А., Сонькин Л.Р. О возможности прогноза загрязнения городского воздуха методом распознавания образов. Труды ГГО, 1969, вып. 238.

8.Метеорологические аспекты загрязнения атмосферы. Сб. докладов на международном симпозиуме в Ленинграде. Под ред. Берлянда М.Е., — Л.: Гидрометеоиздат, 1971. — 51 с.

9.Методика расчетов выбросов в атмосферу загрязняющих веществ автотранспортом на городских магистралях. — М.: НИИАТ, 1997. — 54 с.

10.Назаров И.М., Николаев А.Н., Фридман Ш.Д. Основы дистанционных методов мониторинга загрязнения природной среды. — Л.: Гидрометеоиздат. 1983. — 213 с.

11.Руководящий документ. Охрана природы. Атмосфера. Руководство по прогнозу загрязнения воздуха. РД 52.04.306-92