Статья опубликована в рамках: V Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 22 октября 2012 г.)
Наука: Технические науки
Секция: Материаловедение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
РЕАЛИЗАЦИЯ ЧИСТОГО И ПРОСТОГО СДВИГА В СЛУЧАЕ УПРУГОЙ БИМОДУЛЬНОЙ СРЕДЫ
Андрианов Иван Константинович
студент 6 курса, кафедра механики и анализа конструкций и процессов, КнАГТУ, г. Комсомольск-на-Амуре,
E-mail: ivan_andrianov_90@mail.ru.
Олейников Александр Иванович
научный руководитель, д-р. физ. мат наук, профессор КнАГТУ,
г. Комсомольск-на-Амуре
Исследования упругих свойств многих материалов указывают на отличие в их поведении от линейного закона Гука при малых деформациях. Материалы, по-разному сопротивляющиеся растяжению и сжатию называются бимодульными [3, c. 17]. Свойство бимодульности характеризуется существенным расхождением значений модуля Юнга и коэффициента Пуассона при растяжении ![]() и при сжатии
и при сжатии ![]() [4, с. 18] .
[4, с. 18] .
В основе чувствительности материала к виду напряженного состояния могут лежать соответствующие возмущения его микроструктуры. Такие возмущения в основном происходят в системе микроповреждений материала и представляют собой, например, изменение формы и размеров дефектов, потерю устойчивости элементов микроструктуры, а также реализацию или, наоборот, устранение действия имеющихся локальных нарушений связности и сплошности. В расчетах напряженно-деформированного состояния бимодульных материалов, свойством бимодульности часто пренебрегают и рассматривают обыкновенную линейно-упругую модель сплошной среды, что может приводить к принципиальным расхождениям с экспериментальными данными.
Микронарушения обычно присущи всем неоднородным структурам, их наличие может быть следствием технологических процессов производства, получения и синтеза материала, а также природных процессов его образования, приложения нагрузок, пластических деформаций, взаимодействия с полями, химических и биологических процессов. Под микронарушениями можно понимать не только устойчивые трещины, поры и другие нарушения сплошности, но и локальные нарушения связности — разрезы, щели, трещины с сомкнутыми берегами.
Бимодульность установлена для многочисленных сплавов: чугуна, бронзы и стали. У стали бимодульность проявляется незначительно, различие в значениях модуля Юнга при растяжении и сжатии не более 3—5 %, у чугуна может достигать 30 % и более. Свойством бимодульности обладают некоторые конструкционные материалы, в частности, армированные и неармированные полимеры. Установлена существенная бимодульность капрона и фторопласта, а также изотропного неармированного полистирола (оргстекло) [2, c. 9].
Сильно выраженным свойством бимодульности обладает такой распространенный строительный материал, как бетон. Для некоторых видов мелкозернистого бетона модуль Юнга при растяжении в два-три раза меньше, чем при сжатии. Столь существенные различия в значениях параметров, очевидно, будут приводить к значительным расхождениям в результатах расчетов деформаций для бетона без учета его свойства бимодульности. Свойство бимодульности также характерно для грунтов и горных пород. Для различного типа гранитов модуль Юнга при сжатии превосходит модуль Юнга при растяжении до 1,5 раз, а для осадочных пород (известняки, песчаники) — до 4 раз. Таким образом, получение точной картины напряженно-деформированного состояния чрезвычайно важно и актуально при расчетах многих конструкций, строительных сооружений.
Для классического случая обобщенный закон Гука имеет следующий вид:
![]()
![]()
В случае бимодульных материалов упругие свойства будут зависеть от знаков главных напряжений. Например, при действии нормального напряжения![]() линейные деформации будут записываться следующим образом [1, c. 18]:
линейные деформации будут записываться следующим образом [1, c. 18]:


Рассмотрим случай чистого сдвига в упругом бимодульном материале, реализуемый с помощью касательного напряжения ![]() :
:
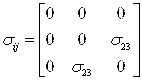
Используя закон преобразования, найдем компоненты напряжений в новой системе координат:![]()
![]()

Рисунок 1. Действующие напряжения на площадках чистого сдвига
Если положить, что данные касательные напряжения положительны, то мы приходим к выводу, что данный чистый сдвиг в исходной системе координат эквивалентен двустороннему сжатию и растяжению в новой системе координат.
![]()
![]()
Применяя формулу для всех остальных напряжений в новой системе координат, убеждаемся, что они равны нулю: σkl = 0.
При растяжении деформации удовлетворяют соотношениям: 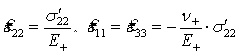 , а при сжатии:
, а при сжатии: 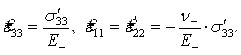
Найдем компоненты деформаций в новой системе координат:
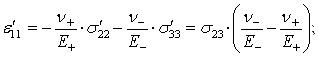

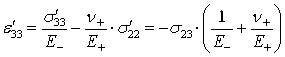
Для того чтобы найти компоненты деформаций в исходной системы координат, необходимо воспользоваться формулой перехода:
![]() где
где ![]()
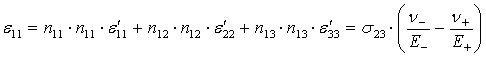

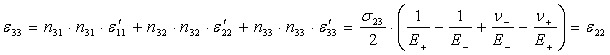
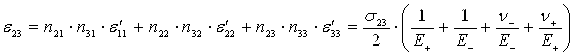

![]()
Тензор деформаций при чистом сдвиге примет следующий вид:

В результате чистого сдвига в теле возникают сдвиговые деформации, приводящие к изменению формы, и линейные деформации по всем трем направлениям, при этом ![]() . Объемная деформация отлична от нуля, следовательно при реализации чистого сдвига в бимодульной упругой среде, происходит изменение объема:
. Объемная деформация отлична от нуля, следовательно при реализации чистого сдвига в бимодульной упругой среде, происходит изменение объема: ![]()

Среднее напряжение обращается в ноль при изменении объема: ![]()
![]() . Очевидно, что для классического случая
. Очевидно, что для классического случая ![]() нулевому среднему напряжению
нулевому среднему напряжению ![]() соответствует нулевая объемная деформация
соответствует нулевая объемная деформация ![]() .
.
Интенсивность касательных напряжений определяется, как  тогда
тогда ![]() . Интенсивность сдвиговых деформаций пропорциональна действующему касательному напряжению:
. Интенсивность сдвиговых деформаций пропорциональна действующему касательному напряжению:
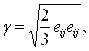
![]()

Третий инвариант девиатора тензора напряжений, отвечающий за максимальное касательное напряжение, обращается в ноль: ![]()
![]() . Третий инвариант девиатора тензора деформаций:
. Третий инвариант девиатора тензора деформаций:
![]()
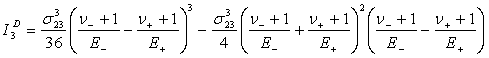
Параметры Лоде для чистого сдвига в случае бимодульной среды:



![]()
где главные деформации:
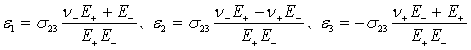
Подобие девиаторов, как видно, при чистом сдвиге нарушается, фаза их подобия отлична от нуля: ![]()
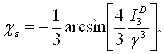
![]()
В отличие от классической теории упругости, в которой поведение тела описывается законом Гука, в теории упругости для бимодульных материалов форма закона связи деформаций с напряжениями зависит от комбинации знаков нормальных и касательных напряжений.
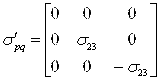
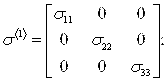
В случае же простого сдвига ![]() поведение сдвигающих напряжений остается классическим, а поведение нормальных напряжений различается, поскольку они будут отличны от нуля, их величины пропорциональны сдвигающим напряжениям. Положим, что для реализации простого сдвига напряженное состояние должно иметь следующий вид:
поведение сдвигающих напряжений остается классическим, а поведение нормальных напряжений различается, поскольку они будут отличны от нуля, их величины пропорциональны сдвигающим напряжениям. Положим, что для реализации простого сдвига напряженное состояние должно иметь следующий вид:
 где
где ![]()
Разложим задачу простого сдвига на две простые, связанные с растяжением-сжатием и чистым сдвигом:

В случае простого растяжения-сжатия деформации примут вид:

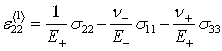
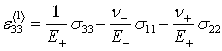
Тензор деформаций при простом растяжении-сжатии для бимодульных материалов примет следующий вид:
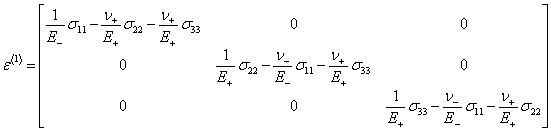
Тензор деформаций для случая чистого сдвига, полученные ранее применительно к упругой бимодульной среде:

На основе положений о линейной деформируемости и малости деформаций можем построить тензор деформаций при простом сдвиге путем сложения ![]() . Кроме того, линейные деформации при простом сдвиге отсутствуют, поэтому потребуем выполнение следующего условия:
. Кроме того, линейные деформации при простом сдвиге отсутствуют, поэтому потребуем выполнение следующего условия:
![]()
Применяя данное условие можем составить систему и разрешить ее относительно компонент нормальных напряжений:

Тензор напряжений при простом сдвиге содержит нормальные компоненты![]()
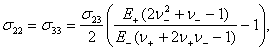 отвечающие за равномерное растяжение/сжатие и пропорциональные действующему касательному напряжению
отвечающие за равномерное растяжение/сжатие и пропорциональные действующему касательному напряжению ![]() . Видно, что для классического случая
. Видно, что для классического случая ![]() среднее напряжение, характеризующее напряженное состояние при всестороннем растяжении и сжатии будет равно нулю σ = 0.
среднее напряжение, характеризующее напряженное состояние при всестороннем растяжении и сжатии будет равно нулю σ = 0.

Рисунок 2. Простой сдвиг в случае упругого бимодульного материала
Тензор деформаций при простом сдвиге будет составлен только из сдвиговых деформаций, пропорциональных действующему сдвигающему напряжению ![]() :
: 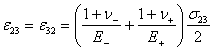 .
.
Отсюда следует, что реализация простого сдвига в случае бимодульной среды требует приложения кроме касательных напряжений еще и пропорциональных им нормальных напряжений. В результате простого сдвига в теле возникают только сдвиговые деформации, вызванные действием и касательных, и нормальных напряжений. Изменение объема при действии таких напряжений происходить не будет ![]() . Среднее напряжение будет отлично от нуля при нулевой объемной деформации:
. Среднее напряжение будет отлично от нуля при нулевой объемной деформации:

Интенсивность касательных напряжений и интенсивность сдвиговых деформаций пропорциональны действующему касательному напряжению:
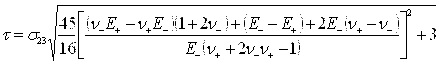

Третий инвариант девиатора тензора напряжений, отвечающий за максимальный сдвиг: 
Третий инвариант девиатора тензора деформаций: ![]()
Параметры Лоде:![]()

где главные напряжения:
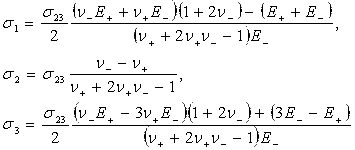
Подобие девиаторов при простом сдвиге нарушается, фаза их подобия отлична от нуля:
![]() ,
, ![]()
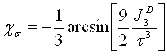
Основным недостатком принципа суперпозиции, который использовался для решения задачи чистого и простого сдвига, является отсутствие упругого потенциала, с помощью которого выражались бы напряжения и деформации в случае бимодульного материала. Таким образом, рассмотрим обратную задачу: определим напряженно-деформированное состояние при чистом и простом сдвиге, отталкиваясь от изначально-заданного упругого потенциала. Положим, что в процессе деформаций кинетическая энергия настолько мала, что ею можно пренебречь, а работа внутренних сил полностью переходит в потенциальную энергию деформации и наоборот.
Представим потенциальную энергию деформации для бимодульной среды в следующем виде: ![]() , где параметр
, где параметр ![]() является функцией инвариант тензора напряжений.
является функцией инвариант тензора напряжений.
Энергия деформаций для случая растяжения ![]() и сжатия
и сжатия ![]() будет иметь вид:
будет иметь вид:
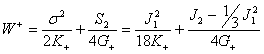 ,
, 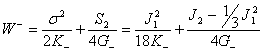
при этом ![]()
![]()
![]() .
.
Компоненты деформаций можем записать, используя закон потенциальности:
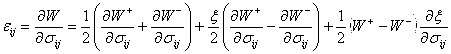
Найдем соответствующие производные по напряжениям:

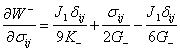
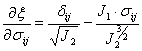
Подставим производные и получим соотношение для деформаций, выраженное через компоненты напряжений:
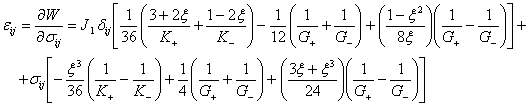
Воспользуемся полученным соотношением для описания напряженно-деформированного состояния при чистом сдвиге. Компоненты напряжений будут удовлетворять: ![]()
![]() . Учитывая, что
. Учитывая, что ![]() тензор деформаций при чистом сдвиге будет иметь вид:
тензор деформаций при чистом сдвиге будет иметь вид:

Линейные деформации пропорциональны действующему сдвигающему напряжению и одинаковы по всем трем направлениям, что соответствует равномерному объемному расширению. Сдвиговые деформации, определенные через принцип суперпозиции и с помощью упругого потенциала совпадают.
Для определения напряженно-деформированного состояния при простом сдвиге выразим компоненты напряжений через деформации для случая бимодульной среды. Потенциальная энергия деформации определяется соотношением: ![]() , где параметр
, где параметр ![]() является функцией инвариант тензора деформаций.
является функцией инвариант тензора деформаций.
![]()
![]()
Компоненты напряжений выразим, используя потенциальный закон:

Найдем производные тензорных величин:

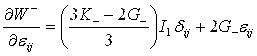

В результате получим соотношение, позволяющее определить напряжения через деформации для случая упругих бимодульных материалов:
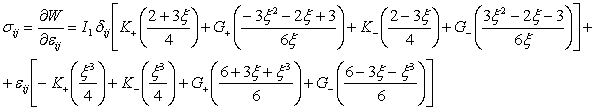
В случае простого сдвига линейные деформации отсутствуют: ![]()
![]() , тогда нормальные компоненты тензора напряжений будут пропорциональны действующему касательному напряжению и равны между собой
, тогда нормальные компоненты тензора напряжений будут пропорциональны действующему касательному напряжению и равны между собой ![]() ,
, ![]() . Тензор деформаций при простом сдвиге содержит только компоненты, отвечающие за изменение формы:
. Тензор деформаций при простом сдвиге содержит только компоненты, отвечающие за изменение формы: ![]() .
.
Таким образом, поскольку действие касательных напряжений при чистом сдвиге эквивалентно действию в главных осях растягивающего напряжения, различие секущих модулей и коэффициентов поперечной деформации при чистом растяжении и сжатии сказывается и при сдвиге. При этом, чистый сдвиг не сводится к деформациям простого сдвига, он может вызывать кроме изменения формы, также и изменение объема и приводить к нарушению пропорциональности девиаторов напряжений и деформаций. С другой стороны, и простой сдвиг в случае бимодульной упругой среды не может уже быть реализован действием одних лишь касательных напряжений, необходимо приложение и нормальных нагрузок, что влечет за собой нарушение подобия девиаторов.
Список литературы:
1.Амбарцумян С.А. Разномодульная теория упругости. — М.: Наука, 1982. — 320 с.
2.Мясников В.П., Олейников А.И. Основы механики гетерогенно-сопротивляющихся сред. Владивосток: Дальнаука, 2007. — 171 с.
3.Gianluca M.A nonlinear elastic model for isotropic materials with different behavior in tension and compression // Transactions of the ASME — January 1982, № 104, 26 — 28 p.
4.Rigbi Z. Some thoughts concerning the existence or otherwise of an isotropic bimodulus material // ASME Journal of engineering materials and technology — October 1980, — № 102, 183—384 р.
отправлен участнику


Комментарии (5)
Оставить комментарий